НЬЮТОНА БИНОМ
НЬЮТОНА БИНОМ, название формулы, позволяющей выписывать разложение алгебраической суммы двух слагаемых произвольной степени. Впервые была предложена Ньютоном в 1664–1665:
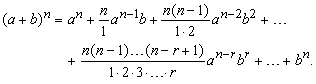
Коэффициенты формулы называются биномиальными коэффициентами. Если n – положительное целое число, то коэффициенты обращаются в нуль при любом r > n, поэтому разложение содержит лишь конечное число членов. Во всех остальных случаях разложение представляет собой бесконечный (биномиальный) ряд. (Условия сходимости биномиального ряда впервые были установлены в начале 19 в. Н.Абелем.) Такие частные случаи, как (a + b)2 = a2 + 2ab + b2 и (a + b)3 = a3 + 3a2b + 3ab2 + b3 были известны задолго до Ньютона.
Если n – положительное целое число, то биномиальный коэффициент при an – rbr в формуле бинома есть число комбинаций из n по r, обозначаемое Crn или (nr). При небольших значениях n коэффициенты можно найти из треугольника Паскаля:
| n = 0 |
1 |
||||||||
| n = 1 |
1 |
1 |
|||||||
| n = 2 |
1 |
2 |
1 |
||||||
| n = 3 |
1 |
3 |
3 |
1 |
|||||
| n = 4 |
1 |
4 |
6 |
4 |
1 |
||||
| и т.д. |
и т.д., |
||||||||
в котором каждое из чисел за исключением единиц равно сумме двух соседних чисел, стоящих строкой выше. Для данного n соответствующая (n-я) строка треугольника Паскаля дает по порядку коэффициенты биномиального разложения n-й степени, в чем нетрудно убедиться при n = 2 и n = 3.
См. также ВЕРОЯТНОСТЕЙ ТЕОРИЯ; РЯДЫ.
Ответь на вопросы викторины «Математика»