ЗЕНОН ЭЛЕЙСКИЙ

Содержание статьи

• Парадоксы множества.
• Парадоксы движения.
• Дихотомия.
• Ахилл.
• Стрела.
• Стадий.
• Другие парадоксы.
• Предикация.
• Место.

ЗЕНОН ЭЛЕЙСКИЙ – древнегреческий философ, представитель Элейской школы, ученик Парменида. Аристотель назвал Зенона создателем диалектики, искусства выдвигать аргументы и опровергать чужие мнения. Для защиты учения Парменида о едином неподвижном бытии Зенон сформулировал ряд апорий («неразрешимых положений»), показав, что признание реальности множественности и движения ведет к логическим противоречиям. Из четырех десятков апорий наиболее известны апории о движении: Дихотомия, Ахилл и черепаха, Стрела и Стадий (Движущиеся тела). Все эти апории представляют собой доказательства от противного. Вместе с вариантом их решения изложены у Аристотеля (Физика, VI, 9).

В первых двух (Дихотомия и Ахилл и черепаха) предполагается бесконечная делимость пространства. Так, как бы быстро ни бежал Ахилл, он никогда не догонит медленную черепаху, потому что за то время, которое ему потребуется для того, чтобы пробежать половину намеченного пути, черепаха, двигаясь без остановки, всегда будет отползать еще немного, и этот процесс не имеет завершения, ибо пространство делимо до бесконечности. В двух других апориях рассматривается несводимость непрерывности пространства и времени к неделимым «местам» и «моментам». Летящая стрела во всякий фиксируемый момент времени занимает определенное место, равное своей величине – получается, что в рамках самого неделимого момента она «покоится», и тогда получается, что движение стрелы состоит из суммы состояний покоя, что абсурдно. Следовательно, стрела на самом деле не движется. На протяжении всей дальнейшей истории апории Зенона являются предметом внимания и споров среди философов, логиков, математиков (Лейбниц, Кант, Коши, теория множеств Кантора).

Мария Солопова

Парадоксы множества.

Со времен Пифагора время и пространство рассматривались, с математической точки зрения, как составленные из множества точек и моментов. Однако они обладают также свойством, которое легче ощутить, нежели определить, а именно «непрерывностью». С помощью ряда парадоксов Зенон стремился доказать невозможность разделения непрерывности на точки или моменты. Его рассуждение сводится к следующему: предположим, что деление проведено нами до конца. Тогда верно одно из двух: либо мы имеем в остатке наименьшие возможные части или величины, которые неделимы, однако бесконечны по своему количеству, либо деление привело нас к частям, не имеющим величины, т.е. обратившимся в ничто, ибо непрерывность, будучи однородной, должна быть делимой повсюду, а не так, чтобы в одной своей части быть делимой, а в другой – нет. Однако оба результата нелепы: первый потому, что процесс деления нельзя считать законченным, пока в остатке – части, обладающие величиной, второй потому, что в таком случае изначальное целое было бы образовано из ничто. Симплиций приписывает это рассуждение Пармениду, однако кажется более вероятным, что оно принадлежит Зенону. Например, в Метафизике Аристотеля говорится: «Если единое само по себе неделимо, то по утверждению Зенона оно должно быть ничем, ибо он отрицает, чтобы то, что не увеличивается при прибавлении и не уменьшается при отнятии могло бы вообще существовать – разумеется, по той причине, что все существующее обладает пространственными размерами». В более полном виде этот довод против множественности неделимых величин приводит Филопон: «Зенон, поддерживая своего учителя, старался доказать, что все сущее должно быть единым и неподвижным. Доказательство свое он основывал на бесконечной делимости любой непрерывности. Именно, утверждал он, если сущее не будет единым и неделимым, но может делиться на множество, единого по сути вообще не будет (ибо если непрерывность можно делить, это будет означать, что ее можно делить до бесконечности), а если ничто не будет по сути единым, невозможно и множество, поскольку множество составлено из многих единиц. Итак, сущее не может быть разделено на множество, следовательно, есть только единое. Это доказательство может строиться и по-другому, а именно: если не будет сущего, которое неделимо и едино, не будет и множества, ибо множество состоит из многих единиц. А ведь каждая единица либо едина и неделима, либо сама делится на множество. Но если она едина и неделима, Вселенная составлена из неделимых величин, если же единицы сами подлежат делению, мы будем задавать тот же самый вопрос относительно каждой из подлежащих делению единиц, и так до бесконечности. Таким образом, если существующие вещи множественны, Вселенная окажется образованной бесконечным числом бесконечностей. Но поскольку этот вывод нелеп, сущее должно быть единым, а быть множественным ему невозможно, ведь тогда придется каждую единицу делить бесконечное число раз, что нелепо».

Симплиций приписывает Зенону несколько видоизмененный вариант того же аргумента: «Если множество существует, оно должно быть точно таким, каково оно есть, не больше и не меньше. Однако, если оно таково, каково есть, оно будет конечным. Но если множество существует, вещи бесконечны по числу, потому что между ними всегда будут обнаруживаться еще другие, а между теми еще и еще. Таким образом, вещи бесконечны по числу».

Рассуждения о множественности были направлены против соперничавшей с элеатами школы, вероятнее всего, против пифагорейцев, которые полагали, что величина или протяженность составлена из неделимых частей. Зенон считал, что эта школа полагает, будто непрерывные величины и до бесконечности делимы и конечным образом разделены. Предельные элементы, из которых, как предполагалось, состояло множество, имели, с одной стороны, свойства геометрической единицы – точки; с другой – они обладали некоторыми свойствами числового единства – числа. Подобно тому как из повторных прибавлений единицы строится числовой ряд, линия считалась составленной многократным прибавлением точки к точке. Аристотель приводит следующее пифагорейское определение точки: «Единица, имеющая положение» или «Единица, взятая в пространстве». Это означает, что пифагореизм усвоил своего рода числовой атомизм, с точки зрения которого геометрическое тело не отличается от физического. Парадоксы Зенона и открытие несоизмеримых геометрических величин (ок. 425 до н.э.) привели к возникновению непреодолимого разрыва между арифметической дискретностью и геометрической непрерывностью. В физике существовало два в чем-то аналогичных лагеря: атомисты, отрицавшие бесконечную делимость материи, и последователи Аристотеля, которые ее отстаивали. Аристотель вновь и вновь разрешает парадоксы Зенона как для геометрии, так и для физики, утверждая, что бесконечно малое существует лишь в потенции, но не в реальности. Для современной математики такой ответ неприемлем. Современный анализ бесконечности, в особенности в трудах Г.Кантора, привел к определению континуума, лишающему антиномии Зенона парадоксальности.

Парадоксы движения.

Значительная часть обширной литературы, посвященной Зенону, рассматривает его доказательства невозможности движения, поскольку именно в этой области воззрения элеатов вступают в противоречие со свидетельствами чувств. До нас дошли четыре доказательства невозможности движения, получившие названия «Дихотомия», «Ахилл», «Стрела» и «Стадий». Неизвестно, было ли их только четыре и в книге Зенона или же Аристотель, которому мы обязаны отчетливыми их формулировками, выбрал те, которые показались ему самыми трудными.

Дихотомия.

В первом парадоксе утверждается, что, прежде чем движущийся объект сможет преодолеть определенное расстояние, он должен пройти половину этого пути, затем половину оставшегося пути и т.д. до бесконечности. Поскольку при повторных делениях данного расстояния пополам всякий отрезок остается конечным, а число таких отрезков бесконечно, данный путь невозможно пройти за конечное время. Более того, этот довод действителен для любого, сколь угодно малого расстояния, и для любой, сколь угодно большой скорости. Следовательно, невозможно какое бы то ни было движение. Бегун не в состоянии даже тронуться с места. Симплиций, который подробно комментирует этот парадокс, указывает, что здесь за конечное время необходимо совершить бесконечное число касаний: «Тот, кто чего-либо касается, как бы считает, однако бесконечное множество невозможно сосчитать или перебрать». Или, как формулирует это Филопон, «бесконечное абсолютно неопределимо». Для того, чтобы пройти каждое из подразделений протяженности, с необходимостью требуется ограниченный временной интервал, но бесконечное число таких интервалов, как бы мал ни был каждый из них, в совокупности не может дать конечной длительности.

Аристотель усматривал в «дихотомии» скорее заблуждение, нежели парадокс, полагая, что его значимость сводится на нет «ложной посылкой.., будто невозможно пройти или коснуться бесконечного числа точек за конечный период времени». Также и Фемистий полагает, что «Зенон либо в самом деле не знает, либо делает вид, когда полагает, что ему удалось покончить с движением, сказав, что невозможно движущемуся телу за конечный период времени пройти бесконечное число положений». Аристотель считает точки лишь потенциальным, а не действительным бытием, временной или пространственный континуум «в реальности не делится до бесконечности», поскольку не такова его природа.

Ахилл.

Во втором парадоксе движения рассматривается состязание в беге между Ахиллом и черепахой, которой при старте дается фора. Парадокс заключается в том, что Ахилл никогда не догонит черепаху, поскольку сперва он должен добежать до того места, откуда начинает двигаться черепаха, а за это время она доберется до следующей точки и т.д., словом, черепаха всегда будет впереди. Разумеется, это рассуждение напоминает дихотомию с той только разницей, что здесь бесконечное деление идет сообразно прогрессии, а не регрессии. В «Дихотомии» доказывалось, что бегун не может пуститься в путь, потому что он не может покинуть того места, в котором находится, в «Ахилле» доказывается, что даже если бегуну удастся тронуться с места, он никуда не прибежит. Аристотель возражает, что бег – это не прерывный процесс, как толкует его Зенон, а непрерывный, однако этот ответ возвращает нас к вопросу, каково отношение дискретных положений Ахилла и черепахи к непрерывному целому? Современный подход к этой проблеме заключается в вычислениях (либо методом сходящихся бесконечных рядов, либо простым алгебраическим уравнением), которыми устанавливается, где и когда Ахилл нагонит черепаху. Предположим, Ахилл бежит в десять раз быстрее черепахи, которая проходит 1 м в секунду и имеет преимущество в 100 м. Пусть х – расстояние в метрах, пройденное черепахой к тому моменту, когда Ахилл ее нагонит, а t – время в секундах. Тогда t = x/1 = (100+x)/10 = 11 ¹/₉ с. Вычисления показывают, что бесконечному количеству движений, которые должен совершить Ахилл, соответствует конечный отрезок пространства и времени. Однако самими по себе вычислениями парадокс не разрешается. Ведь сначала необходимо доказать утверждение, что расстояние – это скорость, умноженная на время, а сделать это невозможно без анализа того, что подразумевается под моментальной скоростью – понятием, лежащим в основе третьего парадокса движения.

В большинстве источников, где излагаются парадоксы, говорится о том, что Зенон вообще отрицал возможность движения, но иногда утверждается, что доводы, которые он отстаивал, были направлены лишь на доказательство несовместимости движения с постоянно оспаривавшимся им представлением о непрерывности как о множестве. В «Дихотомии» и «Ахилле» утверждается, что движение невозможно при предположении о бесконечной делимости пространства на точки, а времени на мгновения. В последних двух парадоксах движения утверждается, что движение равным образом невозможно и в том случае, когда делается противоположное предположение, а именно, что деление времени и пространства завершается неделимыми единицами, т.е. время и пространство обладают атомарной структурой.

Стрела.

Согласно Аристотелю, в третьем парадоксе – о летящей стреле – Зенон утверждает: любая вещь либо движется, либо стоит на месте. Однако ничто не может пребывать в движении, занимая пространство, которое равно ему по протяженности. В определенный момент движущееся тело (в данном случае стрела) постоянно находится на одном месте. Следовательно, летящая стрела не движется. Симплиций формулирует парадокс в сжатой форме: «Летящий предмет всегда занимает пространство, равное себе, но то, что всегда занимает равное себе пространство, не движется. Следовательно, оно покоится». Филопон и Фемистий дают близкие к этому варианты.

Аристотель с наскока отмел парадокс «стрела», утверждая, что время не состоит из неделимых моментов. «Ошибочен ход рассуждений Зенона, когда он утверждает, что если все, занимающее равное себе место, находится в покое, и то, что находится в движении, всегда занимает в любой момент такое место, то летящая стрела окажется неподвижной». Трудность устраняется, если вместе с Зеноном подчеркнуть, что в каждый данный момент времени летящая стрела находится там, где она находится, все равно как если бы она покоилась. Динамика не нуждается в понятии «состояния движения» в аристотелевском смысле, как реализации потенции, однако это не обязательно должно приводить к сделанному Зеноном выводу, что раз такой вещи, как «состояние движения», не существует, не существует и самого движения, стрела неизбежно находится в покое.

Стадий.

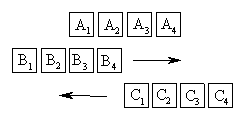
Больше всего споров вызывает последний парадокс, известный под названием «стадий», и он же труднее прочих поддается изложению. Тот его вид, в котором он дан Аристотелем и Симплицием, отличается фрагментарностью, и соответствующие тексты считаются не вполне надежными. Возможная реконструкция данного рассуждения имеет следующий вид. Пусть А₁, А₂, А₃ и А₄ – неподвижные тела равного размера, а В₁, В₂, В₃ и В₄ – тела, имеющие такой же размер, что и А, которые единообразно движутся вправо так, что каждое В минует каждое А за одно мгновение, считая мгновение наименьшим возможным промежутком времени. Пусть С₁, С₂, С₃ и С₄ – тела также равного А и В размера, которые единообразно движутся относительно А влево так, что каждое С проходит мимо каждого А тоже за мгновение. Предположим, что в определенный момент времени эти тела находятся в следующем положении друг относительно друга:

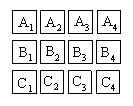
Тогда через два мгновения позиция станет следующей:

Отсюда очевидно, что С₁ миновало все четыре тела В. Время, которое потребовалось С₁ для прохождения одного из тел В, можно принять за единицу времени. В таком случае на все передвижение потребовалось четыре такие единицы. Однако предполагалось, что два момента, которые прошли за это передвижение, являются минимальными и потому неделимыми. Из этого с необходимостью следует, что две неделимые единицы равны четырем неделимым единицам.

Согласно некоторым толкованиям «стадия», Аристотель полагал, что Зенон совершил здесь элементарную ошибку, предположив, что телу требуется одно и то же время на прохождение мимо подвижного тела и тела неподвижного. Эвдем и Симплиций также интерпретируют «стадий» как всего лишь смешение абсолютного и относительного движения. Но если бы это было так, парадокс не заслуживал бы того внимания, которое уделил ему Аристотель. Поэтому современные комментаторы признают, что Зенон видел здесь более глубокую проблему, затрагивающую структуру непрерывности.

Другие парадоксы.

Предикация.

К числу более сомнительных парадоксов, приписываемых Зенону, относится рассуждение о предикации. В нем Зенон утверждает, что вещь не может в одно и то же время быть единой и иметь множество предикатов; таким же точно доводом пользовались афинские софисты. В Пармениде Платона это рассуждение выглядит так: «Если вещи множественны, они должны быть и подобными, и неподобными [неподобными, поскольку они не являются одним и тем же, и подобными, поскольку общее у них то, что они не являются одним и тем же]. Однако это невозможно, поскольку неподобные вещи не могут быть подобными, а подобные неподобными. Следовательно, вещи не могут быть множественны».

Здесь мы вновь видим критику множественности и столь характерный косвенный тип доказательства, и потому этот парадокс был также приписан Зенону.

Место.

Аристотель приписывает Зенону парадокс «Место», похожие рассуждения приводят Симплиций и Филопон в 6 в. н.э. В Физике Аристотеля эта проблема излагается следующим образом: «Далее, если существует место само по себе, где оно находится? Ведь затруднение, к которому приходит Зенон, нуждается в каком-то объяснении. Поскольку все, что существует, имеет место, очевидно, что место тоже должно иметь место и т.д. до бесконечности». Считается, что парадокс возникает здесь потому, что ничто не может содержаться само в себе или отличаться от самого себя. Филопон добавляет, что, показав самопротиворечивость понятия «места», Зенон желал доказать несостоятельность концепции множественности.