МАГНИТНАЯ ГИДРОДИНАМИКА (МГД)

Содержание статьи

• Силы, действующие на электропроводные жидкости и газы.
• Уравнения Максвелла и обобщенный закон Ома.
• Уравнение индукции магнитного поля. Магнитное число Рейнольдса.
• Уравнения идеальной магнитной гидродинамики.
• Течение Гартмана.

МАГНИТНАЯ ГИДРОДИНАМИКА (МГД) – наука, изучающая движение электропроводных жидкостей и газов. Математическим аппаратом МГД являются уравнения гидроаэромеханики и уравнения Максвелла для электромагнитных величин. В ряде областей физики, механики, техники возникает необходимость изучения движений электропроводных жидкостей и газов. К таким областям, например, относятся астрофизика, аэродинамика больших скоростей, магнитогидродинамические генераторы электрической энергии, электромагнитные насосы для перекачки жидких металлов, плазменные ускорители, управляемые термоядерные реакции и т.п. Если предметом изучения является газ, то свойством проводника электричества он обладает только тогда, когда находится в ионизованном состоянии. Например, воздух при атмосферном давлении обладает этими свойствами при температуре Т і 5000К.

Ионизованный газ чаще всего называют плазмой, если он обладает в среднем свойством квазинейтральности, т.е. свойством, при котором положительные заряды почти компенсируются отрицательными. Если плазму поместить в электромагнитное поле, то в ней появляются электрические токи, которые, в свою очередь, приводят к появлению электромагнитной силы, воздействующей на ее движение. Из школьных учебников известно, что при протекании электрического тока по проводнику создается собственное магнитное поле, которое искажает внешнее (наложенное на проводник) магнитное поле. В рассматриваемом случае, когда таким проводником являются жидкие металлы или ионизованный газ, это означает, что не только электромагнитные силы оказывает воздействие на их движение, но и движение таких сред воздействуют на электромагнитное поле. Возникает сложное взаимодействие между электропроводными жидкостями и газами и электромагнитным полем. Математически это означает, что в рамках модели сплошной среды (См. также ГИДРОАЭРОМЕХАНИКА) возникает сложная проблема совместного решения системы уравнений гидроаэромеханики и уравнений Максвелла для электромагнитного поля.

Силы, действующие на электропроводные жидкости и газы.

Чтобы жидкости или газы были проводниками электричества, в них должны присутствовать свободные заряженные частицы, например, полностью ионизованный водород состоит только из свободных протонов и электронов.

Пусть электромагнитное поле характеризуется вектором напряженности электрического поля E и вектором магнитной индукции B. В электродинамике обычно вводят еще вектор электрической индукции D и вектор напряженности магнитного поля H. Ниже (можно ограничиться первыми двумя векторами, поскольку в магнитной гидродинамике различие между E и D, а также между B и H несущественно).

На отдельную частицу с зарядом e_k, движущуюся со скоростью v_k, в электромагнитном поле Е, В действует сила, равная

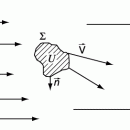
, где с – скорость света, характеризующая абсолютную гауссовскую систему единиц измерения, в которой векторы напряженности электрического поля и магнитной индукции имеют одинаковую размерность, а квадрат магнитного поля имеет размерность гидростатического давления в гидроаэромеханике.Для вычисления силы rF, которая действует на единицу объема электропроводной жидкости или газа в присутствии электромагнитной силы, суммируются силы, действующие на одну частицу, по всем частицам, находящимся в элементе физического объема DU. В результате электромагнитная сила, действующая на единицу объема сплошной среды, может быть записана в виде

, где

Здесь r_е – плотностью заряд, и j – вектор плотности электрического тока. Суммирование в последних соотношениях идет по сортам частиц, а не по всем частицам, поскольку многие частицы сплошной среды являются одинаковыми. При этом n₂₂₆ и V₂₂₆ – концентрация (число частиц в единице объема) и вектор средней скорости частиц сорта a соответственно. Так, например, для полностью ионизованного атомарного водорода

,

Здесь индексы «p» и «е» относятся к протонам и электронам соответственно, а абсолютная величина заряда электрона равна е = е_p = –e_e = 4,8 ·10^–10 (г^1/2cм^3/2сек^–1).

Таким образом, электропроводные среды состоят, как минимум, из двух сортов частиц. Обычно для описания движения таких сред, как целое, используется прием, связанный с суммированием уравнений механики сплошных сред по сортам a отдельного континуума. Для феноменологического вывода уравнений магнитной гидродинамики можно воспользоваться законами сохранения массы, импульса и энергии в интегральном виде как для разрывных, так и для непрерывных функций, как это обычно делается в гидроаэромеханике. Отличие состоит только в том, что в закон сохранения импульса необходимо добавить массовую силу электромагнитного происхождения, а в закон сохранения энергии – выделение тепла за счет протекания электрического тока, обычно называемое джоулевым теплом. При этом для массовой силы обычно выполняется неравенство |r_еЕ| << | 1/c j×B|, поскольку плотность электрического заряда в силу квазинейтральности очень мала, хотя и не равна точно нулю. Таким образом в магнитной гидродинамике часть силы, связанная с электрическим полем, очень мала и ею можно пренебречь.

Уравнения гидроаэромеханики для электропроводных жидкостей и газов.

Можно выписать основные уравнения гидрофэромеханики для электропроводных жидкостей и газов в присутствии электрического и магнитного полей. Уравнение неразрывности имеет тот же вид, что и в гидроаэромеханике, а именно

Однако в этом уравнении массовая плотность r и средняя скорость V определяются по формулам

Здесь m₂₂₆ – масса частицы сорта a (суммирование происходит по всем сортам частиц).

Закон сохранения импульса в дифференциальной форме принимает вид (электрической силой можно пренебречь)

где последний член справа представляет собой массовую силу, связанную с протеканием электрического тока через проводящую среду, силы вязкости записаны в упрощенном виде для несжимаемой жидкости. Это уравнение в гидроаэромеханике обычно называется уравнением движения.

Уравнение притока тепла, которое получается из закона сохранения энергии, в рассматриваемом случае электропроводной жидкости или газа имеет вид

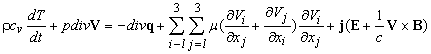
Здесь предполагается, что вектор потока тепла q определяется законом Фурье, температуры всех компонент одинаковы и добавлен последний член справа, связанный с выделением тепла вследствие протекания электрических токов. Через V_iобозначены компоненты вектора скорости.

Выписанные выше уравнения неразрывности, движения и притока тепла вместе с уравнением состояния для идеального газа и законом Фурье для вектора потока тепла соответственно

p = rRT, q = –lСT

была бы замкнутой системой для определения плотности r, скорости V, давления р и температуры Т, если бы были известны величины, связанные с электромагнитным полем E, B и j. Однако протекание электрического тока по проводнику создает собственное магнитное поле, которое, вообще говоря, изменяет поле, приложенное извне. Это означает, что величины Е, В и j в общем случае заранее не известны, а, следовательно, написанная система уравнений не является замкнутой. Физически это означает, что есть взаимное влияние электромагнитного поля на движение электропроводных жидкостей или газов также как и движения среды на электромагнитное поле. Чтобы замкнуть систему уравнений, нужно добавить уравнения электродинамики.

Уравнения Максвелла и обобщенный закон Ома.

Уравнения

div B = 0, div E = 4pr_e,

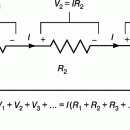
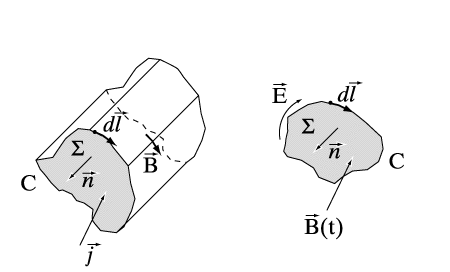
выражающие собой отсутствие магнитных зарядов и возникновение электрического поля вследствие присутствия электрических зарядов соответственно, были известны задолго до опытов Фарадея (1831), установившего связь между электрическим и магнитным полями (законы индукции Фарадея). В своих опытах Фарадей установил, что при протекании по проводнику с площадью поперечного сечения S электрического тока (см. Рис.1) Возникает циркуляция вектора индукции магнитного поля по контуру С, ограничивающему площадь S, а изменение со временем потока магнитного поля через площадь S создает в контуре С циркуляцию вектора напряженности электрического поля. В интегральной форме результаты этих опытов можно записать соответственно в виде

Здесь dl – элемент дуги вдоль контура С, а n – вектор нормали к поверхности S (конечно, во времена Фарадея еще не было векторного анализа, который позволяет записать эти соотношения в компактной векторной форме). Если подынтегральные функции в последних соотношениях непрерывны, то после перехода от контурных интегралов к поверхностным и приравнивания подынтегральных выражений, можно получить дифференциальные уравнения, определяющие законы индукции Фарадея для электромагнитных величин, в виде

где оператор rot, примененный к произвольному вектору А, в декартовой системе координат имеет проекции на оси Ox, Oy и Oz соответственно

При написании этих уравнений использовалась гауссовская система единиц измерения электромагнитных величин, в которой имеют место следующие размерности

[E] = [В] = [г^1/2см^–1/2сек^–1], [j] = [г^1/2см^–1/2сек^–2].

Более чем через тридцать лет после открытия законов индукции Фарадеем великий английский ученый Дж.Максвелл заметил противоречие в этих законах. А именно, из первого уравнения следует (в векторном анализе есть тождество div (rot) є 0), что

div j = 0.

Используя уравнение неразрывности для каждой компоненты

справедливое при отсутствии химических реакций между компонентами, умножая это уравнение на заряд е_a, суммируя по a и пользуясь определениями r_е и j, можно получить

Сравнивая два последних уравнения для плотности тока j, можно видеть, что они противоречивы, и это привело Максвелла к идее исправить законы индукции Фарадея и записать их в виде

Из первого уравнения с использованием уравнения divE = 4pr_e легко показать, что противоречие в законах индукции Фарадея устраняется. Введенный в первое уравнение Максвеллом член ¶Е/¶t получил название тока смещения (в отличие от первого члена справа, названного током проводимости). Эти уравнения получили название уравнений Максвелла.

Следует заметить, что ток смещения в проводниках обычно очень мал по сравнению с током проводимости и именно это обстоятельство привело к тому, что Фарадей не смог обнаружить их в опытах, а поэтому и не включил его в свои законы индукции. Однако введение тока смещения предсказало возможность распространения электромагнитных волн в ваакуме (при j = 0 из последних уравнений легко получить волновое уравнение для B или Е), что привело к революционному перевороту, связанному с передачей информации на большие расстояния.

Можно показать, что в электропроводных жидкостях или газах токи смещения очень малы. Поэтому в магнитной гидродинамике ими можно пренебречь, а к системе уравнений гидроаэромеханики добавляются более простые законы индукции Фарадея. Однако последние два уравнения не являются замкнутой системой уравнений для векторов Е и В, если плотность тока j не связать с этими векторами. Как известно из электротехники, в неподвижных проводниках имеет место закон Ома

j = sE,

т.е. плотность тока пропорциональна напряженности электрического поля (s – электропроводность среды). В классической магнитной гидродинамике, основанной лауреатом Нобелевской премии, шведским физиком и астрофизиком Х.Альфвеном, для замыкания системы уравнений магнитной гидродинамики выводится обобщенный закон Ома для подвижных проводников.

В системе координат, движущейся с элементом электропроводной жидкости со скоростью V, закон Ома имеет тот же вид, что и для неподвижных проводников

j¹⁸¹ = sE¹⁸¹,

где штрихи означают соответствующий вектор в системе координат, движущейся со скоростью V. При условии, что скорость этой системы координат нерелятивистская (много меньше скорости света) и при условии квазинейтральности, преобразования Лоренца для электромагнитных величин имеют вид

Подставив эти соотношения в последнее уравнение, можно получить обобщенный закон Ома в форме

В результате система уравнений, состоящая из уравнения неразрывности, движения, притока тепла, уравнения состояния, закона Фурье, законов индукции Фарадея, обобщенного закона Ома и уравнений для вектора индукции магнитного поля divВ = 0, становится замкнутой системой дифференциальных уравнений магнитной гидродинамики для определения r, V, p, T, E, B и j. Интересно, что при использовании обобщенного закона Ома последний член в правой части уравнения притока тепла принимает вид j² / s, который хорошо известен в электротехнике для неподвижных проводников как выделение джоулева тепла.

Плотность заряда r_е входит только в уравнение divE = 4pr_e. Это означает, что в замкнутую систему уравнений магнитной гидродинамики это уравнение не входит, поскольку из него отдельно можно определить распределение плотности заряда после определения всехостальных магнитогидродинамических параметров. Именно в этом смысле нужно понимать понятие квазинейтральности, при которой, вообще говоря, r_е№ 0, хотя члены с плотностью заряда, входящие в другие уравнения магнитной гидродинамики, пренебрежимо малы.

Уравнение индукции магнитного поля. Магнитное число Рейнольдса.

Система уравнений магнитной гидродинамики может быть упрощена,если исключить из нее плотность тока j и вектор напряженности электрического поля Е при помощи законов индукции Фарадея. Кроме того, взяв операцию «rot» от обобщенного закона Ома, воспользовавшись векторным тождеством «rot(rot) = Сdiv – D» и уравнением div B = 0, при постоянной электропроводности s можно получить уравнение

которое называется уравнением индукции магнитного поля. Вместе с уравнением неразрывности, уравнением движения, записанным в форме

уравнением притока тепла в виде

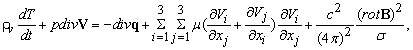а также уравнением состояния, законом Фурье (q = –lСT) и уравнением div B = 0 они представляют собой замкнутую систему уравнений магнитной гидродинамики для определения r, V, р, Т и В. Эти уравнения учитывают диссипативные процессы, связанные с вязкостью, теплопроводностью и выделением тепла из-за протекания электрических токов.

Уравнение индукции магнитного поля имеет очень важную интерпретацию в магнитной гидродинамике. Действительно, отношение по порядку величины второго члена в правой стороне этого уравнения к первому равно

Здесь V – некоторая характерная скорость задачи (например, скорость невозмущенного потока, набегающего на обтекаемое тело), а L – характерный размер (например, размер обтекаемого тела). Величина n_m называется магнитной вязкостью. Число Re_m внешне похоже на число Рейнольдса в классической гидроаэромеханике (только вместо кинематической вязкости жидкости n = m /r в рассматриваемом случае в знаменателе стоит магнитная вязкость) и играет такую же важную роль как и число Рейнольдса в гидроаэромеханике.

Предельные случаи:

(а) Re_m >>1 и (б) Re_m<<1.

В первом случае очень больших магнитных чисел Рейнольдса уравнение индукции магнитного поля можно записать в форме

в которой пренебречь последним членом полного уравнения, представляющим собой диссипацию энергии вследствие протекания электрических токов. Из последнего уравнения видно, что движение электропроводных жидкостей и газов в случае (а) сильно влияет на распределение магнитного поля, а, следовательно, и на распределение всех остальных электродинамических величин. Кроме того, есть теорема, что поток соленоидального вектора, которым является магнитное поле (div B = 0), через некоторую поверхность S в жидкости, ограниченную жидким контуром С, остается со временем постоянным. Физически это означает, что никакая силовая линия магнитного поля во время движенния не может покинуть поверхность S через контур С. Это свойство электропроводных жидкостей и газов в случае (а) называется условием «вмороженности» магнитных силовых линий в электропроводную среду. В гидроаэромеханике аналогом являются вихревые линии, которые при некоторых условиях могут быть «вморожены» в жидкость (одна из теорем Гельмгольца о вихрях). Случай (а) чаще всего осуществляется в различных физических проблемах, встречающихся в условиях космического пространства. Это связано с тем, что обычно в этих условиях характерные размеры L приводят к очень большим значениям магнитного числа Рейнольдса.

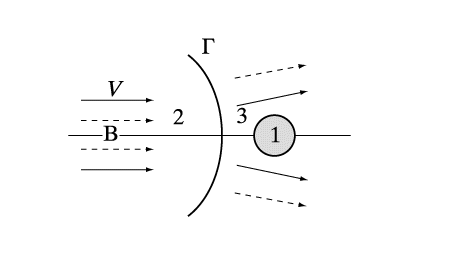
В качестве примера приведем обтекание магнитосферы Земли солнечным ветром. Скорость солнечного ветра в районе орбиты Земли равна, в среднем, V ~ 4·10⁷см/сек, характерный размер обтекаемой магнитосферы L ~ 10R_E ~ 6,4·10⁹ см (R_E – радиус Земли), n _m ~ 10⁶ см²/сек, т.е. Re_m~ 10¹¹>>1. Таким образом, при обтекании Земли солнечным ветром осуществляется случай (а), т.е., в силу принципа «вмороженности», солнечный ветер не может проникнуть в магнитосферу Земли, а обтекает ее, поджимая магнитосферу с подветренной стороны и вытягивая ее в хвостовой части, как показано на рис. 2. На этом рисунке область «1» представляет собой невозмущенный солнечный ветер, Г – головная ударная волна, М – так называемая магнитопауза, отделяющая солнечный ветер за головной ударной волной от магнитосферы Земли, А – точка торможения солнечного ветра, в которой скорость равна нулю, область «2» заполнена солнечным ветром, параметры которого за ударной волной отличаются от параметров в области «1», область «3» – магнитосфера Земли, куда не проникает солнечный ветер. Исследования с помощью космических аппаратов обнаружили, что хвост магнитосферы Земли может вытягиваться вплоть до орбиты Луны.

В случае (б) уравнение индукции имеет вид

Из этого уравнения видно, что движение электропроводных жидкостей и газов не влияет на магнитное поле, а, следовательно, и на другие электродинамические величины. В этом случае малых магнитных чисел Рейнольдса, который обычно встречается в лабораторных условиях из-за небольших электропроводностей и малых характерных масштабов рассматриваемых проблем, электрическое и магнитное поля можно считать заданными величинами и не рассматривать законы индукции Фарадея. Математическая задача решения таких проблем, к которым относятся плазменные ускорители, магнитогидродинамические генераторы энергии, электромагнитные насосы для перекачки жидких металлов и т.п., существенно упрощается.

В качестве примера рассмотрим основной принцип устройства магнитогидродинамического генератора. По каналу, например, прямоугольного сечения вдоль оси Оx пропускается электропроводная жидкость со скоростью U в магнитном поле B, направленном вдоль оси Oz, перпендикулярной плоскости чертежа (см. рис. 3). Тогда, в силу обобщенного закона Ома, перпендикулярно скорости течения и магнитному полю (эффективное электрическое поле равно 1/c V ґ B) вдоль оси Oy потечет электрический ток. Если бы стенки канала 1 и 2 были диэлектриками, то возникло бы электрическое поле Е, которое привело бы к запиранию тока (Е = –1/c V ґ B, т.е. j = 0). Однако, если 1 и 2 являются электродами, то по показанной на рис. 3 замкнутой электрической цепи потечет ток, который может быть измерен амперметром А. На таком принципе и устроены магнитогидродинамические генераторы. При этом массовая сила в уравнении движения, пропорциональная векторному произведению j ґ B, направлена противоположно скорости и будет тормозить поток.

Можно видеть, что при внешнем воздействии электрического поля, перпендикулярного внешнему приложенному магнитному полю, можно добиться, чтобы сила 1/c j ґ B действовала вдоль направления скорости. На таком принципе основаны плазменные ускорители.

Уравнения идеальной магнитной гидродинамики.

Если в уравнениях магнитной гидродинамики пренебречь диссипативными процессами (вязкостью, теплопроводностью и джоулевыми потерями), то можно получить систему уравнений идеальной магнитной гидродинамики. Замкнутая система таких уравнений имеет вид:

– уравнение неразрывности,

– уравнение движения,

– адиабатический закон,

– уравнение индукции магнитного поля,

– условие замкнутости магнитных силовых линий или их бесконечности (условие отсутствия магнитных зарядов).

Здесь, как и в гидпроаэромеханике, введена полная производная по времени, которая в декартовой системе координат будет иметь вид

где u, n и w – компоненты скорости вдоль осей Ox, Oy и Oz соответственно.

Эта система уравнений служит для определения r, V, p и B. На ее основе можно найти скорость распространения малых возмущений. В гидроаэромеханике известно, что скорость распространения малых возмущений в идеальном газе равна скорости звука a₀, определяемой формулой

где индекс «0» здесь и ниже относится к невозмущенным параметрам газа, g = с_p/c_v – показатель адиабаты, c_p, c_v – удельные теплоемкости при постоянном давлении и объеме соответственно, R = c_p – c_v – газовая постоянная.

При наличии магнитного поля в идеальном электропроводном газе можно показать, что малые возмущения могут распространятся по газу с тремя возможными скоростями: с быстрой магнитозвуковой скоростью, медленной и альфвеновской, которые определяются соответственно

и

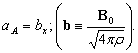
В этих формулах система координат выбрана таким образом, что малые возмущения распространяются вдоль оси Ox. Те же величины с обратным знаком определяют скорости волн, распространяющихся в отрицательную сторону оси Ox. Из этих выражений видно, что в отсутствие магнитного поля (при В = 0) остается только скорость звука в гидроаэромеханике. В общем случае альфвеновская скорость по величине лежит между быстрой и медленной магнитозвуковыми скоростями. Наличие трех скоростей распространения малых возмущений допускает в магнитной гидродинамике решение, связанное со сверхзвуковым обтеканием тел, при котором образуются головные ударные волны, направленные вверх по потоку (см. рис. 4), что невозможно в гидроаэромеханике. Однако присутствие таких ударных волн пока в природе не обнаружено.

Физический смысл альфвеновской скорости легко понять на примере несжимаемой жидкости (r = const), для которой уравнение неразрывности имеет вид

div V = 0.

В этом случае для одномерных нестационарных течений (зависящих только от координаты x и времени t) уравнения движения и магнитной индукции для идеальной жидкости можно свести к двум уравнениям

где введены векторы магнитной индукции B_i и скорости V_i , перпендикулярные оси Ox, т.е. они имеют компоненты (B_y, B_z) и (v, w) соответственно. Из двух последних уравнений легко получить волновое уравнение либо для B_i , либо для V_i (B_x0 = const, u = 0). Например, для B_i имеем

Общее решение этого волнового уравнения записывается в виде

Аналогичное решение получается и для V_i . Видно, что решением магнитогидродинамических уравнений для идеальной и несжимаемой жидкости являются волны, которые могут распространяться в обе стороны оси Ox со скоростью V_A. Такие волны называются волнами Альфвена. Они являются поперечными волнами в том смысле, что распространяются вдоль оси Ox, но колебания скорости и магнитного поля испытывают только их поперечные компоненты. Альфвеновские волны встречаются в природе, например, они часто наблюдаются с помощью космических аппаратов в межпланетной среде, как ее малые возмущения, хотя для несжимаемой жидкости решения для таких волн, выписанные выше, получены без предположения о малости их амплитуды.

Течение Гартмана.

Уравнения магнитной гидродинамики имеют решение, описывающее течение вязкой электропроводной несжимаемой жидкости в канале при наличии поперечного магнитного поля. Такое течение является обобщением течения Пуазейля в обычной гидроаэромеханике и называется течением Гартмана.

Пусть есть течение в плоском канале прямоугольного сечения, в котором расстояние между стенками, параллельными плоскости Oxz (рис. 5), много меньше расстояния между стенками, параллельными плоскости Oyz. Канал предполагается бесконечным вдоль оси Oz, скорость имеет только одну компоненту w, направленную вдоль этой оси, а наложенное на течение постоянное магнитное поле направлено вдоль оси Oy. Жидкость движется в канале под действием постоянного перепада давления P = –¶p/¶z.

При такой постановке задачи фактически рассматривается течение, при котором в стационарном случае скорость жидкости, в силу эффектов вязкости, зависит только от координаты y. Если боковые стенки канала – электроды, то, как видно из рассмотрения принципиальной схемы магнитогидродинамического генератора, вдоль оси Ox, перпендикулярной плоскости течения, потечет электрический ток. При этом появляется индуцированное магнитное поле с компонентой B_z, зависящей также только от координаты y, в отличие от постоянного приложенного магнитного поля, направленного вдоль оси Oy. Уравнение движения в этом случае имеет вид

а уравнение индукции магнитного поля –

В качестве граничных условий используются условия прилипания жидкости на стенках канала и равенство них нулю индуцированной компоненты магнитного поля, т.е.

w = 0, B_z = 0 при y = ± a.

При этих граничных условиях можно получить точное решение

где w₀ – максимальная скорость потока в центре канала (при y = 0), которая, конечно, зависит от перепада давления Р, а величина d определяется формулой и определяет так называемое число Гартмана . Физически квадрат числа Гартмана по порядку величины определяет отношение электромагнитной силы к1/c jґB к= к1/c²s VґBкк силам вязкости кmDV к. Чем меньше число Гартмана, т.е. чем меньше электромагнитная сила, тем больше приведенный выше профиль скорости должен приближаться к параболическому профилю течения Пуазейля. Действительно, легко показать, что предел для полученной скорости течения w при наличии поперечного магнитного поля при На ® 0 равен

w = w₀ (1 – y²/a²),

т.е. в предельном случае получается профиль Пуазейля для плоского канала. Очевидно, что из-за тормозящей силы, связанной с магнитным полем, расход жидкости через канал в единицу времени при одинаковом перепаде давления Р будет меньше, чем при течении Пуазейля. Кроме того, в магнитном поле профиль скорости становится более плоским: у стенок градиент скорости возрастает, а вблизи центра канала уменьшается. Первое обстоятельство приводит к увеличению сопротивления канала течению жидкости из-за вязкого трения.

Области применения сравнительно молодой науки магнитной гидродинамики обширны. Особую роль магнитная гидродинамика играет в астрофизике, поскольку Вселенная на 90% состоит из ионизованного газа, находящегося в электромагнитном поле. Примеры магнитогидродинамических генераторов энергии, плазменных ускорителей, насосов для перекачки жидких металлов, проблем, связанных с управляемыми термоядерными реакциями, и т.п. указывают на то, что основы МГД важны и в земных условиях.

Тем не менее эта наука непрерывно развивается, поскольку в своей классической формеона имеет много ограничений, которые приводят к невозможности ее использования во многих задачах, связанных с движением электропроводных сред. Интересно, что создатель магнитной гидродинамики Х. Альфвен, получивший за это Нобелевскую премию, резко раскритиковал свое детище в торжественной Нобелевской речи. Он отметил, что в природе часто случаются ситуации, в которых электрическое поле имеет компоненту вдоль магнитного поля, что противоречит разобранному выше условию «вмороженности» магнитного поля в жидкость. Кроме того, в условиях космоса часто бывает неизвестным выбор характерного размера задачи, который входит в определение важного в теории магнитного числа Рейнольдса.

Классическая магнитная гидродинамика не учитывает важные эффекты вращения заряженных частиц в магнитном поле. Такое вращение приводит к образованию токов Холла, не учитываемых в приведенной форме обобщенного закона Ома, к анизотропии вязкости и теплопроводности (коэффициенты m и l различны вдоль магнитного поля и в поперечном к нему направлении) и к другим эффектам. Эти эффекты не являются обычно существенными в плотных газах, характерных для земных условий, но очень важны в разреженных средах, наиболее часто встречающихся в астрофизических приложениях.

Владимир Баранов