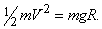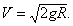ОРБИТА
ОРБИТА, в астрономии, – путь небесного тела в пространстве. Хотя орбитой можно называть траекторию любого тела, обычно имеют в виду относительное движение взаимодействующих между собой тел: например, орбиты планет вокруг Солнца, спутников вокруг планеты или звезд в сложной звездной системе относительно общего центра масс. Искусственный спутник «выходит на орбиту», когда начинает двигаться по циклической траектории вокруг Земли или Солнца. Термин «орбита» используется также в атомной физике при описании электронных конфигураций. См. также АТОМ.
Абсолютные и относительные орбиты.
Абсолютной орбитой называют путь тела в системе отсчета, которую в каком-то смысле можно считать универсальной и потому абсолютной. Такой системой считают Вселенную в большом масштабе, взятую как целое, и называют ее «инерциальной системой». Относительной орбитой называют путь тела в такой системе отсчета, которая сама движется по абсолютной орбите (по искривленной траектории с переменной скоростью). Например, у орбиты искусственного спутника обычно указывают размер, форму и ориентацию относительно Земли. В первом приближении это эллипс, в фокусе которого находится Земля, а плоскость неподвижна относительно звезд. Очевидно, это относительная орбита, поскольку она определена по отношению к Земле, которая сама движется вокруг Солнца. Удаленный наблюдатель скажет, что спутник движется относительно звезд по сложной винтовой траектории; это его абсолютная орбита. Ясно, что форма орбиты зависит от движения системы отсчета наблюдателя.
Необходимость различать абсолютную и относительную орбиты возникает потому, что законы Ньютона верны только в инерциальной системе отсчета, поэтому их можно использовать только для абсолютных орбит. Однако мы всегда имеем дело с относительными орбитами небесных тел, ибо наблюдаем их движение с обращающейся вокруг Солнца и вращающейся Земли. Но если абсолютная орбита земного наблюдателя известна, то можно либо перевести все относительные орбиты в абсолютные, либо представить законы Ньютона уравнениями, верными в системе отсчета Земли.
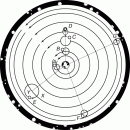
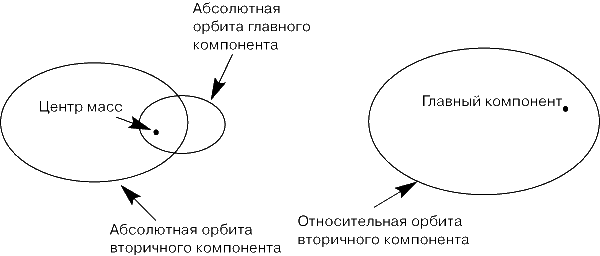
Абсолютную и относительную орбиты можно проиллюстрировать на примере двойной звезды. Например, Сириус, кажущийся невооруженному глазу одиночной звездой, при наблюдении с большим телескопом оказывается парой звезд. Путь каждой из них можно проследить отдельно по отношению к соседним звездам (принимая во внимание, что и сами они движутся). Наблюдения показали, что две звезды не только обращаются одна вокруг другой, но и перемещаются в пространстве так, что между ними всегда есть точка, движущаяся по прямой линии с постоянной скоростью (рис. 1). Эту точку называют центром масс системы. Практически с ней связана инерциальная система отсчета, а траектории звезд относительно нее представляют их абсолютные орбиты. Чем дальше отходит звезда от центра масс, тем она легче. Знание абсолютных орбит позволило астрономам вычислить по отдельности массы Сириуса А и Сириуса В.
Если же измерять положение Сириуса В относительно Сириуса А, то получим относительную орбиту (рис. 2). Расстояние между этими двумя звездами всегда равно сумме их расстояний от центра масс, поэтому относительная орбита имеет ту же форму, что и абсолютные, а по размеру равна их сумме. Зная размер относительной орбиты и период обращения, можно, используя третий закон Кеплера, вычислить лишь суммарную массу звезд. См. также НЕБЕСНАЯ МЕХАНИКА.
Более сложный пример представляет движение Земли, Луны и Солнца. Каждое из этих тел движется по своей абсолютной орбите относительно общего центра масс. Но поскольку Солнце значительно превосходит всех по массе, принято изображать Луну и Землю в виде пары, центр масс которой движется по относительной эллиптической орбите вокруг Солнца. Однако эта относительная орбита весьма близка к абсолютной. См. также ЛУНА.
Движение Земли относительно центра масс системы Земля – Луна наиболее точно измеряется с помощью радиотелескопов, определяющих расстояние до межпланетных станций. В 1971 при полете аппарата «Маринер-9» к Марсу по периодическим вариациям расстояния до него определили амплитуду движения Земли с точностью 20–30 м. Центр масс системы Земля – Луна лежит внутри Земли, на 1700 км ниже ее поверхности, а отношение масс Земли и Луны составляет 81,3007. Зная их суммарную массу, найденную по параметрам относительной орбиты, можно легко найти и массу каждого из тел.
Говоря об относительном движении, мы можем произвольно выбирать точку отсчета: относительная орбита Земли вокруг Солнца в точности такова, как относительная орбита Солнца вокруг Земли. Проекцию этой орбиты на небесную сферу называют «эклиптикой». В течение года Солнце передвигается по эклиптике приблизительно на 1° в сутки, а если смотреть от Солнца, то так же точно движется Земля. Плоскость эклиптики наклонена к плоскости небесного экватора на 23°27ў, т.е. таков угол между земным экватором и ее орбитальной плоскостью. Все орбиты в Солнечной системе указывают относительно плоскости эклиптики.
Орбиты Луны и планет.
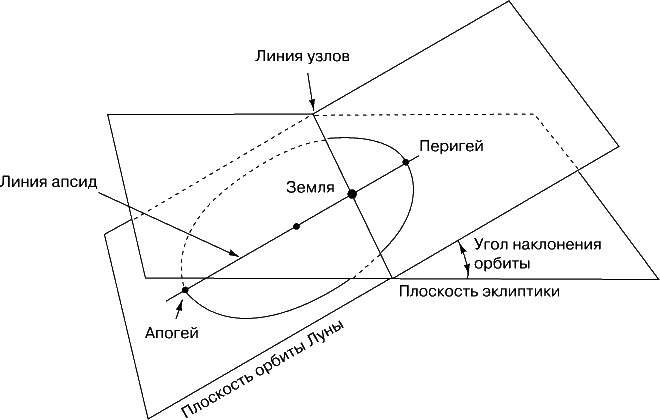
На примере Луны покажем, как описывается орбита (рис. 3). Это относительная орбита, плоскость которой наклонена примерно на 5° к эклиптике. Этот угол называют «наклонением» лунной орбиты. Плоскость лунной орбиты пересекает эклиптику по «линии узлов». Тот из них, где Луна проходит с юга на север, называют «восходящим узлом», а другой – «нисходящим».
Если бы Земля и Луна были изолированы от гравитационного влияния других тел, узлы лунной орбиты всегда имели бы неизменное положение на небе. Но из-за влияния Солнца на движение Луны происходит обратное движение узлов, т.е. они перемещаются по эклиптике на запад, совершая полный оборот за 18,6 лет. Подобно этому, узлы орбит искусственных спутников перемещаются из-за возмущающего влияния экваториального вздутия Земли.
Земля расположена не в центре лунной орбиты, а в одном из ее фокусов. Поэтому в некоторой точке орбиты Луна ближе всего к Земле; это «перигей». В противоположной точке она дальше всего от Земли; это «апогей». (Соответствующие термины для Солнца – «перигелий» и «афелий».) Полусумму расстояний в перигее и апогее называют средним расстоянием; оно равно половине наибольшего диаметра (большой оси) орбиты, поэтому его называют «большой полуосью». Перигей и апогей называют «апсидами», а соединяющую их линию – большую ось – «линией апсид». Если бы не возмущения от Солнца и планет, линия апсид имела бы фиксированное направление в пространстве. Но из-за возмущений линия апсид лунной орбиты движется к востоку с периодом 8,85 лет. То же происходит с линиями апсид искусственных спутников под влиянием экваториального вздутия Земли. У планет линии апсид (между перигелием и афелием) движутся вперед под влиянием других планет. См. также КОНИЧЕСКИЕ СЕЧЕНИЯ.
Размер орбиты определяется длиной большой полуоси, а ее форма – величиной, называемой «эксцентриситетом». Эксцентриситет лунной орбиты вычисляется по формуле:
(Расстояние в апогее – Среднее расстояние) / Среднее расстояние
либо по формуле
(Среднее расстояние – Расстояние в перигее) / Среднее расстояние
Для планет апогей и перигей в этих формулах заменяют на афелий и перигелий. Эксцентриситет круговой орбиты равен нулю; у всех эллиптических орбит он меньше 1,0; у параболической орбиты он в точности равен 1,0; у гиперболических орбит он больше 1,0.
Орбита полностью определена, если указаны ее размер (среднее расстояние), форма (эксцентриситет), наклонение, положение восходящего узла и положение перигея (для Луны) или перигелия (для планет). Эти величины называют «элементами» орбиты. Элементы орбиты искусственного спутника задаются так же, как для Луны, но обычно по отношению не к эклиптике, а к плоскости земного экватора.
Луна обращается вокруг Земли за время, называемое «сидерическим периодом» (27,32 сут); по истечении его она возвращается на исходное место относительно звезд; это ее истинный орбитальный период. Но за это время Солнце перемещается по эклиптике, и Луне требуется еще двое суток, чтобы оказаться в исходной фазе, т.е. в прежнем положении относительно Солнца. Этот промежуток времени называют «синодическим периодом» Луны (ок. 29,5 сут). Так же и планеты обращаются вокруг Солнца за сидерический период, а проходят полный цикл конфигураций – от «вечерней звезды» до «утренней звезды» и обратно – за синодический период. Некоторые элементы орбит планет указаны в таблице. См. также СОЛНЕЧНАЯ СИСТЕМА.
Орбитальная скорость.
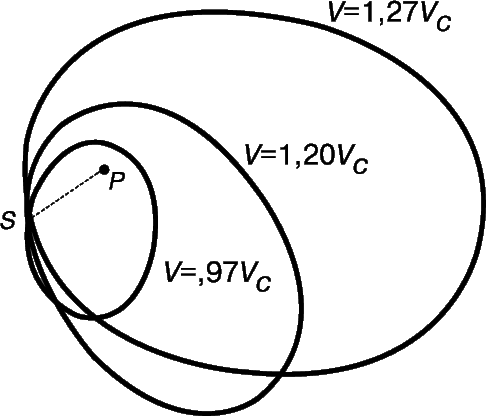
Среднее расстояние спутника от главного компонента определяется его скоростью на некотором фиксированном расстоянии. Например, Земля обращается по почти круговой орбите на расстоянии 1 а.е. (астрономическая единица) от Солнца со скоростью 29,8 км/с; любое другое тело, имеющее на этом же расстоянии такую же скорость, будет также двигаться по орбите со средним расстоянием от Солнца 1 а.е., независимо от формы этой орбиты и направления движения по ней. Таким образом, для тела в заданной точке размер орбиты зависит от значения скорости, а ее форма – от направления скорости (рис. 4).
Это имеет непосредственное отношение к орбитам искусственных спутников. Чтобы вывести спутник на заданную орбиту, необходимо доставить его на определенную высоту над Землей и сообщить ему определенную скорость в определенном направлении. Причем сделать это нужно с высокой точностью. Если требуется, например, чтобы орбита проходила на высоте 320 км и не отклонялась от нее более чем на 30 км, то на высоте 310–330 км его скорость не должна отличаться от расчетной (7,72 км/с) более чем на 5 м/с, а направление скорости должно быть параллельно земной поверхности с точностью 0,08°.
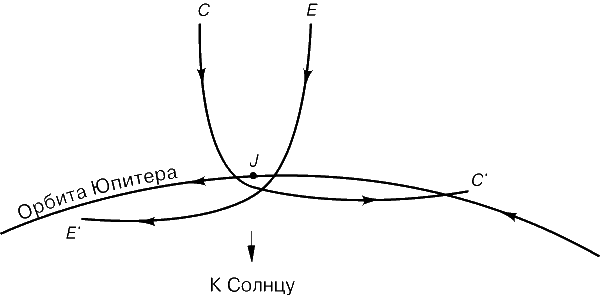
Сказанное выше имеет отношение и к кометам. Обычно они движутся по очень вытянутым орбитам, эксцентриситеты которых нередко достигают 0,99. И хотя их средние расстояния и орбитальные периоды очень велики, в перигелии они могут приближаться к большим планетам, например к Юпитеру. В зависимости от направления, с которого комета подлетает к Юпитеру, он может своим притяжением увеличить или уменьшить ее скорость (рис. 5). Если скорость уменьшится, то комета перейдет на орбиту меньшего размера; в этом случае говорят, что она «захвачена» планетой. Все кометы с периодами менее нескольких миллионов лет, вероятно, были захвачены именно таким образом.
Если же скорость кометы относительно Солнца увеличится, то и орбита ее возрастет. Причем с приближением скорости к определенному пределу рост орбиты стремительно ускоряется. На расстоянии 1 а.е. от Солнца эта предельная скорость равна 42 км/с. С большей скоростью тело движется по гиперболической орбите и никогда уже не возвращается к перигелию. Поэтому данную предельную скорость называют «скоростью убегания» с земной орбиты. Ближе к Солнцу скорость убегания выше, а вдали от Солнца – меньше.
Если комета приближается к Юпитеру с большого расстояния, ее скорость близка к скорости убегания. Поэтому, пролетая вблизи Юпитера, комете достаточно лишь немного увеличить свою скорость, чтобы превысить предел и никогда больше не вернуться в окрестности Солнца. Такие кометы называют «выброшенными».
| ЭЛЕМЕНТЫ ОРБИТ ПЛАНЕТ | ||||||
| Планета | Среднее расстояние от Солнца | Период обращения | Эксцен- триситет |
Наклоне- ние |
||
| млн. км | а.е.* | сидерический | синодический | |||
| Меркурий | 57,9 | 0,38 | 88,0 сут | 116 сут | 0,21 | 7°0 ў |
| Венера | 108,2 | 0,72 | 224,7 сут | 584 сут | 0,01 | 3°24 ў |
| Земля | 149,6 | 1,00 | 365,3 сут | – | 0,02 | – |
| Марс | 227,9 | 1,52 | 687,0 сут | 780 сут | 0,09 | 1°51 ў |
| Юпитер | 778,3 | 5,20 | 11,8 лет | 399 сут | 0,05 | 1°18 ў |
| Сатурн | 1427,0 | 9,53 | 29,5 лет | 378 сут | 0,06 | 2°29 ў |
| Уран | 2869,6 | 19,18 | 84,0 лет | 370 сут | 0,05 | 0°46 ў |
| Нептун | 4496,6 | 30,05 | 164,8 лет | 367 сут | 0,01 | 1°46 ў |
| Плутон | 5900 | 39,44 | 248,4 лет | 367 сут | 0,25 | 17°9 ў |
| * 1 а.е. (астрономическая единица) – среднее расстояние Земли от Солнца. | ||||||
Скорость убегания от Земли.
Понятие о скорости убегания очень важно. Кстати, нередко ее называют также скоростью «ухода» или «ускользания», а еще «параболической» или «второй космической скоростью». Последний термин применяют в космонавтике, когда речь идет о запусках к другим планетам. Как уже было сказано, для движения спутника по низкой круговой орбите ему нужно сообщить скорость около 8 км/с, которую называют «первой космической». (Точнее, если бы не мешала атмосфера, у поверхности Земли она была бы равна 7,9 км/с.) С увеличением скорости спутника у земной поверхности его орбита становится все более вытянутой: ее среднее расстояние возрастает. Когда будет достигнута скорость убегания, аппарат покинет Землю навсегда.
Рассчитать эту критическую скорость довольно просто. Вблизи Земли кинетическая энергия тела должна быть равна работе силы тяжести при перемещении тела с поверхности Земли «на бесконечность». Поскольку притяжение быстро убывает с высотой (обратно пропорционально квадрату расстояния), то можно ограничиться работой на расстоянии радиуса Земли:
Здесь слева кинетическая энергия тела массы m, движущегося со скоростью V, а справа работа силы тяжести mg на расстоянии радиуса Земли (R = 6371 км). Из этого уравнения найдем скорость (причем это не приближенное, а точное ее выражение):
Поскольку ускорение свободного падения у поверхности Земли составляет g = 9,8 м/с2, скорость убегания будет равна 11,2 км/с.
Орбита Солнца.
Само Солнце вместе с окружающими его планетами и малыми телами Солнечной системы движется по своей галактической орбите. По отношению к ближайшим звездам Солнце летит со скоростью 19 км/с в направлении точки в созвездии Геркулеса. Эту точку называют «апексом» солнечного движения. А в целом вся группа ближайших звезд, включая Солнце, обращается вокруг центра Галактики по орбите радиусом 25ґ1016 км со скоростью 220 км/с и периодом 230 млн. лет. Эта орбита имеет довольно сложный вид, поскольку движение Солнца постоянно подвергается возмущению со стороны других звезд и массивных облаков межзвездного газа.
Ответь на вопросы викторины «Физика»