ПЛАНКА ПОСТОЯННАЯ

ПЛАНКА ПОСТОЯННАЯ h, одна из универсальных числовых констант природы, входящая во многие формулы и физические законы, описывающие поведение материи и энергии в масштабах микромира. Существование этой константы было установлено в 1900 профессором физики Берлинского университета М.Планком в работе, заложившей основы квантовой теории. Им же была дана предварительная оценка ее величины. Принятое в настоящее время значение постоянной Планка равно (6,6260755 ± 0,00023)Ч10^–34 ДжЧс.

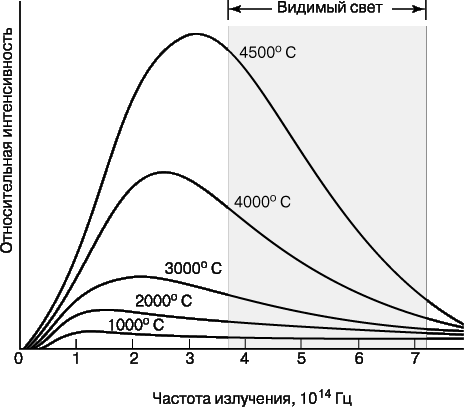
Планк сделал это открытие, пытаясь найти теоретическое объяснение спектра излучения, испускаемого нагретыми телами. Такое излучение испускают все тела, состоящие из большого числа атомов, при любой температуре выше абсолютного нуля, однако оно становится заметным лишь при температурах, близких к температуре кипения воды 100° С и выше нее. Кроме того, оно охватывает весь спектр частот от радиочастотного диапазона до инфракрасной, видимой и ультрафиолетовой областей. В области видимого света излучение становится достаточно ярким лишь примерно при 550° С. Зависимость интенсивности излучения за единицу времени от частоты характеризуется спектральными распределениями, представленными на рис. 1 для нескольких значений температуры. Интенсивность излучения при данном значении частоты есть количество энергии, излучаемой в узкой полосе частот в окрестности данной частоты. Площадь кривой пропорциональна полной энергии, излучаемой на всех частотах. Как нетрудно видеть, эта площадь быстро увеличивается с повышением температуры.

Планк хотел вывести теоретически функцию спектрального распределения и найти объяснение двух простых установленных экспериментально закономерностей: частота, отвечающая наиболее яркому свечению нагретого тела, пропорциональна абсолютной температуре, а полная энергия, излучаемая за 1 с единичной площадкой поверхности абсолютно черного тела, – четвертой степени его абсолютной температуры.

Первую закономерность можно выразить формулой

где nm – частота, соответствующая максимальной интенсивности излучения, Т – абсолютная температура тела, а a – постоянная, зависящая от свойств излучающего объекта. Вторая закономерность выражается формулой

где Е – полная энергия, излучаемая единичной площадкой поверхности за 1 с, s – постоянная, характеризующая излучающий объект, а Т – абсолютная температура тела. Первая формула называется законом смещения Вина, а вторая – законом Стефана – Больцмана. Планк стремился на основании этих законов вывести точное выражение для спектрального распределения излучаемой энергии при любой температуре.

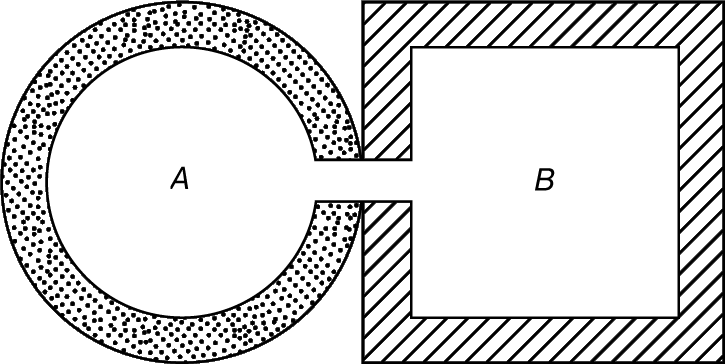
Универсальный характер явления можно было объяснить с позиций второго начала термодинамики, согласно которому тепловые процессы, протекающие самопроизвольно в физической системе, всегда идут в направлении установления в системе теплового равновесия. Представим себе, что два полых тела А и В разной формы, разного размера и из разного материала с одной температурой обращены друг к другу, как показано на рис. 2. Если предположить, что из А в В приходит больше излучения, чем из В в А, то тело В неизбежно становилось бы более теплым за счет А и равновесие самопроизвольно нарушалось бы. Такая возможность исключается вторым началом термодинамики, а следовательно, оба тела должны излучать одинаковое количество энергии, и, стало быть, величина s в формуле (2) не зависит от размера и материала излучающей поверхности, при условии, что последняя представляет собой некую полость. Если полости разделить цветным экраном, который фильтровал бы и отражал обратно все излучение, кроме излучения с какой-либо одной частотой, то все сказанное осталось бы справедливым. Это означает, что количество излучения, испускаемого каждой полостью в каждом участке спектра, одно и то же, и функция спектрального распределения для полости носит характер универсального закона природы, причем величина a в формуле (1), подобно величине s, является универсальной физической константой.

Планк, хорошо владевший термодинамикой, предпочел именно такое решение проблемы и, действуя методом проб и ошибок, нашел термодинамическую формулу, которая позволяла вычислять функцию спектрального распределения. Полученная формула согласовалась со всеми имевшимися экспериментальными данными и, в частности, с эмпирическими формулами (1) и (2). Чтобы объяснить это, Планк воспользовался хитроумной уловкой, подсказанной вторым началом термодинамики. Справедливо полагая, что термодинамика вещества лучше изучена, нежели термодинамика излучения, он сосредоточил свое внимание преимущественно на веществе стенок полости, а не на излучении внутри нее. Поскольку постоянные, входящие в законы Вина и Стефана – Больцмана, не зависят от природы вещества, Планк был вправе делать любые предположения относительно материала стенок. Он выбрал модель, в которой стенки состоят из огромного числа крошечных электрически заряженных осцилляторов, каждый со своей частотой. Осцилляторы под действием падающего на них излучения могут колебаться, излучая при этом энергию. Весь процесс можно было исследовать исходя из хорошо известных законов электродинамики, т.е. функцию спектрального распределения можно было найти, вычислив среднюю энергию осцилляторов с разными частотами. Обратив последовательность рассуждений, Планк, исходя из угаданной им правильной функции спектрального распределения, нашел формулу для средней энергии U осциллятора с частотой n в полости, находящейся в равновесии при абсолютной температуре Т:

где b – величина, определяемая экспериментально, а k – постоянная (называемая постоянной Больцмана, хотя впервые была введена Планком), которая фигурирует в термодинамике и кинетической теории газов. Поскольку эта постоянная обычно входит с множителем Т, удобно ввести новую постоянную h = bk. Тогда b = h/k и формулу (3) можно переписать в виде

Новая постоянная h и представляет собой постоянную Планка; вычисленное Планком ее значение составило 6,55Ч10^–34 ДжЧс, что всего лишь примерно на 1% отличается от современного значения. Теория Планка позволила выразить величину s в формуле (2) через h, k и скорость света с:

Это выражение согласовалось с экспериментом в пределах той точности, с которой были известны константы; позднее более точные измерения не обнаружили расхождений.

Таким образом, проблема объяснения функции спектрального распределения свелась к более «простой» задаче. Нужно было объяснить, каков физический смысл постоянной h или, вернее, произведения hn. Открытие Планка состояло в том, что объяснить ее физический смысл можно, лишь введя в механику совершенно новое понятие «кванта энергии». 14 декабря 1900 на заседании Немецкого физического общества Планк в своем докладе показал, что формулу (4), а тем самым и остальные формулы можно объяснить, если предположить, что осциллятор с частотой n обменивается энергией с электромагнитным полем не непрерывно, а как бы ступенями, приобретая и теряя свою энергию дискретными порциями, квантами, каждый из которых равен hn. См. также ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ; ТЕПЛОТА; ТЕРМОДИНАМИКА. Следствия из сделанного Планком открытия изложены в статьях ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ; КОМПТОНА ЭФФЕКТ; АТОМ; АТОМА СТРОЕНИЕ; КВАНТОВАЯ МЕХАНИКА.

Квантовая механика представляет собой общую теорию явлений в масштабе микромира. Открытие Планка выступает ныне как вытекающее из уравнений этой теории важное следствие особого характера. В частности, оказалось, что оно имеет силу для всех процессов обмена энергией, которые происходят при колебательном движении, например в акустике и в электромагнитных явлениях. Им объясняется высокая проникающая способность рентгеновского излучения, частоты которого в 100–10 000 раз превышают частоты, характерные для видимого света, и кванты которого имеют соответственно более высокую энергию. Открытие Планка служит основой всей волновой теории материи, имеющей дело с волновыми свойствами элементарных частиц и их комбинаций.

Из теории Максвелла известно, что пучок света с энергией Е несет импульс р, равный

где с – скорость света. Если кванты света рассматривать как частицы, каждая из которых имеет энергию hn, то естественно предположить наличие у каждой из них импульса p, равного hn/c. Фундаментальное соотношение, связывающее длину волны l с частотой n и скоростью света с, имеет вид

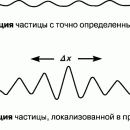
так что выражение для импульса можно записать в виде h/l. В 1923 аспирант Л.де Бройль высказал предположение, что не только свету, но и всем формам материи свойствен корпускулярно-волновой дуализм, выражающийся в соотношениях

между характеристиками волны и частицы. Эта гипотеза подтвердилась, что сделало постоянную Планка универсальной физической константой. Ее роль оказалась гораздо более значительной, чем можно было бы предполагать с самого начала.