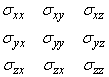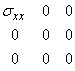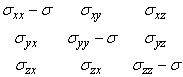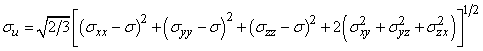ПРОЧНОСТЬ И РАЗРУШЕНИЕ

ПРОЧНОСТЬ И РАЗРУШЕНИЕ. Прочность тела – это его способность сохранять свою целостность под действием внешних факторов, не разделяясь на отдельные фрагменты, в противном случае говорят, что наступило разрушение. Прочность тела не следует путать с его жесткостью: например, если консервная банка сплющилась под колесом автомобиля без разрывов материала, то это означает, что жесткость банки была недостаточной для сохранения формы в этих условиях. Банка как конструкция перестала существовать, но прочность ее материала не была нарушена. Приводят такой наглядный пример: сталь – прочная и жесткая; капрон – прочный, но не жесткий; печенье – жесткое, но непрочное; фруктовое желе – непрочное и нежесткое.

Прочностью обладают, в известной мере, все материалы, все предметы, прочность – необходимое условие их существования, но в то же время при достаточно сильном воздействии все материалы, все тела могут разрушиться. Примеры разрушений хорошо известны: во время землетрясений разрушаются здания, от ветровых нагрузок обрушиваются мосты, разламываются на две части гигантские танкеры, происходят переломы костей конечностей человека, разбивается чашка, ломается карандаш, от радиоактивного облучения рвутся молекулы, в известных условиях раскалываются атомы тяжелых элементов. Известно, что грандиозные средневековые соборы строились столетиями – в значительной мере это связано с тем, что во время постройки обрушивались купола или стены и их приходилось отстраивать заново. Из семи чудес света сохранились только пирамиды – все остальные так или иначе разрушились. Можно сказать, что с процессами прочности и разрушения человек столкнулся в глубокой древности, когда начал осознанно относиться к своей деятельности: нужно было добиться прочности копья, и нужно было добиться правильных сколов камня при изготовлении рубила. Тысячелетиями накапливались знания – опыт передавался потомкам в виде правил, рецептов, где реальные знания были смешаны с магией; были построены храмы, крепости, каналы, огромные статуи – сложные конструкции, вызывающие восхищение; были построены деревянные парусные корабли, прочность которых позволила человечеству открыть и исследовать планету Земля.

Но научный подход к исследованию прочности и разрушения начался с работ двух великих людей – Леонардо да Винчи (1452–1519) и Галилео Галилея (1564–1642). Кажется, что они интересовались всем, что в то время было важным или интересным, и проблема прочности и разрушения не могла не привлечь их внимание.

Леонардо впервые провел спланированные систематические эксперименты, в которых определялись разрушающие нагрузки для балок, струн из органических материалов, проволоки, канатов, для колонн под действием сжимающей нагрузки.

Галилей, по-видимому, ничего не знал об этих исследованиях и начал все сначала. Он установил два фундаментальных результата: при разрыве стержня нагрузка пропорциональна его площади, и при увеличении размеров конструкции и сохранении геометрического подобия «чем больше будет она по размерам, тем менее будет прочна».

Это были очень важные результаты: во-первых, в изучение прочности были введены мера и число. Теперь каждому материалу можно было сопоставить предел прочности (s*), т.е. напряжение, при котором разрушается при растяжении стержень из этого материала. Во-вторых, было установлено, что в случаях, более сложных, чем растяжение (например, изгиб), разрушающая нагрузка уже не пропорциональна площади и ее определение есть сложная проблема; подходы к решению этой проблемы привели к созданию фундаментальной теории упругости и прикладной теории сопротивления материалов действию нагрузок. Оказалось, что в теле, находящемся под действием внешних сил, возникает система внутренних сил, напряжений, которые математически в каждой точке тела описываются с помощью тензора напряжений. В фиксированной системе координат XYZ этот тензор записывается в виде матрицы.

В случае растяжения стержня, ось которого совпадает с осью, эта матрица одна и та же во всех точках и имеет только одну ненулевую компоненту:

и поэтому условие прочности имеет очевидную простую форму

s_xx =s*

Но как должно выглядеть условие прочности, когда многие компоненты тензора отличны от нуля, установить не так просто. Были предложены различные гипотезы, которые называются «критериями прочности» для металлов. Как оказалось, наиболее соответствовал опытным данным критерий «энергии формоизменения». В упругом теле напряженное состояние в малой окрестности точки, точнее говоря, тензор напряжений, можно разделить на две части, причем одна часть отвечает только за изменение объема, а другая – за изменение формы при неизменном объеме. Это последнее математически описывается девиатором напряжений, матрица которого получается следующим образом: из диагональных элементов матрицы вычитается их среднее арифметическое s,

s = 1/3(s_xx + s_yy + s_zz)

В результате получается матрица

Напряженному состоянию, которое описывается этой матрицей соответствует упругая энергия формоизменения, пропорциональная выражению

(s_xx– s)\up122 + (s_yy – s)\up122 + (s_zz – s)\up122 + 2(s_{yx\up12 2} + s_{yz\up12 2} + s_{xz\up12 2})

Квадратный корень из этого выражения называют интенсивностью напряжений s_u,

коэффициент выбран так, чтобы при простом растяжении получалось

s_u =s_x

Критерий прочности, который мы обсуждаем, записывается, таким образом, в виде условия

s_u =s*

Оно означает, что разрушение материала начинается в той точке, где напряженное состояние таково, что выражение для s_u впервые достигает значения предела прочности s*.

Этот критерий во многих случаях позволяет обеспечить прочность конструкции путем введения коэффициента запаса прочности n, который обычно выбирают в пределах от 1,1 до 5, в зависимости от надежности расчетов, качества материала и ответственности конструкции. В этом случае критерий прочности записывают в следующем виде:

s_u =s*/ n

Но оказалось, что обеспечить прочность конструкции с помощью критерия прочности можно не всегда. Ответственные конструкции, рассчитанные с учетом всех требований теории прочности, в некоторых случаях разрушались. Гибли самолеты, разламывались и тонули корабли, обрушивались мосты, поезда сходили с рельсов. И исследование прочности и разрушения продолжалось. Было выяснено, что любой кристалл, решетка которого не содержит неправильностей – дефектов – имел бы прочность, в сотни раз превышающую прочность реально существующих аналогичных кристаллов. И главной причиной снижения прочности являются трещины, которые всегда присутствуют в реальных телах, хотя могут иметь микроскопические размеры. И если под влиянием нагрузок, действующих на тело, одна из трещин попадает в условия, при которых она начинает расти, и если рост трещины будет продолжаться, то наступает разрушение. Начало теории роста трещин положили работы Гриффитса (Griffith A.A.), а затем эта теория развилась в механику разрушения, которая существенно дополнила классическую науку о прочности. Механика разрушения изучает прочность тела, учитывая начальное распределение трещин в теле и закономерности роста и развития трещин. Конечно, возникающие при этом задачи очень сложны и многие из них не поддаются решению в настоящее время. Но конкретные расчеты по правилам механики разрушения не многим сложнее обычного расчета на прочность. Познакомиться с идеями и методами механики разрушения можно по книгам, указанным в библиографическом списке.

С развитием и ростом микротрещины связано еще одно явление – усталость материалов. Усталостное разрушение происходит в деталях, подвергающихся переменным, циклическим нагрузкам, когда величина нагрузки в каждом цикле очень мала, но число циклов достигает миллионов и десятков миллионов. В таких условиях работают рельсы, оси вагонов, лонжероны лопастей винта вертолета и многие другие детали конструкций.

Владимир Кузнецов