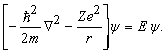СПЕКТРОСКОПИЯ
СПЕКТРОСКОПИЯ, раздел физики, посвященный изучению спектров электромагнитного излучения. Здесь мы рассмотрим оптическую спектроскопию часто называют просто спектроскопией.
Свет – это электромагнитное излучение с длиной волны l от 10–3 до 10–8 м. Этот диапазон длин волн включает инфракрасную (ИК), видимую и ультрафиолетовую (УФ) области. Инфракрасный интервал спектра (l = 1 мм ё 750 нм) подразделяется на дальнюю (1 мм ё 50 мкм), среднюю (50 ё 2,5 мкм) и ближнюю (2,5 мкм ё 750 нм) области. При комнатной температуре любое материальное тело излучает в дальней инфракрасной области, при температуре белого каления излучение сдвигается в ближнюю инфракрасную, а затем и в видимую часть спектра. Видимый спектр простирается от 750 нм (красная граница) до 400 нм (фиолетовая граница). Свет этих длин волн воспринимается человеческим глазом, и именно на эту область приходится большое число спектральных линий атомов. Диапазон от 400 до 200 нм соответствует ультрафиолетовой области, далее примерно до 1 ё 10 нм следует вакуумный ультрафиолет. См. также ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ; СПЕКТР.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
Каждый атом и молекула имеют уникальное строение, которому соответствует свой уникальный спектр.
Структура спектра атома, молекулы или образованной ими макросистемы определяется их энергетическими уровнями. Согласно законам квантовой механики, каждый энергетический уровень соответствует определенному квантовому состоянию. Электроны и ядра в таком состоянии совершают характерные периодические движения, для которых энергия, орбитальный момент количества движения и другие физические величины строго определены и квантованы, т.е. принимают лишь разрешенные дискретные значения, соответствующие целым и полуцелым значениям квантовых чисел. Если известны силы, связывающие электроны и ядра в единую систему, то по законам квантовой механики можно рассчитать ее уровни энергии и квантовые числа, а также предсказать интенсивности и частоты спектральных линий. С другой стороны, анализируя спектр конкретной системы, можно определить энергии и квантовые числа состояний, а также сделать выводы относительно действующих в ней сил. Таким образом, спектроскопия является основным источником сведений о квантово-механических величинах и о строении атомов и молекул. См. также КВАНТОВАЯ МЕХАНИКА.
В атоме наиболее сильное взаимодействие между ядром и электронами обусловлено электростатическими, или кулоновскими силами. Каждый электрон притягивается к ядру и отталкивается всеми остальными электронами (см. также АТОМА СТРОЕНИЕ). Это взаимодействие определяет структуру энергетических уровней электронов. Внешние (валентные) электроны, переходя с уровня на уровень, испускают или поглощают излучение в ближней инфракрасной, видимой и ультрафиолетовой областях. Энергии переходов между уровнями внутренних оболочек соответствуют вакуумной ультрафиолетовой и рентгеновской областям спектра. Более слабым является воздействие электрического поля на магнитные моменты электронов. Это приводит к расщеплению электронных уровней энергии и, соответственно, каждой спектральной линии на компоненты (тонкая структура). Кроме того, ядро, обладающее ядерным моментом, может взаимодействовать с электрическим полем орбитальных электронов, вызывая дополнительное сверхтонкое расщепление уровней энергии.
При сближении двух или более атомов между их электронами и ядрами начинают действовать силы взаимного притяжения и отталкивания. Итоговый баланс сил может привести к уменьшению полной энергии системы атомов – в этом случае образуется стабильная молекула. Строение молекулы в основном определяется валентными электронами атомов, а молекулярные связи подчиняются законам квантовой механики. В молекуле наиболее часто встречаются ионные и ковалентные связи (см. также ХИМИЯ; МОЛЕКУЛ СТРОЕНИЕ). Атомы в молекуле испытывают непрерывные колебания, а сама молекула вращается как целое, поэтому у нее возникают новые энергетические уровни, отсутствующие в изолированных атомах. Энергии вращения меньше колебательных энергий, а колебательные – меньше электронных. Таким образом, в молекуле каждый электронный уровень энергии расщепляется на ряд близко расположенных колебательных уровней, а каждый колебательный уровень, в свою очередь, на тесно расположенные вращательные подуровни. В результате в молекулярных спектрах колебательные переходы имеют вращательную структуру, а электронные – колебательную и вращательную. Переходы между вращательными уровнями одного и того же колебательного состояния попадают в дальнюю инфракрасную и микроволновую области, а переходы между колебательными уровнями одного и того же электронного состояния соответствуют по частотам инфракрасной области. Благодаря расщеплению колебательных уровней на вращательные подуровни каждый переход распадается на множество колебательно-вращательных переходов, образуя полосы. Аналогично электронные спектры молекул представляют собой ряд электронных переходов, расщепленных тесно расположенными подуровнями колебательных и вращательных переходов.
Поскольку каждый атом является квантовой системой (т.е. подчиняется законам квантовой механики), его свойства, в том числе частоты и интенсивности спектральных линий, могут быть рассчитаны, если для данной конкретной системы задан ее гамильтониан. Гамильтониан Н – это полная энергия атома (кинетическая плюс потенциальная), представленная в операторной форме. (Квантово-механический оператор – математическое выражение, с помощью которого вычисляются физические величины.) Кинетическая энергия частицы с массой т и моментом р равна р2/2m. Потенциальная энергия системы равна сумме энергий всех взаимодействий, связывающих систему в единое целое. Если гамильтониан задан, то энергию Е каждого квантового состояния можно найти, решив уравнение Шрёдингера Нy = Еy, где y – волновая функция, описывающая квантовое состояние системы.
СПЕКТРЫ И СТРУКТУРА АТОМОВ
Атом водорода.
С точки зрения квантовой механики атом водорода и любой водородоподобный ион (например, He++ и др.) представляют собой простейшую систему, состоящую из одного электрона с массой m и зарядом -e, который движется в кулоновском поле ядра, имеющего массу М и заряд +Ze (Z – порядковый номер элемента). Если учитывать только электростатическое взаимодействие, то потенциальная энергия атома равна -Ze2/r, и гамильтониан будет иметь вид H = p2/2m -Ze2/r, где m = тМ/(m + M) @ m. В дифференциальной форме оператор p2 равен - ћ 2С2, где ћ = h /2p. Таким образом, уравнение Шрёдингера принимает вид
Решение этого уравнения определяет энергии стационарных состояний (Е < 0) водоподобного атома:
Так как m/M @ 1/2000 и m близко к m, то
En = –RZ2/n2.
где R – постоянная Ридберга, равная R = me4/2ћ2 @ 13,6 эВ (или @ 109678 см-1); в рентгеновской спектроскопии ридберг часто используется в качестве единицы энергии. Квантовые состояния атома определяются квантовыми числами n, l и ml . Главное квантовое число п принимает целые значения 1, 2, 3.... Азимутальное квантовое число l определяет величину момента количества движения электрона относительно ядра (орбитальный момент); при данном п оно может принимать значения l = 0, 1, 2,..., п - 1. Квадрат орбитального момента равен l(l + l) ћ2. Квантовое число ml определяет величину проекции орбитального момента на заданное направление, оно может принимать значения ml = 0, ±1, ±2,..., ± l. Сама проекция орбитального момента равна ml ћ. Значения l = 0, 1, 2, 3, 4, ... принято обозначать буквами s, p, d, f, g,.... Следовательно, уровень 2рводорода имеет квантовые числа п = 2и l = 1.
Вообще говоря, спектральные переходы могут происходить отнюдь не между всеми парами уровней энергии. Электрические дипольные переходы, сопровождающиеся наиболее сильными спектральными проявлениями, имеют место лишь при выполнении определенных условий (правил отбора). Переходы, которые удовлетворяют правилам отбора, называются разрешенными, вероятность остальных переходов значительно меньше, они трудны для наблюдения и считаются запрещенными.
В атоме водорода переходы между состояниями пlmlи пўlўmlў возможны в том случае, если число l изменяется на единицу, а число ml остается постоянным или изменяется на единицу. Таким образом, правила отбора можно записать:
Dl = l – lў = ±1, Dml = mlў = 0, ±1.
Для чисел п и пў правил отбора не существует.
При квантовом переходе между двумя уровнями с энергиями Enў и Enатом испускает или поглощает фотон, энергия которого равна DЕ = Enў - En. Поскольку частота фотона n = DЕ/h, частоты спектральных линий атома водорода (Z = 1) определяются формулой
а соответствующая длина волны равна l = с/n. При значениях пў = 2, п = 3, 4, 5,... частоты линий в эмиссионном спектре водорода соответствуют серии Бальмера (видимый свет и ближняя ультрафиолетовая область) и хорошо согласуются с эмпирической формулой Бальмера ln = 364,56 n2/(n2- 4) нм. Из сравнения этих двух выражений можно определить значение R. Спектроскопические исследования атомарного водорода – прекрасный пример теории и эксперимента, внесших огромный вклад в фундаментальную науку.
Тонкая структура атома водорода.
Рассмотренная выше релятивистская квантовомеханическая теория уровней в основном подтверждалась анализом атомных спектров, однако не объясняла расщепление и тонкую структуру энергетических уровней атома водорода. Объяснить тонкую структуру уровней атомарного водорода позволил учет двух специфических релятивистских эффектов: спин-орбитального взаимодействия и зависимости массы электрона от скорости. Концепция спина электрона, первоначально возникшая из анализа экспериментальных данных, получила теоретическое обоснование в разработанной П.Дираком релятивистской теории, из которой следовало, что электрон обладает собственным моментом количества движения, или спином, ![]() и соответствующим магнитным моментом
и соответствующим магнитным моментом ![]() . Спиновое квантовое число s равно 1/2, а проекция спина на фиксированную ось принимает значения ms = ±1/2. Электрон, двигаясь по орбите в радиальном электрическом поле ядра, создает магнитное поле. Взаимодействие собственного магнитного момента электрона с этим полем называется спин-орбитальным взаимодействием.
. Спиновое квантовое число s равно 1/2, а проекция спина на фиксированную ось принимает значения ms = ±1/2. Электрон, двигаясь по орбите в радиальном электрическом поле ядра, создает магнитное поле. Взаимодействие собственного магнитного момента электрона с этим полем называется спин-орбитальным взаимодействием.
Дополнительный вклад в тонкую структуру дает релятивистская поправка к кинетической энергии, возникающая благодаря высокой орбитальной скорости электрона. Этот эффект был впервые обнаружен Н.Бором и А.Зоммерфельдом, которые показали, что релятивистское изменение массы электрона должно вызывать прецессию его орбиты.
Учет спин-орбитального взаимодействия и релятивистской поправки к массе электрона дает следующее выражение для энергии тонкого расщепления уровней:
где a = e2/ћc »1/137. Полный угловой момент электрона ![]() равен
равен ![]() + s. Для данного значения l квантовое число j принимает положительные значения j = l ± s (j = 1/2 для l = 0). Согласно спектроскопической номенклатуре состояние с квантовыми числами n, l, s, j обозначается как n2s + llj. Это значит, что 2p уровень водорода с n = 2 и j = 3/2 запишется в виде 22p3/2. Величина 2s + 1 называется мультиплетностью; она показывает число состояний, связанных с данным значением s. Заметим, что энергия расщепления уровня при данном n зависит только от j, но не от l или s в отдельности. Таким образом, согласно вышеприведенной формуле 22s1/2 и 22p1/2 уровни тонкой структуры вырождены по энергии. Подобным образом вырождены и уровни 32p3/2 и 32d3/2. Эти результаты согласуются с выводами теории Дирака, если пренебречь членами aZ более высокого порядка. Разрешенные переходы определяются правилами отбора по j: Dj = 0, ±1 (исключая j = 0 ® 0).
+ s. Для данного значения l квантовое число j принимает положительные значения j = l ± s (j = 1/2 для l = 0). Согласно спектроскопической номенклатуре состояние с квантовыми числами n, l, s, j обозначается как n2s + llj. Это значит, что 2p уровень водорода с n = 2 и j = 3/2 запишется в виде 22p3/2. Величина 2s + 1 называется мультиплетностью; она показывает число состояний, связанных с данным значением s. Заметим, что энергия расщепления уровня при данном n зависит только от j, но не от l или s в отдельности. Таким образом, согласно вышеприведенной формуле 22s1/2 и 22p1/2 уровни тонкой структуры вырождены по энергии. Подобным образом вырождены и уровни 32p3/2 и 32d3/2. Эти результаты согласуются с выводами теории Дирака, если пренебречь членами aZ более высокого порядка. Разрешенные переходы определяются правилами отбора по j: Dj = 0, ±1 (исключая j = 0 ® 0).
Спектры щелочных металлов.
В атомах щелочных металлов Li, Na, K, Rb, Cs и Fr на внешней орбите находится один валентный электрон, ответственный за образование спектра. Все остальные электроны расположены на внутренних замкнутых оболочках. В отличие от водородного атома, у атомов щелочных металлов поле, в котором движется внешний электрон, не является полем точечного заряда: внутренние электроны экранируют ядро. Степень экранирования зависит от характера орбитального движения внешнего электрона и его расстояния от ядра. Экранирование наиболее эффективно при больших значениях l и наименее эффективно для s-состояний, где электрон находится ближе всего к ядру. При больших n и l система энергетических уровней подобна водородной.
Тонкая структура уровней у атомов щелочных металлов также подобна водородной. Каждое электронное состояние расщепляется на две близкие компоненты. Разрешенные переходы в обоих случаях определяются одинаковыми правилами отбора. Поэтому спектры атомов щелочных металлов подобны спектру атомарного водорода. Однако у щелочных металлов расщепление спектральных линий при малых п больше, чем у водорода, и быстро растет с увеличением Z.
Многоэлектронные атомы.
Для атомов, содержащих более одного валентного электрона, уравнение Шрёдингера может быть решено лишь приближенно. В приближении центрального поля предполагается, что каждый электрон движется в центрально-симметричном поле, создаваемом ядром и другими электронами. В этом случае состояние электрона полностью определяется квантовыми числами п, l, ml и ms (ms – проекция спина на фиксированную ось). Электроны в многоэлектронном атоме образуют оболочки, энергии которых растут по мере увеличения квантового числа п. Оболочки с n = 1, 2, 3... обозначаются буквами K, L, M ... и т.д. Согласно принципу Паули, в каждом квантовом состоянии не может находиться более одного электрона, т.е. никакие два электрона не могут иметь одинаковый набор квантовых чисел п, l, ml и ms.Это приводит к тому, что оболочки в многоэлектронном атоме заполняются в строго определенном порядке и каждой оболочке соответствует строго определенное число электронов. Электрон с квантовыми числами п и l обозначается сочетанием пs, если l = 0, сочетанием пр, если l = 1, и т. д. Электроны последовательно заполняют оболочки с наименьшей возможной энергией. В первую очередь двумя 1s электронами заполняется K-оболочка, имеющая минимальную энергию; ее конфигурация обозначается 1s2. Следующей заполняется L-оболочка: сначала двумя 2s электронами, затем шестью 2р электронами (конфигурация замкнутой оболочки 2s22р6). По мере роста порядкового номера элемента заполняются все более далекие от ядра оболочки. Заполненные оболочки имеют сферически симметричное распределение заряда, нулевой орбитальный момент и прочно связанные электроны. Внешние, или валентные, электроны связаны гораздо слабее; они определяют физические, химические и спектральные свойства атома. Структура периодической системы элементов хорошо объясняется порядком заполнения оболочек атомов, находящихся в основных состояниях. См. также ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ.
В приближении центрального поля принимается, что все квантовые состояния, принадлежащие данной конфигурации, имеют одинаковую энергию. В действительности эти состояния расщепляются двумя основными возмущениями: спин-орбитальным и остаточным кулоновским взаимодействиями. Эти взаимодействия по-разному связывают спиновые и орбитальные моменты отдельных электронов внешней оболочки. В том случае, когда преобладает остаточное кулоновское взаимодействие, имеет место LS тип связи, а если преобладает спин-орбитальное взаимодействие, то осуществляется jj тип связи.
В случае LS-связи орбитальные моменты внешних электронов образуют полный орбитальный момент![]() , а спиновые моменты – полный спиновый момент
, а спиновые моменты – полный спиновый момент ![]() . Сложение
. Сложение![]() и
и ![]() дает полный момент
дает полный момент ![]() атома. В случае jj-связи орбитальный
атома. В случае jj-связи орбитальный ![]() и спиновый
и спиновый ![]() моменты электрона с номером i, складываясь, образуют полный момент электрона
моменты электрона с номером i, складываясь, образуют полный момент электрона ![]() , а при сложении всех векторов
, а при сложении всех векторов ![]() получается полный угловой момент атома
получается полный угловой момент атома ![]() . Общее число квантовых состояний для обоих типов связи, естественно, одно и то же.
. Общее число квантовых состояний для обоих типов связи, естественно, одно и то же.
В многоэлектронных атомах правила отбора для разрешенных переходов зависят от типа связи. Помимо этого, существует правило отбора по четности: в разрешенных электрических дипольных переходах четность квантового состояния должна изменяться. (Четность – это квантовое число, означающее четность (+1) или нечетность (–1) волновой функции при отражении от начала координат.) Правило отбора по четности является основным требованием для электрического дипольного перехода в атоме или молекуле.
Сверхтонкая структура.
Такие характеристики атомных ядер, как масса, объем, магнитный и квадрупольный моменты, влияют на структуру электронных уровней энергии, вызывая их расщепление на очень тесно расположенные подуровни, называемые сверхтонкой структурой.
Взаимодействия, вызывающие сверхтонкое расщепление электронных уровней, которые зависят от электронно-ядерной ориентации, могут быть магнитными или электрическими. В атомах преобладают магнитные взаимодействия. В этом случае сверхтонкая структура возникает в результате взаимодействия ядерного магнитного момента с магнитным полем, которое создается в области ядра спинами и орбитальным движением электронов. Энергия взаимодействия зависит от полного углового момента системы![]() , где
, где ![]() – ядерный спин, а I – соответствующее ему квантовое число. Сверхтонкое магнитное расщепление уровней энергии определяется формулой
– ядерный спин, а I – соответствующее ему квантовое число. Сверхтонкое магнитное расщепление уровней энергии определяется формулой
где А – постоянная сверхтонкой структуры, пропорциональная магнитному моменту ядра. В спектре обычно наблюдаются частоты от сотен мегагерц до гигагерц. Они максимальны для s-электронов, орбиты которых наиболее близки к ядру.
Распределение заряда в ядре, степень асимметрии которого характеризуется квадрупольным моментом ядра, также влияет на расщепление энергетических уровней. Взаимодействие квадрупольного момента с электрическим полем в области ядра очень мало, а частоты вызванного им расщепления составляют несколько десятков мегагерц.
Сверхтонкая структура спектров может быть обусловлена так называемым изотопическим смещением. Если элемент содержит несколько изотопов, то в его спектре наблюдаются слабо разделенные или перекрывающиеся линии. В этом случае спектр представляет собой совокупность слегка смещенных друг относительно друга наборов спектральных линий, принадлежащих разным изотопам. Интенсивность линий каждого изотопа пропорциональна его концентрации.
СТРУКТУРА И СПЕКТРЫ МОЛЕКУЛ
Молекулярные спектры гораздо сложнее и разнообразнее атомных. Это обусловлено тем, что в молекулах имеются дополнительные степени свободы и наряду с движением электронов вокруг ядер атомов, образующих молекулу, происходят колебания самих ядер относительно равновесного положения, а также вращение молекулы как целого. Ядра в молекуле образуют линейную, плоскую или трехмерную конфигурацию. Плоская и трехмерная молекулы, состоящие из N атомов, обладают 3N–6 колебательными и тремя вращательными степенями свободы, а линейная – 3N–5 колебательными и двумя вращательными степенями свободы. Таким образом, молекула кроме электронной энергии имеет колебательную и вращательную внутренние энергии, а также новые системы уровней.
Вращательные спектры.
Двухатомную молекулу можно упрощенно рассматривать как жесткий ротатор с моментом инерции I. Решение уравнения Шрёдингера для жесткого ротатора дает следующие разрешенные уровни энергии:
где J – квантовое число, характеризующее вращательный момент количества движения молекулы. Правило отбора для разрешенных переходов таково: DJ = ±1. Следовательно, чисто вращательный спектр состоит из ряда эквидистантных линий с частотами
Вращательные спектры многоатомных молекул имеют сходную структуру.
Колебательно-вращательные спектры.
В действительности молекулярные связи не являются жесткими. В простейшем приближении движение ядер двухатомной молекулы можно рассматривать как колебания частиц с приведенной массой m относительно положения равновесия в потенциальной яме с гармоническим потенциалом. Если гармонический потенциал имеет вид V(x) = kx2/2, где x – отклонение межъядерного расстояния от равновесного, а k – коэффициент упругости, то решение уравнение Шрёдингера дает следующие возможные уровни энергии: Еv = hn (v+1/2). Здесь n – частота колебаний, определяемая формулой ![]() , а v – колебательное квантовое число, принимающее значения v = 1, 2, 3.... Правило отбора для разрешенных (инфракрасных) переходов: Dv = ±1. Таким образом, для колебательных переходов существует единственная частота n. Но поскольку в молекуле одновременно происходят колебания и вращение, возникает колебательно-вращательный спектр, в котором на колебательную частоту молекулы налагается «гребенка» вращательных линий.
, а v – колебательное квантовое число, принимающее значения v = 1, 2, 3.... Правило отбора для разрешенных (инфракрасных) переходов: Dv = ±1. Таким образом, для колебательных переходов существует единственная частота n. Но поскольку в молекуле одновременно происходят колебания и вращение, возникает колебательно-вращательный спектр, в котором на колебательную частоту молекулы налагается «гребенка» вращательных линий.
Электронные спектры.
У молекул имеется большое число возбужденных электронных уровней, переходы между которыми сопровождаются изменением колебательной и вращательной энергии. В результате этого структура электронных спектров молекул существенно усложняется, поскольку: 1) электронные переходы часто перекрываются; 2) не соблюдается правило отбора для колебательных переходов (отсутствует ограничение по Dv); 3) сохраняется правило отбора DJ = 0, ±1 для разрешенных вращательных переходов. Электронный спектр представляет собой серию колебательных полос, каждая из которых содержит десятки или сотни вращательных линий. Как правило, в молекулярных спектрах наблюдаются несколько электронных переходов в близкой инфракрасной, видимой и ультрафиолетовой областях. Например, в спектре молекулы иода (J2) имеется около 30 электронных переходов.
С появлением лазеров исследование электронных спектров молекул, особенно многоатомных, вышло на новый уровень. Перестраиваемое в широких пределах интенсивное лазерное излучение используется в спектроскопии высокого разрешения для точного определения молекулярных констант и потенциальных поверхностей. Лазеры с видимым, инфракрасным и микроволновым излучением применяются в экспериментах по двойному резонансу для исследования новых переходов. См. также МОЛЕКУЛ СТРОЕНИЕ.
Инфракрасные спектры и спектры комбинационного рассеяния.
Молекулярные спектры поглощения обусловлены электрическими дипольными переходами. Электрический диполь – это совокупность двух точечных электрических зарядов, равных по величине, противоположных по знаку и находящихся на некотором расстоянии друг от друга. Произведение положительного заряда на расстояние между зарядами называется электрическим дипольным моментом. Чем больше дипольный момент, тем сильнее система может поглощать и излучать электромагнитную энергию. У полярных молекул, таких, как HBr, имеющих большой дипольный момент и сильно поглощающих на соответствующих частотах, наблюдаются колебательно-вращательные спектры. С другой стороны, неполярные молекулы, такие, как Н2, О2 и N2, не имеют постоянного дипольного момента, и, следовательно, не могут при вращении излучать или поглощать электромагнитную энергию, поэтому у них отсутствуют вращательные спектры. К тому же колебания таких молекул столь симметричны, что не приводят к появлению дипольного момента. Этим обусловлено отсутствие у них инфракрасного колебательного спектра.
Важным спектроскопическим методом исследования структуры молекул является изучение рассеяния света. Рассеяние света – это процесс, в котором под действием падающего света в атоме или молекуле возбуждаются колебания дипольного момента, сопровождающиеся излучением полученной энергии. Переизлучение происходит в основном на частоте падающего света (упругое рассеяние), но может наблюдаться слабое неупругое рассеяние на смещенных (комбинационных) частотах. Упругое рассеяние называется рэлеевским, а неупругое – рамановским или комбинационным. Линии, соответствующие комбинационному рассеянию, смещены относительно линии падающего света на частоту молекулярных колебаний рассеивающего образца. Поскольку молекула может еще и вращаться, на частоту смещения налагаются вращательные частоты.
Молекулы с гомеополярной связью, не имеющие инфракрасного спектра, следует изучать методом комбинационного рассеяния. В случае многоатомных молекул с несколькими частотами колебаний часть спектральной информации можно получить из инфракрасных спектров поглощения, а часть – из спектров комбинационного рассеяния (в зависимости от симметрии колебаний). Полученные сведения дополняют друг друга, поскольку благодаря разным правилам отбора содержат информацию о разных молекулярных колебаниях.
Инфракрасная и рамановская спектроскопия многоатомных молекул является мощным аналитическим методом, подобным спектрохимическому анализу атомов. Каждой молекулярной связи соответствует характерная колебательная закономерность в спектре, по которой можно идентифицировать молекулу или определить ее структуру.
Эффекты Зеемана и Штарка.
Внешние электрическое и магнитное поля успешно применяются для изучения природы и свойств энергетических уровней.
В 1896 П.Зееман обнаружил, что в спектре образца, помещенного во внешнее магнитное поле, каждая спектральная линия расщепляется на ряд компонент. Аналогичный эффект, но во внешнем электрическом поле, наблюдал И.Штарк в 1913. Для изучения атомов удобнее применять магнитное поле, а для исследования молекул больше подходит электрическое поле. См. также ШТАРКА ЭФФЕКТ; ЗЕЕМАНА ЭФФЕКТ.
УШИРЕНИЕ СПЕКТРАЛЬНОЙ ЛИНИИ
В соответствии с законами квантовой механики спектральные линии всегда имеют конечную ширину, характерную для данного атомного или молекулярного перехода. Важной характеристикой квантового состояния является его радиационное время жизни t, т.е. время, в течение которого система остается в этом состоянии, не переходя на более низкие уровни. С точки зрения классической механики излучение представляет собой цуг волн длительностью t, откуда следует, что ширина линии излучения Dn равна 1/2pt. Чем меньше время жизни t, тем шире линия.
Радиационное время жизни зависит от дипольного момента перехода и частоты излучения. Самые большие моменты перехода соответствуют электрическим дипольным переходам. В атомах и молекулах для сильных электронных переходов в видимой области спектра t » 10 нс, чему соответствует ширина линии от 10 до 20 МГц. Для возбужденных колебательных состояний, излучающих в инфракрасном диапазоне, моменты переходов слабее, а длина волны больше, поэтому их радиационные времена жизни измеряются миллисекундами.
Радиационное время жизни определяет минимальную ширину спектральной линии. Однако в подавляющем большинстве случаев спектральные линии могут быть намного шире. Причины этого –хаотическое тепловое движение (в газе), столкновения между излучающими частицами, сильные возмущения частоты ионов, обусловленные их случайным расположением в кристаллической решетке. Существует ряд методов минимализации ширины линий, позволяющих измерять центральные частоты с максимально возможной точностью.
СПЕКТРАЛЬНЫЕ ПРИБОРЫ
Простейшим оптическим прибором, предназначенным для разложения света на спектральные составляющие и визуального наблюдения спектра, является спектроскоп. Современные спектроскопы, снабженные устройствами для измерения длин волн, называются спектрометрами. Квантометры, полихроматоры, квантоваки и др. также относятся к семейству спектрографов. В спектрографах спектр регистрируется одновременно в широком диапазоне длин волн; для записи спектров используются фотопластинки и многоканальные детекторы (фотодиодные линейки, фотодиодные матрицы). В спектрофотометрах осуществляется фотометрирование, т.е. сравнение измеряемого потока излучения с эталонным, и производится электронная запись спектров. Эмиссионный спектрометр обычно состоит из источника излучения (излучаемый образец), щелевой диафрагмы, коллимирующей линзы или коллимирующего зеркала, диспергирующего элемента, фокусирующей системы (линзы или зеркала) и детектора. Щель вырезает узкий пучок света от источника, коллимирующая линза расширяет его и преобразует его в параллельный. Диспергирующий элемент разлагает свет на спектральные составляющие. Фокусирующая линза создает изображение щели в фокальной плоскости, где помещается детектор. При изучении поглощения применяется источник со сплошным спектром, а ячейка с поглощающим образцом помещается в определенных точках на пути светового потока.
Источники.
Источниками непрерывного ИК-излучения служат нагретые до высоких температур стержни из карбида кремния (глобары), обладающие интенсивным излучением с l > 3 мкм. Для получения непрерывного спектра в видимой, ближней ИК- и ближней УФ-областях лучшими общепринятыми источниками считаются твердые тела каления. В вакуумной УФ-области используются водородные и гелиевые разрядные лампы. Электрические дуги, искры и разрядные трубки – традиционные источники линейчатых спектров нейтральных и ионизованных атомов.
Превосходными источниками являются лазеры, генерирующие интенсивное монохроматическое коллиминированное когерентное излучение во всем оптическом диапазоне. Среди них особого внимания заслуживают источники с широким диапазоном перестройки частоты. Так, например, диодные ИК-лазеры можно перестраивать в интервале от 3 до 30 мкм, лазеры на красителях – в пределах видимой и ближней ИК областей. Преобразование частоты расширяет область перестройки последних от средней ИК- до дальней УФ-области. Имеется большое число лазерных источников, перестраиваемых в более узких диапазонах, и многочисленное семейство лазеров с фиксированной частотой, позволяющих перекрыть всю область спектра от дальней ИК- до УФ-области. Лазерные источники вакуумного УФ-излучения с преобразованием частоты генерируют излучение с длиной волны всего лишь в несколько нанометров. Разработаны также лазеры с фиксированной частотой, работающие в рентгеновском диапазоне.
Методы спектрального разложения.
Спектральное разложение света осуществляется тремя методами: дисперсией за счет преломления в призмах, дифракцией на периодических решетках и с использованием интерференции. Призмы для ИК-области изготавливаются из различных неорганических кристаллов, для видимого и УФ-излучения – из стекла и кварца соответственно. В большинстве современных приборов вместо призм применяются дифракционные решетки с большим числом тесно расположенных штрихов. Спектрометры с дифракционными решетками позволяют производить измерения во всем оптическом диапазоне. Разложение света на спектральные составляющие в них более равномерное, чем в призменных спектрометрах. Штрихи решетки часто наносятся непосредственно на фокусирующие зеркала, что позволяет обойтись без линз. В настоящее время все шире применяются голографические дифракционные решетки, обеспечивающие более высокое разрешение, чем решетки обычного типа. В интерференционных спектрометрах луч света разделяется на два луча, которые следуют разными путями, а затем, снова соединяясь, дают интерференционную картину. Интерферометры обеспечивают самое высокое разрешение и применяются для исследования тонкой и сверхтонкой структуры спектров, а также для измерения относительных длин волн. Интерферометр Фабри – Перо используется как эталон для измерения длин волн в спектрометрах.
В последнее время вместо традиционных призменных и дифракционных приборов в ИК-области применяются фурье-спектрометры. Фурье-спектрометр представляет собой двухлучевой интерферометр с переменной длиной одного плеча. В результате интерференции двух лучей возникает модулированный сигнал, фурье-образ которого дает спектр. Фурье-спектрометры отличаются от обычных большей светосилой и более высоким разрешением. К тому же они позволяют использовать современные компьютерные методы сбора и обработки данных.
Детекторы.
Методы регистрации спектров отличаются большим разнообразием. Очень высокой чувствительностью обладает глаз человека. Однако, будучи высокой для зеленого света (l = 550 нм), чувствительность человеческого глаза быстро падает до нуля на границах инфракрасной и ультрафиолетовой областей. (Заметим, кстати, что комбинационное рассеяние, обычно очень слабое, было обнаружено невооруженным глазом.) Вплоть до 1950-х годов для регистрации спектров широко применялись различные фотопластинки. Их чувствительность позволяла производить измерения во всем диапазоне длин волн от ближней ИК- (1,3 мкм) до вакуумной УФ-области (100 нм и менее). Позже на смену фотопластинкам пришли электронные детекторы и фотодиодные матрицы.
В ИК-области традиционными радиометрическими детекторами были и остаются болометры, радиометры и термоэлементы. Затем появились различные типы малоинерционных и чувствительных фотоэлементов и фотосопротивлений. В видимой и УФ-областях спектра чрезвычайно чувствительны фотоумножители. Они малоинерционны, имеют малый темновой ток и низкий уровень шумов. Применяются также малоинерционные чувствительные многоканальные детекторы. К ним относятся фотодиодные матрицы с микроканальными пластинами и приборы с зарядовой связью. Как и фотопластины, многоканальные детекторы регистрируют сразу весь спектр одновременно; данные с них легко вводятся в компьютер.
Сбор данных и обработка информации.
В настоящее время в спектроскопии применяются компьютерные сбор и обработка данных. Сканирование спектра по длинам волн обычно осуществляется шаговым электродвигателем, который при каждом импульсе от компьютера поворачивает дифракционную решетку на определенный угол. В каждой позиции принятый с детектора сигнал преобразуется в цифровой код и вводится в память компьютера. При необходимости полученная информация может быть выведена на экран дисплея. Для оперативного сравнения данных справочную спектрохимическую информацию, а также эталонные инфракрасные и рамановские спектры обычно хранят на дискетах.
СПЕКТРОСКОПИЧЕСКИЕ МЕТОДЫ
Флуоресцентная спектроскопия.
Флуоресцентная спектроскопия – весьма чувствительный метод анализа химического состава образца, позволяющий обнаруживать следовые количества веществ и даже их отдельные молекулы. В качестве источников возбуждающего излучения особенно эффективны лазеры.
Абсорбционная спектроскопия.
Абсорбционная спектроскопия незаменима при исследованиях в тех областях спектра, где флуоресценция слаба или отсутствует вовсе. Спектр поглощения регистрируется прямым измерением прошедшего через образец света или одним из многочисленных косвенных методов. Для наблюдения слабых и запрещенных переходов применяются длинные или многопроходные кюветы. Использование перестраиваемых лазеров в качестве источников излучения позволяет обойтись без щелевых диафрагм и дифракционных решеток.
Методы регистрации.
Существует ряд чувствительных методов, позволяющих регистрировать изменения, происходящие в исследуемых образцах под действием света. К ним, в частности, относятся индуцированная лазером флуоресценция, лазерная фотоионизация и фотодиссоциация. Оптико-акустический преобразователь измеряет поглощение модулированного света по интенсивности возникающей звуковой волны. Фотогальванические элементы контролируют ток в газовом разряде при исследовании заселенностей высоколежащих уровней, селективно возбуждаемых перестраиваемым лазером.
Спектроскопия насыщения.
Облучение образца интенсивным монохроматическим лазерным излучением вызывает повышенное заселение верхнего уровня перехода и, как следствие, уменьшение поглощения (насыщение перехода). В парах низкого давления селективное насыщение наступает в тех молекулах, скорость которых такова, что благодаря доплеровскому сдвигу достигается резонанс с лазерным излучением. Селективное насыщение практически устраняет доплеровское уширение линий и позволяет наблюдать очень узкие резонансные пики.
Спектроскопия комбинационного рассеяния.
Спектроскопия комбинационного рассеяния – это двухфотонная спектроскопия, основанная на неупругом рассеянии, при котором молекула переходит в нижнее возбужденное состояние, обмениваясь двумя фотонами с полем излучения. В этом процессе поглощается фотон накачки, а испускается рамановский фотон. При этом разность частот двух фотонов равна частоте перехода. В случае равновесной заселенности (заселенность начального состояния больше, чем конечного) частота комбинационного перехода меньше, чем у фотона накачки; она называется стоксовой частотой. В противном случае (заселенность комбинационных уровней инвертирована) испускается «антистоксово» излучение с большей частотой. Поскольку в случае двухфотонного перехода четность начального и конечного состояний должна быть одинакова, комбинационное рассеяние дает информацию, дополнительную по отношению к спектрам ИК-поглощения, которое требует изменения четности.
КАКР.
В методе когерентного антистоксова комбинационного рассеяния (КАКР) используется испускание когерентного света. В процессе КАКР две падающие на образец интенсивные световые волны с частотами n1 и n2 вызывают испускание излучения с частотой 2n1 – n2. Процесс резко усиливается, когда разность частот n1 – n2 равна частоте комбинационного перехода. Это дает возможность измерять разность энергий комбинационных уровней. Метод КАКР отличается высокой чувствительностью.
ПРИКЛАДНАЯ СПЕКТРОСКОПИЯ
Спектральный анализ давно применяется в химии и материаловедении для определения следовых количеств элементов. Методы спектрального анализа стандартизованы, информация о характерных линиях большинства элементов и многих молекул хранится в компьютерных базах данных, что в значительной мере ускоряет анализ и идентификацию химических веществ.
Чрезвычайно эффективным методом контроля за состоянием воздушной среды является лазерная спектроскопия. Она позволяет измерять размер и концентрацию находящихся в воздухе частиц, определять их форму, а также получать данные о температуре и давлении паров воды в верхних слоях атмосферы. Такие исследования проводятся методом лидара (лазерной локации ИК-диапазона).
Спектроскопия открыла широкие возможности для получения информации фундаментального характера во многих областях науки. Так, в астрономии собранные с помощью телескопов спектральные данные об атомах, ионах, радикалах и молекулах, находящихся в звездном веществе и межзвездном пространстве, способствовали углублению наших знаний о таких сложных космологических процессах, как образование звезд и эволюция Вселенной на ранней стадии развития.
До сих пор для определения структуры биологических объектов широко применяется спектроскопический метод измерения оптической активности веществ. По-прежнему при изучении биологических молекул измеряются их спектры поглощения и флуоресценция. Флуоресцирующие при лазерном возбуждении красители используются для определения водородного показателя и ионных сил в клетках, а также для исследования специфических участков в белках. С помощью резонансного комбинационного рассеяния зондируется структура клеток и определяется конформация молекул белков и ДНК. Важную роль сыграла спектроскопия при изучении фотосинтеза и биохимии зрения. Все большее применение находит лазерная спектроскопия и в медицине. Диодные лазеры используются в оксиметре – приборе, определяющем насыщенность крови кислородом по поглощению излучения двух разных частот ближней ИК-области спектра. Изучается возможность использования лазерно-индуцируемой флуоресценции и комбинационного рассеяния для диагностики рака, болезней артерий и ряда других заболеваний.
Зайдель А.Н., Островская Г.В., Островский Ю.И. Техника и практика спектроскопии. М., 1972
Летохов В.С., Чеботарев В.П. Принципы нелинейной лазерной спектроскопии. М., 1975
Ельяшевич М.А. Спектроскопия. Физический энциклопедический словарь. М., 1995
Ответь на вопросы викторины «Физика»