СТАТИКА
СТАТИКА, раздел механики, предметом которого являются материальные тела, находящиеся в состоянии покоя при действии на них внешних сил. В широком смысле слова статика – это теория равновесия любых тел – твердых, жидких или газообразных. В более узком понимании данный термин относится к изучению равновесия твердых тел, а также нерастягивающихся гибких тел – тросов, ремней и цепей. Равновесие деформирующихся твердых тел рассматривается в теории упругости, а равновесие жидкостей и газов – в гидроаэромеханике.
См. ГИДРОАЭРОМЕХАНИКА.
Историческая справка.
Статика – самый старый раздел механики; некоторые из ее принципов были известны уже древним египтянам и вавилонянам, о чем свидетельствуют построенные ими пирамиды и храмы. Среди первых создателей теоретической статики был Архимед (ок. 287–212 до н.э.), который разработал теорию рычага и сформулировал основной закон гидростатики. Родоначальником современной статики стал голландец С.Стевин (1548–1620), который в 1586 сформулировал закон сложения сил, или правило параллелограмма, и применил его в решении ряда задач.
Основные законы.
Законы статики вытекают из общих законов динамики как частный случай, когда скорости твердых тел стремятся к нулю, но по историческим причинам и педагогическим соображениям статику часто излагают независимо от динамики, строя ее на следующих постулируемых законах и принципах: а) законе сложения сил, б) принципе равновесия и в) принципе действия и противодействия. В случае твердых тел (точнее, идеально твердых тел, которые не деформируются под действием сил) вводится еще один принцип, основанный на определении твердого тела. Это принцип переносимости силы: состояние твердого тела не изменяется при перемещении точки приложения силы вдоль линии ее действия.
Сила как вектор.
В статике силу можно рассматривать как тянущее или толкающее усилие, имеющее определенные направление, величину и точку приложения. С математической точки зрения, это вектор, а потому ее можно представить направленным отрезком прямой, длина которого пропорциональна величине силы. (Векторные величины, в отличие от других величин, не имеющих направления, обозначаются полужирными буквами.)
Параллелограмм сил.
Рассмотрим тело (рис. 1,а), на которое действуют силы F1 и F2, приложенные в точке O и представленные на рисунке направленными отрезками OA и OB. Как показывает опыт, действие сил F1 и F2 эквивалентно одной силе R, представленной отрезком OC. Величина силы R равна длине диагонали параллелограмма, построенного на векторах OA и OB как его сторонах; ее направление показано на рис. 1,а. Сила R называется равнодействующей сил F1 и F2. Математически это записывается в виде R = F1 + F2, где сложение понимается в геометрическом смысле слова, указанном выше. Таков первый закон статики, называемый правилом параллелограмма сил.
Равнодействующая сила.
Вместо того чтобы строить параллелограмм OACB, для определения направления и величины равнодействующей R можно построить треугольник OAC, перенеся вектор F2 параллельно самому себе до совмещения его начальной точки (бывшей точки O) c концом (точкой A) вектора OA. Замыкающая сторона треугольника OAC будет, очевидно, иметь ту же величину и то же направление, что и вектор R (рис. 1,б). Такой способ отыскания равнодействующей можно обобщить на систему многих сил F1, F2,..., Fn, приложенных в одной и той же точке O рассматриваемого тела. Так, если система состоит из четырех сил (рис. 1,в), то можно найти равнодействующую сил F1 и F2, сложить ее с силой F3, затем сложить новую равнодействующую с силой F4 и в результате получить полную равнодействующую R. Равнодействующая R, найденная таким графическим построением, представляется замыкающей стороной многоугольника сил OABCD (рис. 1,г).
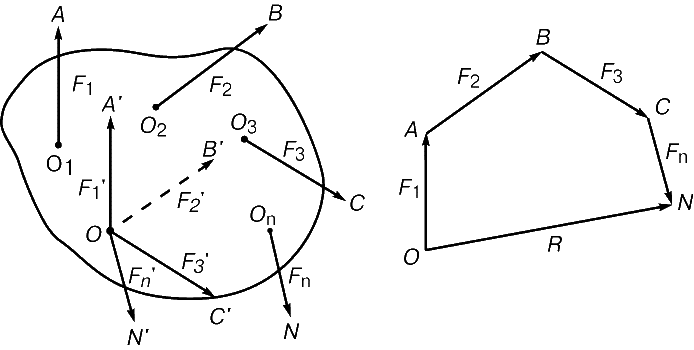
Данное выше определение равнодействующей можно обобщить на систему сил F1, F2,..., Fn, приложенных в точках O1, O2,..., On твердого тела. Выбирается точка O, называемая точкой приведения, и в ней строится система параллельно перенесенных сил, равных по величине и направлению силам F1, F2,..., Fn. Равнодействующая R этих параллельно перенесенных векторов, т.е. вектор, представленный замыкающей стороной многоугольника сил, называется равнодействующей сил, действующих на тело (рис. 2). Ясно, что вектор R не зависит от выбранной точки приведения. Если величина вектора R (отрезок ON) не равна нулю, то тело не может находиться в покое: в соответствии с законом Ньютона всякое тело, на которое действует сила, должно двигаться с ускорением. Таким образом, тело может находиться в состоянии равновесия только при условии, что равнодействующая всех сил, приложенных к нему, равна нулю. Однако это необходимое условие нельзя считать достаточным – тело может двигаться, когда равнодействующая всех приложенных к нему сил равна нулю.
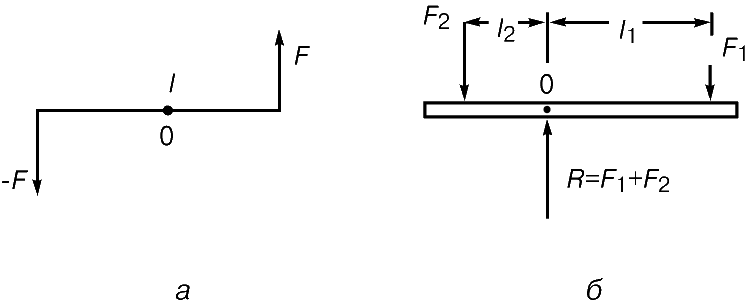
В качестве простого, но важного примера, поясняющего сказанное, рассмотрим тонкий жесткий стержень длиной l, вес которого пренебрежимо мал по сравнению с величиной приложенных к нему сил. Пусть на стержень действуют две силы F и -F, приложенные к его концам, равные по величине, но противоположно направленные, как показано на рис. 3,а. В этом случае равнодействующая R равна F – F = 0, но стержень не будет находиться в состоянии равновесия; очевидно, он будет вращаться вокруг своей средней точки O. Система двух равных, но противоположно направленных сил, действующих не по одной прямой, представляет собой «пару сил», которую можно характеризовать произведением величины силы F на «плечо» l. Значимость такого произведения можно показать путем следующих рассуждений, которые иллюстрируют правило рычага, выведенное Архимедом, и приводят к заключению об условии вращательного равновесия. Рассмотрим легкий однородный жесткий стержень, способный поворачиваться вокруг оси в точке O, на который действует сила F1, приложенная на расстоянии l1 от оси, как показано на рис. 3,б. Под действием силы F1 стержень будет поворачиваться вокруг точки O. Как нетрудно убедиться на опыте, вращение такого стержня можно предотвратить, приложив некоторую силу F2 на таком расстоянии l2, чтобы выполнялось равенство F2l2 = F1l1.
Таким образом, вращение можно предотвратить бесчисленными способами. Важно лишь выбрать силу и точку ее приложения так, чтобы произведение силы на плечо было равно F1l1. Это и есть правило рычага.
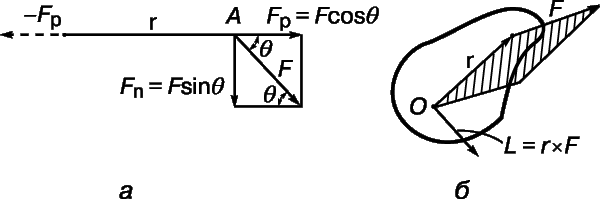
Нетрудно вывести условия равновесия системы. Действие сил F1 и F2 на ось вызывает противодействие в виде силы реакции R, приложенной в точке O и направленной противоположно силам F1 и F2. Согласно закону механики о действии и противодействии, величина реакции R равна сумме сил F1 + F2. Следовательно, равнодействующая всех сил, действующих на систему, равна F1 + F2 + R = 0, так что отмеченное выше необходимое условие равновесия выполняется. Сила F1 создает крутящий момент, действующий по часовой стрелке, т.е. момент силы F1l1 относительно точки O, который уравновешивается действующим против часовой стрелки моментом F2l2 силы F2. Очевидно, что условием равновесия тела является равенство нулю алгебраической суммы моментов, исключающее возможность вращения. Если сила F действует на стержень под углом q, как показано на рис. 4,а, то эту силу можно представить в виде суммы двух составляющих, одна из которых (Fp), величиной F cosq, действует параллельно стержню и уравновешивается реакцией опоры -Fp, а другая (Fn), величиной F sinq, направлена под прямым углом к рычагу. В этом случае крутящий момент равен Fl sinq; он может быть уравновешен любой силой, которая создает равный ему момент, действующий против часовой стрелки.
Чтобы проще было учитывать знаки моментов в тех случаях, когда на тело действует много сил, момент силы F относительно любой точки O тела (рис. 4,б) можно рассматривать как вектор L, равный векторному произведению r ґ F вектора положения r на силу F. Таким образом, L = r ґ F. Нетрудно показать, что если на твердое тело действует система сил, приложенных в точках O1, O2,..., On (рис. 5), то эту систему можно заменить равнодействующей R сил F1, F2,..., Fn, приложенной в любой точке Oў тела, и парой сил L, момент которых равен сумме [r1 ґ F1] + [r2 ґ F2] +... + [rn ґ Fn]. Чтобы убедиться в этом, достаточно мысленно приложить в точке Oў систему пар равных, но противоположно направленных сил F1 и -F1; F2 и -F2;...; Fn и -Fn, что, очевидно, не изменит состояния твердого тела.
Но сила F1, приложенная в точке O1, и сила –F1, приложенная в точке Oў, образуют пару сил, момент которых относительно точки Oў равен r1 ґ F1. Точно так же силы F2 и -F2, приложенные в точках O2 и Oў соответственно, образуют пару с моментом r2 ґ F2, и т.д. Суммарный момент L всех таких пар относительно точки Oў дается векторным равенством L = [r1 ґ F1] + [r2 ґ F2] +... + [rn ґ Fn]. Остальные силы F1, F2,..., Fn, приложенные в точке Oў, в сумме дают равнодействующую R. Но система не может находиться в равновесии, если величины R и L отличны от нуля. Следовательно, условие равенства нулю одновременно величин R и L является необходимым условием равновесия. Можно показать, что оно же является и достаточным, если тело первоначально покоится. Итак, задача о равновесии сводится к двум аналитическим условиям: R = 0 и L = 0. Эти два уравнения представляют собой математическую запись принципа равновесия.
Теоретические положения статики широко применяются при анализе сил, действующих на конструкции и сооружения. В случае непрерывного распределения сил суммы, которые дают результирующий момент L и равнодействующую R, заменяются интегралами  и
и 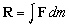 в соответствии с обычными методами интегрального исчисления.
в соответствии с обычными методами интегрального исчисления.
Смокотин Г.Я. Курс лекций по статике. Томск, 1984
Биргер И.А., Мавлютов Р.Р. Сопротивление материалов. М., 1986
Бабенков И.С. Основы статики и сопротивления материалов. М., 1988
Ответь на вопросы викторины «Физика»