ГАЗ

Содержание статьи

• Идеальный газ.
• Средняя кинетическая энергия теплового движения молекул.
• Распределение молекул по скоростям.
• Внутренняя энергия и теплоемкость идеального газа.
• Скорость звука в газе.
• Реальные газы.
• Процессы переноса в газах.

ГАЗ – одно из агрегатных состояний вещества, в котором составляющие его частицы (атомы, молекулы) находятся на значительных расстояниях друг от друга и находятся в свободном движении. В отличие от жидкости и твердого тела, где молекулы находятся на близких расстояниях и связаны друг с другом значительными по величине силами притяжения и отталкивания, взаимодействие молекул в газе проявляется лишь в короткие моменты их сближения (столкновения). При этом происходит резкое изменение величины и направления скорости движения сталкивающихся частиц.

Название «газ» происходит от греческого слова «haos» и было введено Ван Гельмонтом еще в начале 17 в., оно хорошо отражает истинный характер движения частиц в газе, отличающегося полной беспорядочностью, хаотичностью. В отличие, например, от жидкости газы не образуют свободной поверхности и равномерно заполняют весь доступный им объем.

Газообразное состояние, если причислять к нему и ионизованные газы, является самым распространенным состоянием вещества во Вселенной (атмосферы планет, звезды, туманности, межзвездное вещество и т.д.).

Идеальный газ.

Законы, определяющие свойства и поведение газа, легче всего формулируются для случая так называемого идеального газа или газа относительно низкой плотности. В таком газе среднее расстояние между молекулами предполагается большим по сравнению с радиусом действия межмолекулярных сил. Порядок величины этого среднего расстояния можно определить как 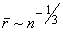, где – n число частиц в единице объема или числовая плотность газа. Если пользоваться приближенной моделью взаимодействия частиц газа, в которой молекулы представляются твердыми упругими шариками диаметром d, то условие идеальности газа записывается как nd³ <<1. Характерный размер молекул газа можно в среднем оценить как d = 3·10^–8 см. Это означает, что газ является идеальным, если n << 3·10²² см^–3. Такому условию заведомо отвечает любой газ (например, воздух), находящийся при нормальных условиях (давление p = 1атм, температура T = 273K), поскольку при этих условиях число молекул в одном кубическом сантиметре газа равно 2,69·10¹⁹см^–3 (число Лошмидта). При фиксированном давлении газа условие идеальности удовлетворяется тем лучше, чем выше температура газа, поскольку плотность газа, как это следует из уравнения состояния идеального газа в этом случае обратно пропорциональна его температуре.

Законы идеального газа были в свое время открыты опытным путем. Так еще в 17 в. был установлен закон Бойля – Мариотта

(1) pV = const,

(2) из которого следует, что изменение объема газа V при постоянной температуре T сопровождается таким изменением его давления p, что их произведение остается постоянной величиной.

Если газ находится в условиях, когда постоянным сохраняется его давление, но меняется температура (такие условия можно осуществить, например, поместив газ в сосуд, закрытый подвижным поршнем), то выполняется закон Гей-Люссака

(2) ,

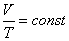т.е. при фиксированном давлении отношение объема газа к его температуре является постоянным. Оба указанных закона объединяются в универсальное уравнение Клапейрона – Менделеева, которое называется также уравнением состояния идеального газа

(3) pV = nRT.

Здесь n – число молей газа, R = 8,317 Дж/моль·K – универсальная газовая постоянная. Молем любого вещества называется такое его количество, масса которого в граммах равна атомной или молекулярной массе вещества М. В свою очередь, молекулярной массой вещества называется отношение массы молекулы этого вещества к так называемой атомной единице массы (а.е.м.), в качестве которой принимается масса равная 1/12 массы атома ¹²С (изотопа углерода с массовым числом 12) (см. ИЗОТОПЫ). При этом 1 а.е.м. = 1,66·10^–27 кг.

Один моль любого вещества содержит одно и то же число молекул, равное числу Авогадро 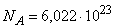моль^–1. Число молей данного количества вещества определяется отношением массы вещества m к его молекулярной массе, т.е. n = m/M .

Используя соотношение n = N/V = nN_A /V, уравнение состояния можно представить в виде, связывающем между собой давление, плотность и температуру

(4) p = nkT,

где вводится величина

k = R/N_A = 1,38·10^–23 Дж/K , которая носит название постоянной Больцмана.

Уравнение состояния в форме (3) или (4) может быть обосновано также методами кинетической теории газов, что позволяет, в частности, придать более отчетливый физический смысл постоянной Больцмана k (см. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ).

Из уравнения состояния идеального газа непосредственно следует закон Авогадро: при одинаковых давлениях и температурах в равных объемах любого газа содержится одинаковое число молекул. Из этого закона вытекает и обратное утверждение: различные газы, содержащие одинаковое число молекул, при одинаковых давлениях и температурах занимают одинаковый объем. В частности, при нормальных условиях моль любого газа занимает объем

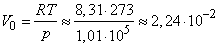м³/моль

Исходя из этого значения легко определить число Лошмидта

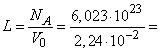2,69·10²⁵ м^–3 = 2,69·10^–19 см^–3

Другой закон, относящийся к смесям идеальных газов, носит название закона Дальтона: давление смеси газов равно сумме парциальных давлений ее компонентов. Парциальным давлением какого либо газа (компонента газовой смеси) называется при этом давление, которое оказывал бы этот газ, если бы он один занимал весь объем, занимаемый смесью.

Средняя кинетическая энергия теплового движения молекул.

Уравнение состояния идеального газа в форме (3) или (4) может быть обосновано и методами кинетической теории газов. На основе кинетического подхода сравнительно просто выводится выражение для давления идеального газа в сосуде, которое получается как результат усреднения импульсов молекул, передаваемых стенке сосуда при многочисленных соударениях молекул со стенкой. Величина получаемого при этом давления определяется как

(5) ,

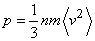Где бv ²с – среднее значение квадрата скорости молекул, m – масса молекулы.

Средняя кинетическая энергия молекул газа (в расчете на одну молекулу) определяется выражением

(6)

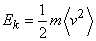
Кинетическая энергия поступательного движения атомов и молекул, усредненная по огромному числу беспорядочно движущихся частиц, является мерилом того, что называется температурой. Если температура T измеряется в градусах Кельвина (К), то связь ее с E_k дается соотношением

(7)

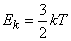
Это соотношение позволяет, в частности, придать более отчетливый физический смысл постоянной Больцмана

k = 1,38·10^–23 Дж/K, которая фaктически является переводным коэффициентом, определяющим, какая часть джоуля содержится в градусе.

Используя (6) и (7), находим, что (1/3)m бv²с = kT. Подстановка этого соотношения в (5) приводит к уравнению состояния идеального газа в форме

p = nkT, которое уже было получено из уравнения Клапейрона – Менделеева (3).

Из уравнений (6) и (7) можно определить значение средне-квадратичной скорости молекул

(8)

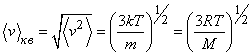
Расчеты по этой формуле при Т = 273К дают для молекулярного водорода бvс_кв = 1838 м/с, для азота – 493 м/с, для кислорода – 461 м/с и т.д.

Распределение молекул по скоростям.

Приведенные выше значения бvс_кв позволяют составить представление о порядке величины среднего значения тепловых скоростей молекул для различных газов. Разумеется, не все молекулы движутся с одинаковыми скоростями. Среди них есть определенная доля молекул с малыми значениями скорости и, наоборот, некоторое число достаточно быстрых молекул. Однако, большая часть молекул обладает скоростями, значения которых группируются относительно наиболее вероятной при данной температуре величины, которая не очень существенно отличается от значений, даваемых формулой (8). Такое распределение молекул по скоростям устанавливается в газе в результате обмена импульсом и энергией при многочисленных столкновениях молекул между собой и со стенками сосуда, Вид этого универсального (не меняющегося во времени) распределения молекул по скоростям, соответствующего состоянию теплового равновесия в газе, был впервые теоретически установлен Максвеллом. С помощью распределения Максвелла определяется относительная доля молекул, абсолютные скорости которых лежат в некотором узком интервале значений dv.

(9)

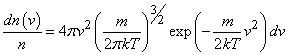
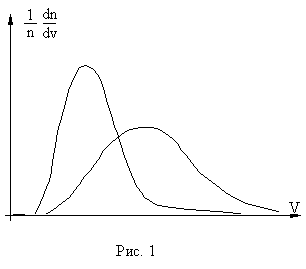
Вид распределения dn/ndv, описываемого выражением (9), для двух различных температур (T₂ > T₁) представлен на рис.1.

С помощью максвелловского распределения можно вычислить такие важные характеристики газа как средняя, среднеквадратичная и наиболее вероятная скорость теплового движения молекул, рассчитать среднее число столкновений молекул со стенкой сосуда и т.д. Средняя тепловая скорость молекул, например, которая представляет собой фактически средне-арифметическую скорость, определяется при этом формулой

(10)

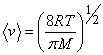
Наиболее вероятная скорость молекул, соответствующая максимуму кривых, представленных на рис. 1, определена как

(11)

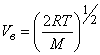
Значения скоростей, определяемых формулами (8), (10) и (11), оказываются близкими по величине. При этом

(12) бvс = 0,93 бvс_кв, n_в = 0,82бvс_кв

Внутренняя энергия и теплоемкость идеального газа.

Чтобы изменить состояние некоторого заданного объема газа (например, нагреть или охладить его), надо либо совершить над ним механическую работу, либо передать ему некоторое количество тепла за счет контакта с другими телами. Количественно эти изменения выражаются с помощью первого начала термодинамики, которое отражает важнейший закон природы: сохранение механической и тепловой энергии тела. Формулировку первого начала для бесконечно малого квазистатического процесса можно представить в виде (см. ТЕРМОДИНАМИКА).

(13) dQ = dU + dA

Здесь dQ – элементарное количество тепла, передаваемое телу, dU – изменение его внутренней энергии,

dA = pdV – элементарная работа, совершаемая газом при изменении его объема (эта работа равна с обратным знаком элементарной работе, совершаемой внешними силами над газом). Обозначение dU соответствует полному дифференциалу от переменной U. Это означает, что приращение внутренней энергии при переходе газа из некоторого состояния 1 в состояние 2 можно представить в виде интеграла

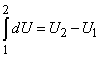
Обозначения dQ и dA означают, что в общем случае интеграл от них нельзя представить в виде разности соответствующих значений в конечном и начальном состоянии газа, поэтому интегрирование (13) по всему процессу приводит к соотношению

Q = U₂ – U₁ + A

Вводится понятие теплоемкости газа как количества тепла, которое нужно сообщить газу, чтобы повысить его температуру на один градус Кельвина. Тогда по определению

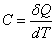
Далее под С подразумевается теплоемкость, отнесенная к одному молю газа, или молярная теплоемкость. Внутренняя энергия U также определена для одного моля газа. Если газ нагревается при постоянном объеме (изохорический процесс), т.е. совершаемая газом работа равна нулю, то

(14)

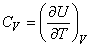
Если состояние газа меняется при постоянном давлении (изобарический процесс), то в соответствии с (13)

(15)

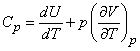
Использование уравнение состояния идеального газа (3) при v = 1 дает

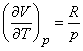
Следовательно, молярные теплоемкости идеального газа при постоянном давлении и при постоянном объеме связаны соотношением

(16) C_p = C_v + R

Внутренняя энергия газа, в общем случае, состоит из кинетической энергии поступательного и вращательного движения молекул, энергии внутреннего (колебательного) движения атомов в молекуле, а также потенциальной энергии взаимодействия молекул. В случае идеального газа вкладом последнего слагаемого в полную энергию можно пренебрегать.

В классической статистической механике доказывается так называемая теорема о равномерном распределении кинетической энергии по степеням свободы молекул, согласно которой на каждую степень свободы молекулы в состоянии теплового равновесия в среднем приходится энергия, равная (1/2)kT.

Для газов, состоящих из одноатомных молекул, (например, инертные газы) средняя кинетическая энергия, приходящаяся на один атом, определена соотношением (7), поскольку она соответствует лишь поступательному движению атомов, (3 степени свободы). В этом случае

,

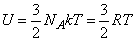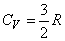
Существенно, что для идеального газа одноатомных молекул внутренняя энергия зависит только от температуры и не зависит от объема.

Для линейных двухатомных молекул число степеней свободы равно пяти (на одну степень свободы меньше, чем для системы двух независимых атомов, поскольку в молекуле эти атомы связаны жесткой связью) Дополнительные две степени свободы описывают вращательное движение молекулы относительно двух взаимно-перпендикулярных осей. При этом

,

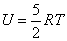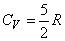
Если атомы в молекуле совершают еще и колебания, то, согласно классической теории, наличие колебательного движения вносит вклад в среднюю энергию молекулы, равный kT (по kT/2, приходящийся на кинетическую и потенциальную энергии колебаний. Тогда в случае молекулы, образованной из 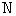атомов,

,

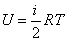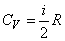
где i = n_пост + n_вращ + 2n_кол – полное число степеней свободы молекулы. При этом n_пост = 3. Для линейной молекулы n_вращ = 2, n_кол = 3N – 5. Для всех других молекул n_вращ = 3, n_кол = 3N – 6.

Классическая теория, в основном, правильно описывает тепловые явления в газе в некоторых узких интервалах температур, однако температурная зависимость теплоемкости в целом, наблюдаемая в эксперименте, ведет себя далеко не так, как предсказывает классическая теория. Это несоответствие теории и эксперимента было понято только с появлением квантовой теории теплоемкости, основанной на представлении о дискретности вращательных и колебательных уровней молекул. При низких температурах наблюдается только поступательное движение молекул. С ростом температуры все большее число молекул вовлекается во вращательное движение. Если средняя тепловая энергия kT заметно превышает энергию первого вращательного уровня, в молекуле возбуждено уже много вращательных уровней. В этом случае дискретность уровней становится несущественной и теплоемкость равна своему классическому значению. Аналогичная ситуация имеет место и с возбуждением колебательных степеней свободы. Квантовая теория полностью объясняет характер температурной зависимости теплоемкости, ее непрерывный характер, отличающийся постепенным вовлечением в «игру» различных степеней свободы молекул.

Изотермические и адиабатические процессы в газе. Наряду с процессами изменения параметров газа, происходящими при постоянном объеме или при постоянном давлении, возможны изотермические (T = const, внутренняя энергия газа остается неизменной) и адиабатические (без отвода и подвода тепла к газу) процессы. В первом случае все подводимое к газу тепло расходуется на механическую работу, а изменение давления и объема для одного моля газа удовлетворяет условию pV = PT = const. В p-V координатах на плоскости соответствующие зависимости образуют семейство изотерм.

Для адиабатического процесса (dQ = 0) из (13) и (14) следует

C_VdT + pdV = 0

Уравнение состояния идеального газа дает

dT = R^–1(pdV + Vdp).

Используя (16), уравнение адиабатического процесса можно представить в дифференциальной форме

(17) gpdv + Vdp = 0, где g = С_р/C_V– отношение теплоемкостей при постоянном давлении и постоянном объеме, называемое адиабатической постоянной. Дифференциальному соотношению (17) при g = const соответствует уравнение адиабаты pV^g = const

или

(18) TV^{g – 1} = const

Так как g > 1, то из (18) следует, что при адиабатическом сжатии газ нагревается, а при расширении – охлаждается. Это явление находит применение, например, в дизельных двигателях, где горючая смесь воспламеняется за счет адиабатического сжатия.

Скорость звука в газе.

Из гидрогазодинамики известно, что скорость звука в сплошной среде определяется соотношением

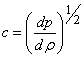
В первоначальных теориях (Ньютон) считалось, что давление и плотность связаны обычным уравнением состояния, т.е. p/r = соnst. Это соответствует предположению, что разности температур между сгущениями и разрежениями газа в звуковой волне мгновенно выравниваются, т.е. распространение звука является изотермическим процессом. В этом случае формула Ньютона для скорости звука принимает вид

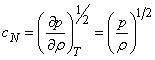
Эта формула, однако, противоречила эксперименту. Лаплас первым понял, что колебания плотности и связанные с этим колебания температуры в звуковой волне происходят настолько быстро, что для таких процессов теплообмен несущественен и выравнивания температур не происходит. Это означает, что вместо уравнения изотермы надо пользоваться уравнением адиабаты. Тогда выражение для скорости звука принимает вид

(19)

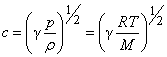
Скорость звука в газе имеет тот же порядок величины, что и средняя тепловая или средне-квадратичная скорости молекул. Это понятно, поскольку возмущения в звуковой волне передаются молекулами, движущимися с тепловыми скоростями. Для молекулярного азота, например, g = 1,4 и скорость звука при T = 273К равна 337 м/с. Средняя тепловая скорость молекул азота бvс при тех же условиях равна 458 м/с.

Реальные газы.

С ростом давления и уменьшением температуры состояние газа начинает все больше отклоняться от идеальности. Эксперимент показал, например, что для азота N₂ при температуре T = 273K и давлении p =100 атм, ошибка в определении объема газа, если пользоваться уравнением состояния (3), может достигать 7%. Это связано с тем, что при таком давлении молекулы газа в среднем удалены друг от друга на расстояние, которое только вдвое больше их собственных размеров, а собственный объем молекул лишь в 20 раз меньше объема газа. При дальнейшем повышении давления становится все более существенным учет влияния на поведение газа как сил межмолекулярного взаимодействия, так и собственного объема молекул.

Пока отклонения от идеальности малы, их можно учесть с помощью так называемого вириального разложения – разложения давления в ряд по степеням плотности молекул в объеме N/V

(20) ,

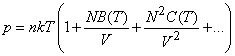где B(T), C(T) – так называемые вириальные коэффициенты, зависящие от температуры и характеризующие влияние межмолекулярного взаимодействия. Для учета более сильных отклонений предложено много полуэмпирических и эмпирических уравнений состояния реальных газов, из которых наиболее часто используется уравнение Ван-дер-Ваальса.

Уравнение состояния неидеального газа – уравнение Ван-дер-Ваальса записывается для одного моля газа в виде

(21)

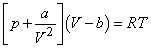
В нем учитывается как собственный объем молекул (постоянная b), так и влияние сил притяжения между молекулами (постоянная a). Из этого уравнения вытекает, в частности, существование наблюдаемой на опыте критической температуры и критического состояния. Критическое состояние характеризуется значением T_k и соответствующими ему значениями p_k и V_k. При критической температуре T_k исчезает различие между разными состояниями вещества. Выше этой температуры переход от жидкости к газу либо, наоборот, от газа к жидкости оказывается непрерывным.

Процессы переноса в газах.

Если в газе создается какая-либо неоднородность его параметров (например, разные температуры газа или разные концентрации компонентов газовой смеси в разных частях сосуда), то возникают отклонения состояния газа от равновесия, которые сопровождаются переносом энергии (теплопроводность) или массы компонентов смеси (диффузия) из одной части сосуда в другую. При различии в скоростях перемещения разных слоев газа (например, при течении газа в трубе) возникает поперечный перенос импульса (вязкость). Все эти явления объединяются одним общим названием процессы переноса. При их описании особенно важным оказывается учет характера столкновений молекул в газе. Порядок величины соответствующих коэффициентов переноса (кинетических коэффициентов) и характер зависимости их от основных параметров дается элементарной кинетической теорией газа, основанной на модели молекул в виде твердых упругих шаров и на концепции средней длины свободного пробега молекул. Для переноса энергии в газе принимается

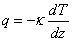
где q – плотность потока энергии (поток тепла), k – коэффициент теплопроводности, dT/dz – градиент температуры в направлении оси z.

Сила вязкого трения, возникающая между двумя слоями в движущемся газе, если имеется поперечное распределение скорости газа u(x), имеет вид

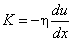
Наконец, если в бинарной газовой смеси молекул с близкой массой компонентов задано распределение плотности одного из компонентов n₁(z), то диффузионный поток молекул компонента в направлении z записывается в виде

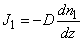
Коэффициенты переноса в этих соотношениях: коэффициенты теплопроводности k, вязкости h и самодиффузии D, получаемые методами элементарной кинетической теории, записываются в виде,

(22) , ,

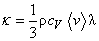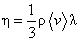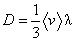
где l – средняя длина свободного пробега молекул, бvс – средняя тепловая скорость молекул. Поскольку 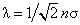, где s – поперечное сечение столкновений молекул. коэффициенты теплопроводности и вязкости не зависят от плотности (или от давления) газа, в то время как коэффициент диффузии D ~ 1/p.

В элементарной теории численные коэффициенты в выражениях (22) оказываются одинаковыми. Точная теория для модели твердых упругих шаров (s = сonst) дает h = 0,5бvс l, k = 2,5(R/M)h,

rD = 1,2h

Более реалистические модели взаимодействия молекул в газе вносят изменения в характер зависимости коэффициентов переноса от температуры, что позволяет обеспечить лучшее совпадение теории с результатами экспериментальных измерений этих коэффициентов.

Владимир Жданов