ВАНТ-ГОФФА ПРАВИЛО

ВАНТ-ГОФФА ПРАВИЛО. Почти все химические реакции при повышении температуры идут быстрее. Зависимость скорости реакции от температуры описывается уравнением Аррениуса:

k = Ae^–Ea/RT, где k – константа скорости реакции, А – не зависящая от температуры константа (ее называют предэкспоненциальным множителем), Е_а– энергия активации, R – газовая постоянная, Т – абсолютная температура. В школьных учебниках зависимость скорости реакции от температуры определяют в соответствии с так называемым «правилом Вант-Гоффа», которое в 19 в. сформулировал голландский химик Якоб Вант-Гофф. Это чисто эмпирическое правило, т.е. правило, основанное не на теории, а выведенное из опытных данных. В соответствии с этим правилом, повышение температуры на 10° приводит к увеличению скорости в 2–4 раза. Математически эту зависимость можно выразить уравнением v₂v₁ = g (T₂^{– T}₁^)/10, где v₁ и v₂– скорости реакции при температурах Т₁ и Т₂; величина g называется температурным коэффициентом реакции. Например, если g = 2, то при Т₂– Т₁ = 50^оv₂/v₁ = 2⁵ = 32, т.е. реакция ускорилась в 32 раза, причем это ускорение никак не зависит от абсолютных величин Т₁ и Т₂, а только от их разности.

Однако из уравнения Аррениуса следует, что температурный коэффициент реакции зависит как от энергии активации, так и от абсолютной температуры. Для данной реакции с определенным значением Е_а ускорение при повышении температуры на 10° будет тем больше, чем ниже температура. Это почти очевидно и без расчетов: повышение температуры от 0 до 10° С должно сказаться на скорости реакции значительно сильнее, чем такое же повышение температуры, например, от 500 до 510° С.

С другой стороны, для данного температурного интервала ускорение реакции будет тем сильнее, чем больше ее энергия активации. Так, если энергия активации реакции мала, то такая реакция идет очень быстро, и при повышении температуры на 10° С ее скорость почти не изменяется. Для таких реакций температурный коэффициент намного меньше 2. Для реакций же с большой энергией активации, которые при невысоких температурах идут медленно, ускорение при повышении температуры на 10° С может значительно превысить 4-кратное.

Например, реакция диоксида углерода со щелочным раствором с образованием гидрокарбонат-иона (СО₂ + ОН® НСО₃^–) имеет энергию активации 38,2 кДж/моль, поэтому при повышении температуры, например, от 50 до 60° С эта реакция ускорится всего в 1,5 раза. В то же время реакция распада этилбромида на этилен и бромоводород (С₂Н₅Вr ® С₂Н₄ + НВr) с энергией активации 218 кДж/моль ускорится при повышении температуры от 100 до 110^oС в 6,3 раза (правда, в этом интервале температур реакция идет очень медленно). Кинетика реакции атомов водорода с этаном H + C₂H₆ ® H₂ + C₂H₅ была изучены в широком температурном интервале – от 300 до 1100 К (27–827° С). Для этой реакции E_а = 40,6 кДж/моль. Следовательно, повышение температуры на 10° вызовет увеличение скорости реакции в 1,7 раза в интервале 300–310 K и только в 1,04 раза в интервале 1090–1100 K. Так что при высоких температурах скорость этой реакции практически не зависит от температуры. А для реакции присоединения атома водорода к двойной связи H + C₂H₄ ® C₂H₅ энергия активации мала (E_а = 3,4 кДж/моль, так что ее скорость слабо зависит от температуры в широком температурном интервале. И только при температурах намного ниже 0° С начинает сказываться наличие активационного барьера.

Подобных примеров можно привести множество. Очевидно, что правило Вант-Гоффа противоречит не только уравнению Аррениуса, но и многим экспериментальным данным. Откуда же оно взялось и почему нередко выполняется?

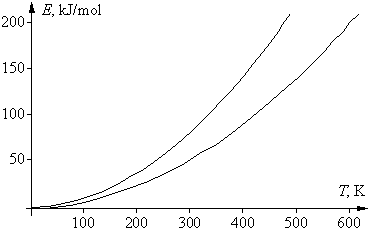
Если в приведенном выше математическом выражении для правила Вант-Гоффа подставить вместо скоростей v₁ и v₂ для данной реакции их зависимости от температуры, в соответствии с уравнением Аррениуса, то после сокращения предэкспоненциальных множителей получим следующее выражение: g = v_T +10/v_T = е^–Еа/R(Т+10)/е^–Еа/RТ = е^{(Еа/R)[1/Т – 1/(T+10)]}. Логарифмироване этого уравнения дает: lng = (E_а/R)[1/T – 1/(T + 10)], откуда Еа = Rlng T(T + 10)/10 = 0,83lngT(T + 10). Энергия активации не является функцией температуры, эта зависимость нужна лишь для удобства последующего анализа. Последнее уравнение – это уравнение параболы, в котором физический смысл имеют только положительные значения. Соответствующая диаграмма ограничена двумя ветвями параболы: при g = 2 получаем Е_а = 0,58Т(Т + 10), при g = 4 получаем Е_а = 1,16Т(Т + 10). К тем же формулам приходим и при использовании десятичных логарифмов. Соответствующие графики двух парабол, для значений g 2 и 4, приведены на рисунке. Их физический смысл заключается в том, что области выполнения правила Вант-Гоффа соответствует только область между параболами. Таким образом, существуют только определенные соотношения между энергией активации реакции и температурой ее проведения, при которых правило Вант-Гоффа выполняется. Ниже нижней ветви температурный коэффициент g < 2, тогда как выше верхней ветви g > 4.

Если посмотреть, какие реакции «укладываются» в указанную довольно узкую область, то окажется, что все эти реакции идут не слишком быстро и не слишком медленно, а с удобной для измерения (при данной температуре) скоростью. Скорость только таких реакций и могли изучать химики во времена Вант-Гоффа. Например, если энергия активации была невелика (меньше 50 кДж/моль), то такая реакция при комнатной температуре заканчивалась за 1–2 секунды; поэтому для изучения ее кинетики следовало значительно понизить температуру, чтобы реакция проходила не быстрее, чем за 10–20 минут. Только в этом случае химики 19 в. успевали отбирать пробы по ходу реакции и анализировать изменение в них концентрации реагентов. Других способов изучения скорости реакции в то время не было. Если это не удавалось (например, водный раствор замерзал), то скорость такой реакции не изучали. Если же энергия активации реакции была велика и при комнатной температуре она шла слишком медленно (многие сутки, или даже недели), то температуру повышали, чтобы реакция шла с удобной для измерения скоростью. И здесь были свои ограничения – например, раствор мог закипеть, т.е. в любом случае исследователи фактически «подстраивали» изучаемую реакцию под область между двумя параболами.

Сейчас химики имеют возможность с помощью различных приборов экспериментально изучать и очень быстрые (идущие в микросекундной области), и очень медленные реакции, для которых температурный коэффициент может быть значительно меньше 2 или значительно больше 4. Поэтому правило Вант-Гоффа, которое, в отличие от уравнения Аррениуса, не имеет четкого физического смысла, представляет лишь чисто исторический интерес и в современной науке не используется. В подавляющем большинстве учебников и монографий по химической кинетике, а также в 5-томной Химической Энциклопедии это правило даже не упоминается. И, тем не менее, если изучаемая реакция идет с удобной для измерения скоростью, например, заканчивается за 30–40 мин, а энергия активации ее еще не измерена, то для предварительной грубой оценки зависимости скорости такой реакции от температуры можно использовать правило Вант-Гоффа. Поэтому это правило приводится во всех школьных учебниках химии.

Илья Леенсон