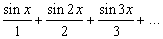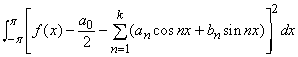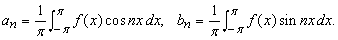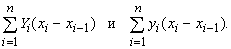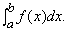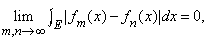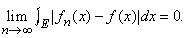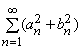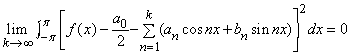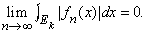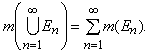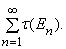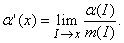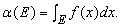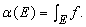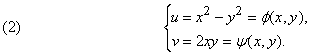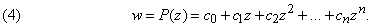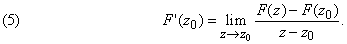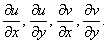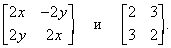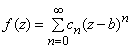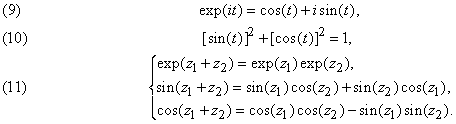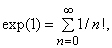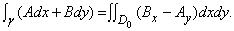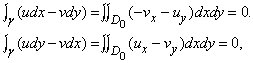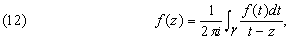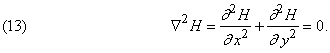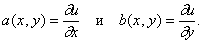ФУНКЦИЙ ТЕОРИЯ

Содержание статьи

• ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
• МЕРА И ИНТЕГРИРОВАНИЕ
• Теория Лебега.
• Основные предельные теоремы.
• Аксиоматический подход.
• Построение внешних мер.
• Дифференцирование.
• Интеграл Даниеля.
• ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
• КЛАССИЧЕСКАЯ ТЕОРИЯ
• СОВРЕМЕННАЯ ТЕОРИЯ
• ПРИЛОЖЕНИЯ
• В естественных науках.
• В чистой математике.

ФУНКЦИЙ ТЕОРИЯ, раздел математики, занимающийся изучением свойств различных функций. Теория функций распадается на две области: теорию функций действительного переменного и теорию функций комплексного переменного, различие между которыми настолько велико, что обычно их рассматривают порознь. Не вдаваясь в детали, можно сказать, что по существу речь идет о различии, с одной стороны, в детальном изучении основных понятий математического анализа (таких, как непрерывность, дифференцирование, интегрирование и т.п.), а с другой стороны, в теоретическом развитии анализа конкретных функций, представимых степенными рядами. Одним из достижений теории функций действительного переменного стало создание хорошей теории интегрирования, которую мы рассмотрим ниже. См. также АНАЛИЗ В МАТЕМАТИКЕ; МАТЕМАТИЧЕСКИЙ АНАЛИЗ; ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ; ФУНКЦИЯ; ЧИСЛО; РЯДЫ; МНОЖЕСТВ ТЕОРИЯ; ТОПОЛОГИЯ.

ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО

Функции, используемые в элементарном анализе, задаются формулами. Их графики обычно можно начертить, не отрывая карандаш от бумаги, как, например, график функции y = sinx, или они состоят из отдельных кусков, обладающих этим свойством, как, например, график функции y = tgx (рис. 1). Первоначально, когда строгое определение непрерывности отсутствовало, все функции, графики которых состоят из одного куска, считались обязательно непрерывными. Например, считалось, что непрерывной можно считать функцию, график которой не может лежать по обе стороны от прямой, не пересекая ее. Иначе говоря, непрерывная функция, принимая какие-либо два значения, непременно принимает и все промежуточные значения. Однако нетрудно найти функции, которые, хотя и заданы формулами и обладают указанным свойством, ведут себя не как непрерывные. Например, функция f(x) = sin(1/x) при x № 0 и f(0) = 0 (рис. 2) обладает свойством, о котором идет речь, однако, по мнению многих, не является непрерывной. Можно построить еще более удивительные примеры функций, принимающих действительное значение на любом сколь угодно малом интервале, но тем не менее не являющихся непрерывными. Графики таких функций не только невозможно начертить, но иногда даже и четко представить себе. С другой стороны, работы Ж.Фурье (1768–1830) и П.Дирихле (1805–1859), связанные с рядами Фурье показали, что некоторые заведомо разрывные функции задаются формулами, по крайней мере, если в число последних включить бесконечные ряды.

Возникшие при этом логические трудности были постепенно преодолены с помощью приема, типичного для теории функций: понятиям «функция» и «непрерывность» были даны строгие определения и исследованы вытекающие из них логические следствия. Оказалось, что эти следствия не находятся в точном соответствии с интуицией, о чем свидетельствуют приведенные примеры. Один из самых знаменитых примеров такого рода был предложен К.Вейерштрассом (1815–1897) – пример непрерывной, но нигде (ни в одной точке) не дифференцируемой функции. У математика, столкнувшегося с таким примером, может возникнуть много вопросов, например, «У каких непрерывных функций существуют производные?», или «Как можно изменить понятие производной, чтобы оно стало применимым к большинству непрерывных функций?», или «Какими дополнительными свойствами обладают недифференцируемые функции?». Проблемами такого рода и занимается теория функций действительного переменного.

Первое, что требуется от теории функций, – дать определение понятия «функции». Мы не станем приводить здесь самое общее из возможных определений, а просто скажем, что функция – это правило, которое каждому числу (или каждой точке) из данного множества ставит в соответствие другое число, называемое значением функции в этой точке. (См. ФУНКЦИЯ.) Например, одна функция ставит в соответствие каждому действительному числу его квадрат, другая ставит в соответствие каждому положительному действительному числу его логарифм, третья функция ставит в соответствие каждому рациональному числу, записанному в виде несократимой дроби, знаменатель этой дроби. Все названные функции имеют различные области определения; областью определения функции называется множество точек, на котором она определена.

Функция называется непрерывной в точке, если любому бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции. Функция, непрерывная во всех точках области определения, называется непрерывной. Например, функция, принимающая в точке x значение x², непрерывна; но функция, принимающая в точке x значение, равное ближайшему к x целому числу, не превосходящему x, непрерывной не является. В самом деле, значение этой функции изменяется скачком с 0 на 1, когда x изменяется от значения, меньшего 1/2 на сколь угодно малую величину, до значения, большего 1/2, на сколь угодно малую величину. На формальном математическом языке можно сказать, что функция f, принимающая значения f(x), непрерывна в точке y в том случае, если для любого положительного числа e найдется такое число d, что для всех точек x из области определения f(x), удовлетворяющих условию |x – y| < d, выполняется неравенство |f(x) – f(y)| < e.

Можно показать, что непрерывные функции, областями определения которых являются подмножества множества действительных чисел, обладают многочисленными свойствами, некоторые из которых интуитивно очевидны, а некоторые – нет. Например, сумма или произведение непрерывных функций также непрерывны. Если непрерывная функция в некоторой точке положительна, то всегда найдется достаточно малая ее окрестность, в которой она останется положительной. Если непрерывная функция принимает в двух точках различные значения a и b, то в промежуточных точках она принимает все значения, заключенные между a и b. Из последнего свойства можно заключить, например, что если растянутой резинке дать сжаться таким образом, чтобы она оставалась прямолинейной (не провисала), то одна из точек на ней останется неподвижной.

Функции, с которыми приходится иметь дело в математическом анализе, как правило, всюду непрерывны в области их определения, за исключением, быть может, отдельных изолированных точек. В то же время было построено много примеров разных функций как разрывных, так и нет, обладающих свойствами, противоречащими интуиции.

Хотя сумма двух непрерывных функций непрерывна, а следовательно, непрерывна и сумма любого конечного числа непрерывных функций, аналогичное утверждение для бесконечных сумм неверно. Например, бесконечная сумма

является периодической (с периодом 2p) разрывной функцией, принимающей значения 0 при x = 0 и (1/2)(p – x) в интервале от 0 до 2p (рис. 3). Для того, чтобы ряд из непрерывных функций обязательно имел непрерывную сумму, необходимы более сильные условия, чем сходимость в каждой точке общей области определения функций. С другой стороны, предел непрерывных функций или повторный предел имеет все основания считаться формулой, и один из разделов теории функций занимается проблемой выяснения, какого рода функции представимы такими формулами. Согласно классификации разрывных функций, предложенной Р.Бэром (около 1899) непрерывные функции принадлежат 0-му классу, пределы непрерывных функций принадлежат 1-му классу и т.д. Функция, график которой изображен на рис. 3, принадлежит 1-му классу; функция

принимающая значения 1 при рациональных x и 0 при иррациональных x, принадлежит 2-му классу. Существуют функции, принадлежащие классу сколь угодно большого порядка, а также функции, вообще не принадлежащие какому-либо классу Бэра.

Были построены примеры, показывающие, что непрерывная функция необязательно должна иметь производную в каждой точке. У.Дини в 1877 предложил новое определение производной, применимое к любой функции и позволяющее заменить обычную производную во многих приложениях. Анализ функций с помощью различных обобщений производных позволил обнаружить многие свойства разрывных функций и показал, что большинство функций общего вида обладают внутренней симметрией.

Одним из важных классов функций являются так называемые монотонные функции, т.е. либо возрастающие, либо убывающие. (Возрастающей называется функция, которая бóльшим значениям переменной из области определения ставит в соответствие бóльшие значения функции.) Разность двух возрастающих функций обладает свойством, известным под названием «ограниченная вариация», что означает, что график такой разности не может совершать слишком сильные колебания; каждая функция ограниченной вариации записывается в виде разности двух монотонных функций. Лишь те функции, которые «сшиты» из конечного числа монотонных функций, могут быть достаточно убедительно представлены в графическом виде. Наконец, монотонная функция почти всюду дифференцируема.

Словам «почти всюду» можно придать точный смысл, который восходит к теории интегрирования, но можно это сделать и независимо от теории. Множество действительных чисел называется множеством меры нуль, если его можно покрыть счетным семейством интервалов сколь угодно малой суммарной длины. Например, множество рациональных чисел имеет меру нуль, так как оно счетно: при любом сколь угодно малом числе e мы можем покрыть первое рациональное число интервалом длиной e/2, второе число – интервалом длиной e/4, третье – интервалом длиной e/8 и т.д.; в результате все множество окажется покрыто интервалами (частично пересекающимися), суммарная длина которых составляет e(1/2 + 1/4 + 1/8 +...) = e. Множество точек, в которых монотонная функция не имеет производной, является множеством меры нуль. В теории функций имеется много теорем, утверждающих, что некоторая функция обладает каким-либо свойством всюду, кроме множества меры нуль или множества, «малого» в том или ином смысле.

Хотя не все непрерывные функции дифференцируемы, многие дифференцируемые функции встречаются на практике, и все дифференцируемые функции непрерывны. В качестве примера свойств дифференцируемых функций приведем теорему Ролля, которая утверждает, что если действительная функция непрерывна на некотором отрезке, имеет в каждой его точке производную, а на концах принимает равные значения, то на этом интервале существует хотя бы одна точка, в которой производная этой функции равна нулю. Геометрический смысл этой теоремы состоит в том, что на графике такой функции существует такая точка, принадлежащая заданному интервалу, что в ней касательная к графику параллельна оси x. Отсюда нетрудно вывести так называемую теорему о среднем: если функция f непрерывна и дифференцируема на отрезке и a и b – две точки, принадлежащие этому отрезку, то

f(b) – f(a) = (b – a)f ў(c),

где c – некоторая точка между a и b.

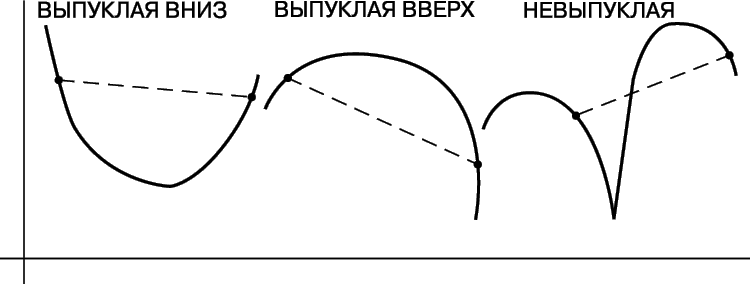
Другим важным свойством действительной функции является выпуклость. Говорят, что функция выпукла вниз, если дуга ее графика, заключенная между любыми двумя точками, лежит ниже соединяющей их хорды (рис. 4). Можно показать, что функция выпукла вниз, если для любого интервала, стягивающая его хорда, находится выше кривой. Выпуклая вниз функция дифференцируема всюду, кроме, быть может, счетного числа «изломов», а ее производная сама является возрастающей функцией.

Еще одним типичным примером задач теории функций действительного переменного может служить задача аппроксимации данной функции функциями определенного рода. Если аппроксимирующие функции – суммы синусов или косинусов, то это центральная задача гармонического анализа; на практике здесь часто имеется ввиду представление данного колебания суммой гармоник. Задача приближения непрерывных функций многочленами возникает во многих практически важных областях, например, при проектировании механических устройств для вычерчивания (приближенного) графика заданной кривой или при создании быстродействующих компьютерных программ для вычисления значений сложных функций. Согласно доказанной Вейерштрассом в 1885 теореме о приближении функций, любую функцию, непрерывную на замкнутом интервале, можно сколь угодно точно аппроксимировать многочленами либо суммами синусов и косинусов. Слова «сколь угодно точно» здесь означают, что разность между данной функцией и функциями ее аппроксимирующими может быть сделана сколь угодно малой равномерно на всем интервале (если графики данной функции и аппроксимирующих функций начертить на бумаге, то при достаточно точной аппроксимации эти графики будут неотличимы).

Теория функций занимается также изучением свойств функций, размерности области определения которых более единицы (функции нескольких переменных). Отсюда уже можно перейти к функциям, областями определения которых служат разного рода абстрактные пространства, и даже к функциям, значения которых также принадлежат многомерным пространствам (таковы, например, векторные поля в физике) или абстрактным пространствам. Таким образом, теория функций незаметно переходит, с одной стороны, в функциональный анализ, а с другой – в топологию.

МЕРА И ИНТЕГРИРОВАНИЕ

Теория меры и интегрирования является важным разделом общей теории математических функций, берущей начало с работ А.Лебега (1906) по теории интеграла. Этот раздел занимается изучением природы основных операций математического анализа. Одна из наиболее важных проблем, которая привела к развитию теории меры и интегрирования, возникла в связи с рядами Фурье. За сто или более лет до Лебега было известно, что тригонометрическим многочленом, дающим наилучшее среднеквадратичное приближение к данной функции, является ряд, порождаемый коэффициентами Фурье данной функции. Иначе говоря, при заданном k,

принимает минимальное значение, если коэффициенты определяются по формулам Фурье:

Однако поскольку определение интеграла было сформулировано в 19 в., вскоре стало ясно, что ряды из синусов и косинусов могут сходиться к функциям, настолько разрывным, что они не интегрируемы; и в этом случае понятие среднеквадратичной аппроксимации становится совершенно бессмысленным. Поэтому потребовалось новое определение интеграла, допускающего более широкий класс интегрируемых функций. В частности, хотелось по возможности расширить понятие предела последовательности интегрируемых функций, зная при этом, что предельная функция также будет интегрируема. (См. также РЯДЫ.)

Теория Лебега.

Предложенное в 19 в. определение интеграла в общих чертах сводилось к следующему. Разобьем интервал от a до b точками x_i, так, что a = x₀ < x₁ < x₂ <... < x_n = b. Пусть Y_i – наименьшая верхняя грань всех значений функции f(x) для x_i – 1 Ј x Ј x_i, а y_i – наибольшая нижняя грань всех таких значений. Образуем верхнюю и нижнюю суммы:

Если эти верхние и нижние суммы имеют общий предел для любой последовательности разбиений, когда расстояние между точками разбиения стремится к нулю, то функция f(x) называется интегрируемой, а этот общий предел – ее интегралом и обозначается

Если f(x) слишком разрывна, то Y_i и y_i остаются существенно различными для слишком многих интервалов, и тогда верхние и нижние суммы не стремятся к общему пределу. В определении Лебега эта трудность устраняется раз и навсегда тем, что разбивается не область определения функции, а область ее значений, т.е. если c Ј f(x) Ј d при a Ј x Ј b, то точки разбиения 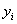выбираются таким образом, чтобы c = y₀ < y₁ < y₂ <... < y_n = d. Пусть E_i при каждом i будет множеством точек x, таких, что y_i – 1 Ј f(x) Ј y_i. В общем случае множество E_i будет не интервалом, а некоторым сложно устроенным множеством. Лебег усовершенствовал обобщение понятия длины таким образом, чтобы его можно было применять к множествам E_i в очень широком классе случаев. Эта обобщенная длина получила название меры множества E_i и стала обозначаться m(E_i). Верхняя и нижняя суммы Лебега имеют вид

Когда максимальная из разностей y_i – y_i – 1 стремится к нулю, эти суммы автоматически стремятся к общему пределу; следовательно f(x) – функция, интегрируемая в смысле Лебега, если только при любом разбиении области ее значений понятие меры применимо к возникающим множествам E_i. (См. также МНОЖЕСТВ ТЕОРИЯ.)

Множества, к которым применимо понятие меры, называются измеримыми, а функция, для которой любое разбиение области значений порождает разбиение ее области определения на измеримые множества, называется измеримой функцией. Одна из основных теорем в теории Лебега утверждает, что каждая ограниченная измеримая функция интегрируема на конечном интервале. С помощью подходящего предельного перехода интеграл в смысле Лебега распространяется на неограниченные функции и на бесконечные интервалы.

Определим меру Лебега. Пусть E – множество, принадлежащее интервалу от a до b. Последовательность интервалов I₁, I₂, I₃,ј, таких, что каждая точка из E принадлежит некоторым интервалам I_n, называется покрытием множества E. Для каждого покрытия множества E открытыми интервалами вычислим сумму их длин; наибольшая нижняя грань всех таких сумм называется «внешней мерой» множества E и обозначается m*(E). Внутренняя мера множества E обозначается m_*(E) и определяется как m_*(E) = b – a – m*C(E), где C(E) – множество всех точек, заключенных между a и b, не принадлежащих E. Множество E измеримо, если его внешняя и внутренняя меры равны; если это так, то m(E) – общее значение m*(E) и m_*(E).

Не все функции измеримы, но класс таких функций все же достаточно обширен, поскольку включает в себя все непрерывные функции, а также все поточечные пределы последовательностей измеримых функций. Последнее очень важно, так как если измеримость переносится на предельную функцию, то в этом случае она переносится и на интегрируемость, и появляется надежда решить проблему рядов Фурье.

Основные предельные теоремы.

Теория Лебега отвечает одной из основных потребностей, связанных с предельным переходом, – она обеспечивает сохранение интегрируемости при операции сходимости в среднем квадратичном; под этим понимается следующее: если f₁(x), f₂(x), f₃(x),... – последовательность функций, каждая из которых интегрируема по Лебегу (в смысле Лебега) на измеримом множестве E, и если

то на E существует интегрируемая функция f(x), такая, что

Аналогичная теорема существует и относительно сходимости в среднем квадратичном, т.е. о сходимости к нулю интеграла от [f_m(x) – f_n(x)]². Отсюда берет начало теорема Рисса – Фишера (1907), дающая ответ на вопрос относительно рядов Фурье, о котором говорилось в начале этой статьи. Именно, если ряд

сходится, то существует функция f(x), квадрат которой интегрируем в смысле Лебега, и такая, что

Значение теории Лебега состоит в том, что она требует выполнения весьма слабых условий для среднеквадратичной сходимости интеграла Лебега. Последовательность функций сходится по мере, если при любом заданном e > 0 мера множества, на котором |f_m(x) – f_n(x)| і e, стремится к нулю при m ® Ґ и n ® Ґ. Классическая теорема, также принадлежащая Лебегу, утверждает, что если последовательность измеримых функций f₁(x), f₂(x), f₃(x),... сходится по мере на измеримом множестве E и если существует интегрируемая функция g(x), такая, что |f_n(x)| Ј g(x) при всех n, то существует интегрируемая функция f(x), такая, что

Подводя итог, можно сказать, что сходимость по мере вместе с равномерным мажорированием интегрируемой функцией влечет за собой сходимость в среднем.

Со времен Лебега условие равномерного мажорирования удалось заменить более слабым условием. Предположим, что для каждой стягивающейся последовательности E₁, E₂, E₃, ... измеримых множеств из E, не имеющих ни одной общей для всех точки, равномерно по n выполняется соотношение

Тогда из сходимости по мере следует сходимость в среднем на E.

Аксиоматический подход.

Мера Лебега первоначально была определена для множеств на действительной прямой и привела к теории интегрирования по таким множествам. Применительно к более общим множествам ее основные положения и результаты приводят к абстрактной теории интегрирования, в свою очередь имеющей многочисленные реализации и приложения.

Исходным пунктом одной из таких абстрактных теорий стало аксиоматическое задание внешней меры, предложенное К.Каратеодори (1873–1950). Рассмотрим абстрактное пространство S. Предположим, что величина m*(A) определена для любого подмножества A из S. Эта функция множества m* называется «внешней мерой», если она удовлетворяет следующим условиям:

1) m*(f) = 0, если f – пустое множество;

2) m*(A) Ј m*(B), если A содержится в B;

3) 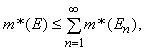если E₁, E₂, E₃,... – любая последовательность множеств, покрывающих множество E.

Внешняя мера Лебега (описанная выше) обладает этими свойствами, причем оказывается, что для нее эти свойства являются определяющими. Если задана любая m*, удовлетворяющая этим условиям, то измеримость множеств определяется утверждением, что E измеримо, если для любого множества A выполняется соотношение m*(A) = m*(A З E) + m*(A – E). Здесь A З E (пересечение A и E) означает множество точек, принадлежащих одновременно A и E; а A – E – множество точек, принадлежащих A, но не принадлежащих E. Интуитивно измеримое множество воспринимается как «хорошее», и определение Каратеодори говорит о том, что множество E измеримо, если не существует такого множества А, которое бы разделяло Е на две части, внутреннюю и внешнюю, так, что их внешние меры складываются «неправильно». Предложенное Лебегом определение измеримости, использующее внутреннюю меру, – частный случай условия Каратеодори, в котором A = S. Из-за некоторых специальных свойств внешней меры Лебега это условие оказывается достаточным для модели Лебега, но в общем случае требуется проверять измеримость более детально.

Ключевая теорема в теории Каратеодори утверждает, что любая внешняя мера, удовлетворяющая введенным аксиомам, при ограничении только на измеримые множества обладает всеми свойствами, которыми должна обладать мера. Самое важное из этих свойств называется полной аддитивностью. Мера m называется вполне аддитивной, если для любой последовательности E₁, E₂, E₃,... измеримых множеств, никакие два из которых не имеют общей точки,

(Символ в скобках в левой части равенства означает объединение множеств E_n, т.е. множество точек, принадлежащих по крайней мере одному из множеств E_n.)

Если дана любая вполне аддитивная мера, то затем можно, более или менее следуя Лебегу, определить интеграл, удовлетворяющий основным предельным теоремам, приведенным ранее в этой статье; следуя теории Каратеодори, можно для этих же целей исходить из внешней меры.

Построение внешних мер.

Существует совершенно стандартная процедура построения примеров внешних мер. Задача заключается в следующем: внешняя мера должна быть определена на всех множествах в пространстве, а простой формулы для таких функций обычно не существует. Приходится выбирать гораздо более узкий класс относительно простых множеств, задавать на них конкретную функцию и, пользуясь ею, порождать внешнюю меру. В большинстве случаев не удается представить наглядно ничего, кроме первоначальной функции на основном классе простых множеств; однако можно доказать, что такая функция действительно порождает внешнюю меру, а значит, и меру, и, следовательно, интеграл.

Метод построения внешних мер в точности повторяет тот, которым пользовался Лебег и который был описан в нашей статье выше. Суть его сводится к следующему. Пусть t – функция, определенная на некотором классе множеств. Если E₁, E₂, E₃,... – последовательность множеств, на которых определена t, и если эта последовательность множеств покрывает множество A, то образуем сумму

Тогда m*(A) – по определению наибольшая нижняя грань всех сумм, получаемых указанным способом.

В случае меры Лебега в качестве простых множеств используются открытые интервалы, и функция t, о которой говорилось выше, является длиной; т.е. выбрав для любого открытого интервала t в качестве t (I) его длину и проделав процедуру, описанную в предыдущем абзаце, мы получим внешнюю меру Лебега.

Более общая конструкция состоит в следующем. Минимальный набор требований сводится к тому, чтобы каждое множество можно было покрыть последовательностью множеств, на которых определена t, и чтобы сама функция t всюду была неотрицательна и обращалась в нуль на пустом множестве. Если эти условия выполняются для t, то можно доказать, что описанный метод порождает внешнюю меру. Но если на t наложены только перечисленные выше минимальные условия, то относительно получающейся внешней меры можно извлечь не слишком много информации. Например, нельзя с уверенностью утверждать, что базовые множества, на которых определена t, окажутся измеримыми, а также, что для такого множества t (E) = m*(E).

С другой стороны, если удостовериться, что t обладает более тонкой структурой, то относительно внешней меры появляется дополнительная информация. В различных вариантах абстрактной теории меры на функцию, используемую для построения внешней меры, накладываются различные условия. Обычно используются следующие. Предположим, что t определена на кольце множеств (семействе множеств, замкнутом относительно операций взятия разности и конечного объединения). Если t определена на кольце и вполне аддитивна, то множества в кольце оказываются измеримыми, а мера, которая при этом получается, обладает всеми свойствами функции t на кольце.

Дифференцирование.

Один из фундаментальных фактов математического анализа состоит в том, что дифференцирование и интегрирование – взаимно обратные процедуры. Возникает вопрос, переносится ли этот факт на рассматриваемые нами более общие теории интегрирования и дифференцирования. Кратко можно сказать, что для интеграла, построенного с помощью меры Лебега на действительной прямой, существует достаточно хорошая теория дифференцирования, но для любой более общей модели необходимы дополнительные уточнения. Важно отметить, что даже для интегралов, порожденных теорией плоской меры Лебега (меры, построенной по функции t, определяющей площадь прямоугольников на плоскости), теория дифференцирования становится более тонкой.

При обсуждении вопросов дифференцирования, связанных с теорией меры, существует формальное видоизменение обычного дифференцирования, основанное на том, что интегралы рассматриваются как функции множества, а не как функции точки. Таким образом, задача сводится к тому, чтобы одну функцию множества a, возможно, интеграл, продифференцировать по другой функции множества – мере m. Определение производной принимает форму

Не вдаваясь в детали, можно сказать, что I ® x означает здесь, что множество I стягивается в точку x. Основная трудность связана именно с точной интерпретацией этой идеи. Проверим ее разными способами.

Пусть f(x) – функция, интегрируемая по Лебегу на части действительной прямой, и пусть a(E) определена для каждого измеримого множества E из области определения функции f формулой

Определим теперь дифференцирование функции a следующим образом. Выберем в качестве множеств I замкнутые интервалы. Возьмем, далее, произвольные стягивающиеся последовательности этих интервалов, имеющих общей точкой лишь точку x, интерпретируя этот процесс как I ® x. При этих условиях можно доказать, что aў(x) существует и равна f(x) всюду, за исключением, может быть, тех точек множества, мера которых равна нулю. Математики используют в подобных случаях терминологический оборот, говоря, что «aў = f почти всюду». Нестрого можно утверждать, что «если имеется интегрируемая функция, то дифференцирование интеграла позволяет почти всюду восстановить подынтегральную функцию».

Но можно поступить и иначе. Ключевые свойства интеграла как функции множества заключаются в том, что он вполне аддитивен и абсолютно непрерывен, т.е. обращается в нуль на множествах меры нуль. Если m – мера Лебега на действительной прямой, дифференцирование определено относительно произвольной последовательности стягивающихся замкнутых интервалов, а функция a вполне аддитивна и абсолютно непрерывна, то aў существует почти всюду, и для каждого измеримого множества E

На плоскости ситуация сложнее. Чтобы доказать, что интеграл почти всюду дифференцируем и его производная равна подынтегральной функции, необходимо ограничить определение производной. Используя стягивающиеся в точку прямоугольники, необходимо наложить два ограничения: стороны прямоугольников всегда должны быть параллельны координатным осям, и при стягивании отношение длины и ширины должно оставаться неизменным или по крайней мере одного и того же порядка. При таких ограничениях интеграл почти всюду дифференцируем, производная его совпадает с подынтегральной функцией, но этот результат утрачивает силу, если допустить наклонные прямоугольники или когда отношение сторон меняется при стягивании прямоугольников в точку.

Если абсолютно непрерывная, вполне аддитивная функция задается на плоских множествах, то необходимо дополнительно потребовать, чтобы ее значение на любом измеримом множестве было сколь угодно точно аппроксимируемо ее значением на накрывающем открытом множестве. Тогда функция дифференцируема в ограниченном выше смысле почти всюду и равна интегралу от своей производной.

Если потребовать, чтобы длина и ширина прямоугольников, используемых в определении производной, были величинами одного и того же порядка, то можно воспользоваться теоремой, согласно которой интеграл почти всюду имеет производную, равную подынтегральной функции. Но все рушится, если отказаться от требования ограниченности. Утверждение теоремы становится неверным в топологическом смысле для большинства неограниченных подынтегральных функций.

Наконец, существует весьма абстрактная теорема Радона – Никодима (1930), согласно которой, если функция a определена на классе измеримых множеств и всюду конечна, вполне аддитивна и абсолютно непрерывна, то существует функция точки f, такая, что для каждого измеримого множества E функция a(E) является интегралом от f по E. Функцию f поэтому можно рассматривать как абстрактную производную от a, однако ни формулировка теоремы Радона – Никодима, ни ее доказательство не дают оснований для интерпретации этой абстрактной производной как предела отношения. Производная в данном случае определяется единственным способом – как решение некоторого интегрального уравнения. Иначе говоря, абстрактная производная от a есть функция f, такая, что для любого измеримого множества E

Интеграл Даниеля.

Другой подход к определению интеграла был предложен П.Даниелем в 1917. С тех пор и этот подход стал предметом многочисленных обобщений. Основная идея Даниеля состоит в формальном определении интеграла в терминах его свойств как функции подынтегрального выражения. Ключевыми являются такие свойства как линейность (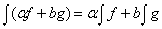), монотонность (если f Ј g, то 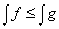) и непрерывность (если f ® g, в каком-то принятом смысле, то ).

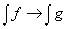Один из вариантов подхода Даниеля заключается в следующем. Рассмотрим ступенчатую функцию на некотором заданном интервале действительной оси. (Ступенчатой называется функция, постоянная на каждом из конечного множества интервалов, в силу чего ее график напоминает ступени лестницы.) Каждой ступенчатой функции f поставим в соответствие число I(f); потребуем, чтобы функция I была линейной, монотонной и непрерывной (предположим, что I(af + bg) = aI(f) + bI(g) для любых ступенчатых функций f и g и любых чисел a и b). Потребуем также, чтобы I(f) Ј I(g), если f Ј g, и чтобы I(f_n) ® I(f), если ступенчатые функции f_n монотонно стремятся к ступенчатой функции f. Пусть M – наименьший класс функций на выбранном интервале, содержащий все ступенчатые функции и замкнутый относительно операции взятия монотонных пределов. Назовем M – классом измеримых функций. Можно показать, что существует единственное расширение функции I с множеством ступенчатых функций на весь класс M, которое остается линейным, монотонным и непрерывным на M. Этот расширенный оператор, который переводит функцию в число, называется интегралом.

В подходе Даниеля интеграл рассматривается всего лишь как функция подынтегрального выражения, поэтому в результате мы получаем интеграл от f, но о том, по какому множеству проводится интегрирование, ничего не говорится. Если в теории Даниеля и приходится по чему-нибудь интегрировать, так это по всему базисному интервалу, и то, что в теории Лебега называлось бы интегралом от f по E, в теории Даниеля есть интеграл от f, умноженный на функцию, равную I на E и 0 вне E.

Интеграл Даниеля определяется без использования меры, однако с его помощью можно получить саму теорию меры. Различие состоит в том, что здесь мера выводится из интеграла, а не наоборот. Допустим, что некоторый класс измеримых функций и интеграл могут быть определены указанным выше образом. Множество E из базового интервала считается измеримым, если его характеристическая функция (функция, равная I на E и 0 вне E) принадлежит классу измеримых функций. Тогда меру множества E можно определить как интеграл от характеристической функции множества E. Таким образом, в подходе Даниеля возникает вся та теория, которая в другом порядке развертывается в подходе Лебега.

Наконец, следует отметить, что на множестве ступенчатых функций может быть задано много различных линейных, монотонных, непрерывных функционалов, каждый из которых приводит к другому понятию интеграла и последующему понятию меры. Но если за I(f) принять площадь под графиком функции f, то подход Даниеля просто воспроизводит интеграл Лебега и меру Лебега.

ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

Под «функциями комплексного переменного» обычно принято понимать аналитические (или голоморфные) функции, особый класс функций, представимых степенными рядами. По традиции этот предмет был и в определенной степени продолжает оставаться в самом центре математического анализа; и хотя теория функций комплексного переменного необычайно важна как активно развивающаяся область чистой математики, своим существованием и в значительной мере своим высоким престижем теория функций комплексного переменного обязана успехам в решении проблем прикладной математики в таких областях, как теория дифференциальных уравнений, гидродинамика и теория потенциала. Известная ранее под общим названием «теория функций», эта теория обрела независимое существование в конце 19 в., когда под давлением более строгого истолкования понятий множества, числа, интеграла и производной произошло разделение между теорией функций действительного переменного и теорией функций комплексного переменного.

КЛАССИЧЕСКАЯ ТЕОРИЯ

Богатство и разнообразие теории функций комплексного переменного обусловлено взаимодействием геометрии и анализа. Когда речь заходит о комплексном числе z = x + iy (где i² = –1), мы можем представить его как число, удовлетворяющее правилам алгебры или как точку на декартовой (или комплексной) плоскости с координатами x и y. Производя операции над комплексными числами, мы можем использовать либо алгебраические методы, либо геометрические, либо комбинацию того и другого. Абсолютной величиной или модулем комплексного числа называется положительное действительное число 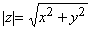, или расстояние от z до начала координат. Этот двойственный аспект был отмечен и использован К.Гауссом (1777–1855) и Х.Гамильтоном (1805–1865).

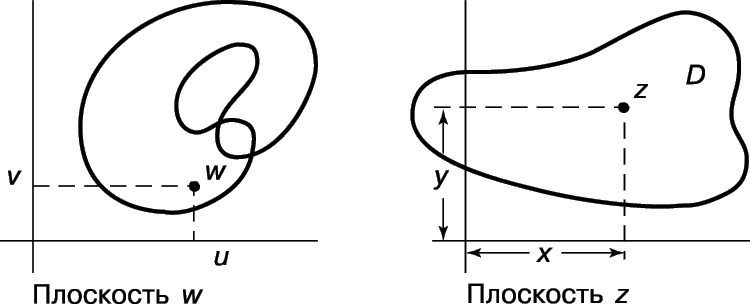
Но основной интерес здесь для нас представляют не комплексные числа сами по себе, а комплексные функции. Комплексная функция F, областью определения которой служит множество D комплексной плоскости Z ставит в соответствие каждой точке z из D, вообще говоря, другое комплексное число F(z). Чтобы получить геометрическую интерпретацию такой функции, возьмем вторую комплексную плоскость с точками w = u + iv и отметим точки w = F(z). В результате мы получим новое множество точек (некоторые из которых могут возникать от различных значений z). Новую плоскость w часто считают результатом отображения или преобразования области D (см. рис. 5). Действительную и мнимую части функции F(z) представляют две действительные функции f и y, которые можно рассматривать либо как действительные функции переменной z, либо как действительные функции переменных x и y:

Например, если каждому z мы ставим в соответствие комплексное число w = F(z) = z², полагая w = u + iv и z = x + iy, выделив отдельно действительную и мнимую части, то получим:

С другой стороны, если F(z) = 2z + 3iERROR, где ERROR означает комплексное число x – iy, сопряженное с z, получаем:

Важный класс комплексных функций состоит из полиномиальных функций или многочленов P. Если C₀, C₁,..., C_n – комплексные числа, то многочлен P определяется как

Простым примером многочленов может служить w = z². Точно также, как мы представили в действительном виде эту простую полиномиальную функцию, мы можем представить и многочлен (4), записав каждый коэффициент c_k в виде a_k + ib_k и произведя умножение. Однако, хотя на первый взгляд отображение (3) имеет более простую структуру, можно показать, что его нельзя записать в виде многочлена.

Такое различие в структуре стало основанием для выделения особого класса функций комплексного переменного, которые получили название аналитических (иногда их также называют голоморфными или моногенными). Идея заключалась в том, чтобы выделить те функции, которые представимы с помощью формул, содержащих z, а не x и y в отдельности (такие функции можно было бы «анализировать» как функции непосредственно от z) аналогично тому, как содержат z многочлены. Класс аналитических функций выбран так, чтобы он содержал все рациональные функции R(z) = P(z)/Q(z), где P и Q – многочлены типа (4); о таких функциях говорят, что они аналитичны на всей плоскости, кроме точек z, в которых Q(z) = 0, так как в этих точках R(z) не определена. Например, функция w = (z² – 1)/(z² + 1) аналитична на всей плоскости, за исключением точек i и -i. Самыми общими аналитическими функциями являются функции, которые получаются взятием соответствующих пределов от рациональных функций. В частности, следуя подходу, предложенному гораздо позднее К.Рунге (1856–1927), функция F(z), определенная в области D, называется аналитической, если можно выбрать подмножество D₀, принадлежащее D, и, задав сколь угодно малую допустимую погрешность e > 0, найти некоторую рациональную функцию R(z), аппроксимирующую функцию F(z) на D₀, так, чтобы |F(z) – R(z)| никогда не превышало e при любом z из D₀.

Более традиционный подход к аналитическим функциям основан на понятии производной. Из математического анализа берется элементарное определение производной и ставится вопрос, может ли функция F иметь комплексную производную Fў, задаваемую такой же формулой, как в анализе, т.е.

Предельный переход здесь понимается применительно к плоскости: говорят, что 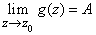существует, если все значения g(z) лежат вблизи A, когда z принадлежит достаточно малой окрестности точки z₀. Математикам начала 18 в. было ясно, что такое дифференцирование осуществимо для многих конкретных функций F, в том числе для многочленов P, задаваемых формулой (4). В этом случае

что полностью согласуется с правилами элементарного математического анализа.

Естественно, что класс всех функций F, для которых возможно дифференцирование, оказался под пристальным вниманием; эти функции получили название моногенных, впоследствии – аналитических функций. Требование дифференцируемости может быть переведено на язык ограничений на действительные функции f и y, составляющие функцию F. Если F(z) = w = u + iv = f(x,y) + iy (x,y), то можно вычислить четыре первые частные производные от f и y, обозначив их fx, fy, yx, yy или

Расположим эти четыре функции в виде таблицы или матрицы размером 2ґ2:

Можно показать, что из существования производной (5) следует, что матрица (6) должна иметь вид

Соответственно, действительная и мнимая части функции F должны удовлетворять так называемым дифференциальным уравнениям Коши – Римана:

Смысл этих соотношений можно лучше понять, если иметь ввиду, что матрица (6) в данном случае представляет то, что в современном математическом анализе принято называть дифференциалом отображения F и что матрицы вида (7) образуют поле, изоморфное полю комплексных чисел.

Возвращаясь к иллюстративным примерам (2) и (3), мы видим, что соответствующие матрицы имеют вид

Таким образом, мы заключаем, что функция (2) аналитическая, а функция (3) – не аналитическая.

Аналитические функции, более общие, чем многочлены, легко строятся с помощью бесконечных рядов; если |c_n| Ј RⁿA при n = 0, 1,..., то ряд

сходится в открытом «диске» (области, заключенной внутри окружности) радиуса R с центром в точке b и в этом диске определяет аналитическую функцию. С помощью бесконечного ряда можно определить, например, экспоненциальную и тригонометрические функции

каждая из которых аналитична для любых значениях z на плоскости. Используя операции с бесконечными рядами, можно также вывести тождества

Таким образом, комплексные экспоненциальная и тригонометрические функции удовлетворяют тем же тождествам, что и соответствующие действительные функции в математическом анализе и тригонометрии. Если действительное число e определено как значение экспоненциальной функции

то exp(z) можно принять за определение функции e как для действительных, так и для комплексных z. Из формулы (11) следует, что 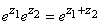. В сочетании с надлежащим определением логарифмической функции это позволяет дать вполне приемлемое определение величины a^b для произвольных действительных или комплексных чисел a и b, a № 0.

Большая заслуга в развитии этой области математики принадлежит О.Коши (1789–1857), систематизировавшему массу результатов, которые ранее некритически и формально трактовались в работах Л.Эйлера (1707–1783) и других математиков, и создавшему на этой основе последовательную и удивительно красивую теорию. Однако следующие поколения математиков обнаружили, что многие доказательства Коши неполны. Современную форму теория функций комплексного переменного обрела в работах Б.Римана (1826–1866), К.Вейерштрасса (1815–1897) и других математиков. Основным итогом их усилий явилось доказательство полного совпадения класса аналитических функций с классом функций, представимых «локально» (т.е. в окрестности каждой точки) сходящимся степенным рядом. Коэффициенты этого ряда имеют вид c_n = f ⁽ⁿ⁾(z₀)/n!, а ряд с такими коэффициентами известен в математическом анализе как ряд Тейлора. Доказательство этой эквивалентности, как и многих других важных свойств аналитических функций, опирается на замечательное открытие Коши и Д.Мореры (1856–1909), показавших, что аналитические функции можно задавать не только с помощью производных, но и интегралов; аналитическими являются те непрерывные функции f, для которых интеграл по контуру g на комплексной плоскости

всегда равен нулю для любой достаточно малой простой замкнутой кривой g, лежащей в области D. Причина этого заключена в уравнениях Коши – Римана (8) и в формуле для действительных интегралов, получившей название теоремы Грина в честь Дж.Грина (1792–1841). Пусть D₀ – часть области D, ограниченная контуром g. Тогда теорема Грина утверждает, что для произвольных функций A(x, y) и B(x, y)

Применяя ее к двум действительным интегралам, на которые распадается 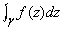, получаем

и, следовательно,

Этот результат, названный интегральной теоремой Коши, позволяет, в свою очередь, получить интегральную формулу Коши

дающую выражение для дифференцируемой функции во внутренних точках замкнутого контура через значения функции на самом контуре.

Из формулы (12) следует удивительный вывод: если функция f аналитична в области D, то она не только имеет производную f ў, определенную в каждой точке области D, но и эта новая функция f ў также аналитична в D. Продолжая по индукции, мы заключаем, что аналитическая функция обладает производными всех порядков, каждая из которых аналитична. В этом – существенное различие между теориями функций действительного и комплексного переменного: в теории функций действительного переменного функция g может иметь производную g ў(x), определенную для всех действительных чисел x, но производная g ў(x) может не быть дифференцируемой и даже непрерывной. (Такова, например, g(x) = x²sin(1/x).)

СОВРЕМЕННАЯ ТЕОРИЯ

Пользуясь в основном такими средствами, как степенные ряды, контурный интеграл и дифференцирование, математики в последующие десятилетия сумели достичь значительных успехов в изучении следствий из предположения об аналитичности функций. Перечень имен тех, чьи труды способствовали прогрессу в этой области, простирается от П.Дирихле (1805–1859) и Римана и до Г.Вейля (1885–1955), У.Осгуда (1864–1943), Ж.Валирона (1885–1955), Г.Шварца (1843–1921), Р.Неванлинны (1895–1980) и других аналитиков, ныне активно работающих в теории функций и смежных областях.

Многие удивительные свойства аналитических функций легко представить на языке геометрии или топологии. Начнем с того, что откажемся от точки зрения, которой мы до сих пор руководствовались и согласно которой функция задается аналитической формулой, например, бесконечным рядом. Вместо этого будем рассматривать функцию F как отображение z ® w = F(z), ставящее в соответствие точкам плоскости z точки плоскости w. Если S – любое множество точек из области определения функции F на плоскости z, то F(S) – образ этого множества на плоскости w, состоящий из всех точек F(z), таких, что z принадлежит S. Множество S называется открытым, если каждая точка множества S является центром диска, целиком лежащего в S. Одно из важных свойств аналитической функции F состоит в том, что образ любого открытого множества S на плоскости z всегда является открытым множеством на плоскости w, если только F – не константа. Из этого топологического свойства можно вывести знаменитый «принцип максимума модуля»: если функция f аналитична и не является константой в замкнутой области D, то наибольшее значение действительной непрерывной функции |f(z)| достигается, когда z – не внутренняя точка области D, а лежит на границе области D.

В топологии гомеоморфизмом называется взаимно однозначное непрерывное отображение, которое переводит открытые множества в открытые; аналитические функции обычно гомеоморфизмами не являются. Например, отображение z ® e^z, задаваемое экспоненциальной функцией, не взаимно однозначно, а отображает каждую из точек z₀ + 2kpi в одну и ту же точку плоскости w при k = 0, ±1, ±2,...; но эти точки расположены так далеко одна от другой, что отображение, задаваемое экспоненциальной функцией, взаимно однозначно (и, следовательно, гомеоморфно) на любой круговой области плоскости z, диаметр которой меньше 2p. Такое поведение описывают, говоря, что отображение z ® e^z «локально» гомеоморфно на всей плоскости z. Аналогично обстоит дело и в общем случае. Можно показать, что если функция F аналитична на множестве D и мы удалим из D все точки, в которых Fў принимает нулевое значение, то на остальной части множества D функция F задает локальный гомеоморфизм. Например, w = z² + 1 определяет локальный гомеоморфизм на всей плоскости z за исключением начала координат.

Отсюда следует еще одно особое свойство. Если функция F аналитична в области D и отлична от константы, то можно попытаться определить множество S точек z из D, которые служат решениями уравнения F(z) = A. Разумеется, таких точек может не быть; однако можно показать, что если таких точек бесконечно много, то они должны сходиться к границе области D. Удивительным следствием этого факта является теорема единственности для аналитических функций, отражающая гибкую природу аналитической функции: если f и g – функции, каждая из которых аналитична в одной и той же области D, и если значения функций f и g совпадают на множестве S, содержащем малый диск или малую дугу, или даже на сходящейся последовательности точек из D, то f и g совпадают на всей области D. Это свойство иногда называют перманентностью формы: если известно, что формула (10) выполняется для действительных чисел t, 0 < t < p, то мы можем сразу же заключить, что она должна выполняться и для всех комплексных значений t.

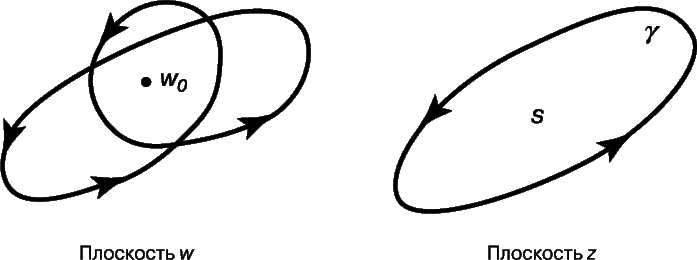
Как уже упоминалось, аналитические функции отображают открытые множества в открытые. Естественно задать вопрос: если D₁ – открытая область на плоскости z, а D₂ – открытая область на плоскости w, то существует ли функция f, аналитическая на D₁, которая отображает, причем взаимно однозначно, D₁ на D₂? Если ответ на этот вопрос утвердительный, то говорят, что f конформно отображает D₁ на D₂, а об областях D₁ и D₂ говорят, что они принадлежат к одному и тому же конформному типу. В качестве примера заметим, что вся плоскость и любой открытый диск принадлежат к различным конформным типам; это следует из теоремы Ж.Лиувилля (1809–1882), которая гласит: любая функция F, аналитическая на всей плоскости, не может отображать плоскость на любое ограниченное множество (лежащее целиком внутри какого-нибудь диска конечного радиуса), если только F не константа. Наиболее известный результат такого рода – теорема Римана об отображениях, которая утверждает, что любая односвязная открытая область D на плоскости принадлежит к тому же конформному типу, что и открытый круговой диск единичного радиуса. (Под односвязностью здесь имеется в виду топологическое понятие, означающее в данном случае, что плоскость не распадается на два или большее число кусков, если из нее удалить область D.)

Вопрос о конформном типе многосвязной области (рис. 6) более сложен. Две области с одним и тем же числом дырок необязательно принадлежат одному и тому же конформному типу, хотя они и гомеоморфны. Например, любая двусвязная область принадлежит тому же конформному типу, что и некоторое кольцо (рис. 6) с внутренним радиусом, равным 1; однако два таких кольца конформно неэквивалентны за исключением того случая, когда их размеры в точности совпадают.

Полезно также рассмотреть, каким образом аналитическая функция отображает кривые на плоскости z на кривые на плоскости w. Если a и b – две гладкие кривые, проходящие через точку z₀, образуя в этой точке между собой угол q, то их образам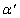и и 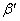будут кривые, проходящие через точку w₀ = F(z₀) и образующие в этой точке между собой некоторый угол (рис. 7). Из уравнений Коши – Римана (7) следует, что всегда 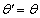за исключением того случая, когда Fў(z₀) = 0. Но и в последнем случае кое-что можно утверждать, не ограничивая общности, так как 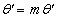, где m – наименьшее из целых чисел k, при которых F^(k)(z₀) № 0. Поэтому говорят, что в общем случае аналитические функции задают конформные (т.е. сохраняющие углы) отображения; например, w = z² + 1 – отображение, конформное всюду за исключением начала координат, где углы удваиваются.

Исследуя, каким образом аналитическая функция отображает кривые, можно получить также дополнительную информацию и о ней самой. Пусть g – замкнутая кривая, лежащая в односвязной области D, в которой функция f аналитична; предположим, что g не имеет самопересечений. Пусть S – область, границей которой служит g. Образ g ў кривой g под действием отображения f может пересекать самого себя несколько раз (рис. 8). Выберем любую точку w₀, не лежащую на кривой g ў, и подсчитаем сколько раз g ў делает полный обход вокруг w₀ (число обходов обозначим N). (На рис. 8 N = 2.) Тогда в области S должно быть ровно N решений уравнения f(z) = w₀. Это утверждение, известное под названием «принцип аргумента», является основным инструментом анализа расположения нулей (точек, в которых w₀ = 0) аналитической функции.

Исследование природы аналитических функций продолжает привлекать внимание многих математиков. Хотя трудно перечислить их достижения, не вдаваясь при этом в излишне специальные детали, нельзя не упомянуть некоторые из направлений современных исследований. Среди общих целей – (1) установление взаимосвязей между распределением нулей аналитической функции и способом, которым она отображает некоторое семейство областей (например, дисков); (2) изучение поведения аналитической функции вблизи границы ее области определения; (3) установление зависимостей между поведением функции в одной точке и ее поведением в какой-то другой точке, находящейся на некотором расстоянии от первой и (4) установление характеристических свойств, которыми обладают все функции некоторого класса (например, свойство всех функций f отображать данную область D₁ на область D₂). В последнее десятилетие математики стали уделять больше внимания сложным проблемам, связанным с теорией функций двух и более комплексных переменных, аналитических по каждой из переменных в отдельности.

ПРИЛОЖЕНИЯ

В естественных науках.

Аналитические функции широко используются в некоторых областях науки и техники просто потому, что дают в руки исследователя удобный математический аппарат. Ч.Штейнметц (1865–1923) был первым, кто привлек внимание инженеров-электриков к тем практическим преимуществам, которые дают комплексные функции при рассмотрении проблем, связанных с переменным током. Аналогично, для упрощения процедуры решения линейных дифференциальных уравнений, возникающих в электротехнике и механике, О.Хевисайд (1850–1925) ввел формальное операционное исчисление, которое ныне вытеснено преобразованиями Лапласа и Фурье, представляющих частные случаи интегрального представления Коши из теории аналитических функций. В связи с этим при вычислении несобственных действительных интегралов, часто возникающих в практических проблемах, широко используется теория вычетов Коши.

Более основательный вклад был внесен теорией аналитических функций в гидродинамику и теорию теплопроводности. Первая точка соприкосновения – связь с понятием гармонической функции. Если функция F аналитична в области D и F(z) = u + iv, то дифференцируя уравнения Коши – Римана (7), нетрудно убедиться в том, что u и v – решения дифференциального уравнения Лапласа в частных производных

Любое решение уравнения (13) в области D называется функцией, гармонической в D. Таким образом, действительная (или мнимая) часть любой аналитической функции – функция, гармоническая всюду. Наоборот, если H – любая функция, гармоническая в односвязной области D, то она является действительной частью некоторой комплексной функции F, аналитичной в D.

Дифференциальное уравнение типа (13) возникает во многих задачах в различных областях науки и техники. Оно является математической формулировкой закона о распределении температуры в неравномерно нагретом теле. Левая часть этого уравнения входит в так называемое волновое уравнение, играющее фундаментальную роль в теории колебаний. Неудивительно, что прикладные математики широко используют методы теории функций комплексного переменного для решения своих задач.

В гидродинамике теория функций комплексного переменного используется для решения задач, связанных со установившимся плоско-параллельным течением несжимаемой безвихревой жидкости. Вектор скорости такой жидкости в точке (x, y) можно записать в виде a(x,y) + ib(x,y); в силу природы течения существует гармоническая функция u, такая, что

Функция u называется потенциалом скоростей течения. Соответствующая аналитическая функция F называется комплексным потенциалом скоростей, ее действительная часть совпадает с u. Пользуясь конформными отображениями, такую функцию можно использовать для описания линий тока при обтекании сложного профиля, погруженного в движущуюся жидкость. В аэродинамике изучение обтекания привело к открытию закона образования подъемной силы крыла самолета.

В чистой математике.

Математика – не коллекция изолированных друг от друга областей. Известные доказательства возможности разложения на n множителей любого многочлена P(x) = c₀ + c₁x +... + c_nxⁿ основано на использовании основных идей из теории функций, в частности теоремы Лиувилля или принципа аргумента (Гаусс, 1799). Доказательство теоремы о простых числах и ее уточнения, касающиеся частоты, с которой простые числа 2, 3, 5, 7, 11, ... встречаются среди целых чисел, основана на аналитической структуре некоторых комплексных функций, введенных Риманом, Дирихле и Ж.Адамаром (1865–1963). Необходимость уточнения некоторых интуитивно очевидных свойств плоских кривых на основе интегральной теоремы Коши, привело к появлению таких топологических понятий, как гомология и гомотопия (А.Пуанкаре, 1854–1912). Позднее изучение взаимосвязи между гармоническими функциями и аналитическими функциями, определенными на многосвязных множествах, привели к созданию понятия накрывающей поверхности и к более ясному пониманию понятия римановой поверхности, первоначально введенном (в 1851) для облегчения построения теории многозначных функций. В свою очередь это послужило стимулом к разработке таких идей в теории комплексных многообразий и общей теории пучков.