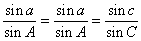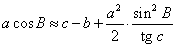СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ
СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ – математическая дисциплина, изучающая зависимости между углами и сторонами сферических треугольников.
Тригонометрия («измерение треугольников» по-гречески) началась именно с этой, наиболее сложной ее части. Различные случаи решения сферических треугольников были впервые письменно изложены греческим астрономом Гиппархом из Никеи в середине 2 в. до н.э., к сожалению, сочинение Гиппарха до нас не дошло. Свойства прямоугольных сферических треугольников были известны еще Менелаю (1 в.) и Клавдию Птолемею (ок. 90 – ок. 160) – создателю геоцентрической системы мира, господствовавшей до Коперника. В Альмагесте (Великом собрании) Птолемея (ок. 150) содержатся и многие сведения из трудов Гиппарха. В 10 в. багдадский ученый Мухаммед из Буджана, известный под именем Абу-ль-Вефа сформулировал теорему синусов. Насир-эд-Дин из Туса (1201–1274) систематически рассмотрел все случаи решения косоугольных сферических треугольников и указал ряд новых способов решения. В 12 в. был переведен с арабского на латынь ряд астрономических работ, что позволило ознакомиться с ними европейцам. Но, к сожалению, многое осталось непереведенным, и выдающийся немецкий астроном и математик Иоганн Мюллер (1436–1476), которого современники знали под именем Региомонтана (именно так переводится на латынь название его родного города Кенигсберга), через 200 лет после Насир-эд-Дина заново открыл его теоремы. Большой вклад в развитие сферической тригонометрии внесли так же Франсуа Виет (1540–1603) и Леонард Эйлер (1707–1783). До Эйлера теоремы формулировались исключительно геометрически – именно Эйлер (1753 и 1779) дал всю систему формул сферической тригонометрии.
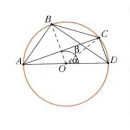
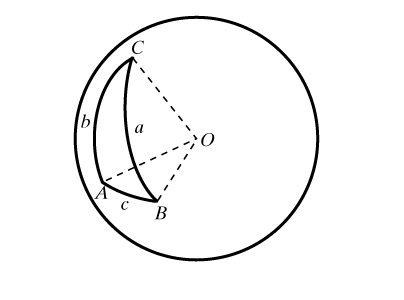
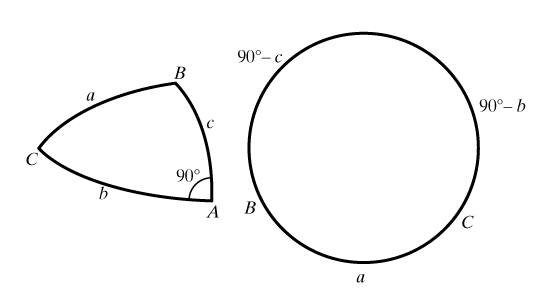
Пусть А, В и С – углы, а a, b и c – противолежащие им стороны сферического треугольника АВС (рис. 1). По любым трем элементам можно определить три остальные (в отличие от «плоской» геометрии, где три угла не определяют треугольник). Следующие формулы сферической тригонометрии связывают углы и стороны треугольника (т.е. позволяют решить треугольник):
sin a cos B = cos b sin c – sin b sin c cos A,
sin A cos b = cos B sin C – sin B sin C cos a,
sin a ctg B = sin C ctg b – cos c cos A;
в этих формулах стороны a, b, c измеряются соответствующими центральными углами, длины этих сторон равны соответственно aR, bR, cR, где R – радиус сферы. Меняя значения углов и сторон по правилу круговой перестановки: А ® B ® C ® А (а ® b ® c ® а), можно написать другие формулы сферической тригонометрии, аналогичные указанным.
Для прямоугольных сферических треугольников (А = 90°, а – гипотенуза, b и с – катеты) формулы сферической тригонометрии упрощаются:
sin b = sin а sin B,
cos а = cos b cos c,
sin а cos B = cos b sin c.
Для получения формул, связывающих элементы прямоугольного сферического треугольника, можно пользоваться следующим мнемоническим правилом (правилом Непера): если заменить катеты прямоугольного сферического треугольника их дополнениями до 90, не принимать во внимание прямой угол А и расположить остальные пять элементов по кругу (рис. 2) в том порядке, в каком они находятся в треугольнике, т.е. B, a, C, 90° – b, 90° – c, то косинус каждого элемента будет равен произведению котангенсов прилежащих или произведению синусов неприлежащих элементов. Например, cos B = ctg (90° – c)ctg a или cos B = tg c ctg a после преобразования; cos а = sin (90° – c) sin (90° – b) или cos а = cos b cos c.
При решении задач удобны следующие формулы Даламбера, связывающие все шесть элементов сферического треугольника:
sin ½ a cos ½ (B – C) = sin ½ A sin ½ (b + c),
sin ½ a sin ½ (B – C) = cos ½ A sin ½ (b – c),
cos ½ a cos ½ (B + C) = sin ½ A cos ½ (b + c),
cos ½ a sin ½ (B + C) = cos ½ A cos ½ (b – c);
из этих формул легко получаются неперовы аналогии.
При решении задач в зависимости от требуемой точности часто оказывается достаточным использование приближенных формул:
1) для малых сферических треугольников (т.е. стороны которых малы по сравнению с радиусом сферы) можно пользоваться формулами плоской тригонометрии;
2) для узких сферических треугольников (т.е. таких, у которых одна сторона, например, a, мала по сравнению с другими) применяют следующие формулы:
A » a sin B/sin c,
a cos B » c – b
или более точные формулы:
Формулы сферической тригонометрии находят широкое применение в сферической астрономии. Без этих формул невозможно обойтись, поскольку все измерения, связанные с расположением светил на небосводе – измерения косвенные. И долгое время сферическая тригонометрия считалась просто разделом астрономии.
Марина Федосова
Стройк Д.Я. Краткий очерк истории математики, Москва, «Наука», 1984
Ответь на вопросы викторины «Математика»