КООРДИНАТЫ

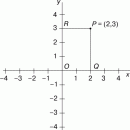
КООРДИНАТЫ, величины, при помощи которых в аналитической геометрии определяется положение точек, прямых и плоскостей. Наиболее распространенные — это координаты точки, введенные Ферма и Декартом, хотя в принципе известные еще Архимеду и Аполлонию. Положение точки на плоскости в этой координатной системе определяется расстояниями x и y от двух постоянных прямых ОХ и ОУ,  называемых координатными осями, причем расстояния эти отсчитываются параллельно осям и считаются положительными в одном направлении и отрицательными в противоположном. Ось ОХ называется осью абсцисс, и, ей параллельное, расстояние х точки Р от другой оси — абсциссою; вторая ось ОУ называется осью ординат и, параллельное ей расстояние у — ординатою. Точка пересечения координатных осей называется началом координат.

В пространстве берутся три,  взаимно пересекающиеся в одной точке, плоскости, взаимные пересечения которых называются координатными осями. Координаты какой-либо точки в пространстве будут параллельные осям расстояния точки от координатных плоскостей. В простейшем случае углы между координатными осями суть прямые; такая система координат наиболее употребительна и называется прямоугольной.

Почти такое же значение имеют полярные координаты, при которых положение точки Р на плоскости определяется расстоянием r = OP (радиусом-вектором) этой точки от начала координат (полюса) и углом φ, на который нужно повернуть положительную часть оси, чтобы совместить ее с точкой Р. В пространстве r или OP рассматриваются как радиус шара, центр которого О и на котором лежит точка Р; положение Р на шаре определяется долготою (λ) и широтою (β), введенными еще Гиппархом (150 до н.э.);  r , λ и φ называются сферическими координатами.

Если широта φ, т.е. угловое расстояние точки от основной плоскости, заменим линейным расстоянием от той же плоскости, то получим систему координат, называемую цилиндрической. 

На плоскости иногда определяют положение какой-либо точки ее расстояниями от двух постоянных точек. Такая система координат называется биполярной.

Со времени Мебиуса и Плюкера в координатной геометрии все более и более употребляются линейные однородные координаты, для чего при рассмотрении точек на плоскости вводятся расстояния этих точек от трех сторон треугольника, при рассмотрении же точек в пространстве — от четырех сторон тетраэдра, или, вернее сказать, не расстояния этих точек, а отношения этих расстояний. Линейные координаты впервые были введены Мебиусом в 1827 в его барицентрическом исчислении. Так как какие-либо три поверхности φ₁ (х, у, z) = p₁,  φ₂ (x, y, z) = p₂ и  φ₃ (x₁, y₁, z₁) = p₃ своим пересечением определяют некоторую точку, то можно рассматривать р₁, р₂ и р₃ как координаты точек. Такие координаты называются криволинейными. Если нормали в каждой точке пересечения поверхностей  φ₁, φ₂ и φ₃ взаимно перпендикулярны, то система называется ортогональной.

Криволинейные координаты впервые были введены Гауссом в учении о поверхностях, их теорию специально разрабатывал Ламе в сочинении Leçons sur les coordonnées curvilignes (Париж, 1859). Упомянутые выше полярные, сферические и цилиндрические координаты представляют собой соединение прямолинейных и криволинейных координатов.

Астрономические координаты всегда ортогональны и называются, смотря по тому, где помещено их начало, в центре ли Земли, Солнца, Луны или планет, геоцентрическими, гелиоцентрическими, селеноцентрическими или планетоцентрическими (например, ураноцентрические координаты). Если за основную плоскость принимается эклиптика, или экватор, или горизонт, то координаты, соответственно называются эклиптикальными, экваториальными или горизонтальными.

В большинстве случаев одна из координат, а именно радиус-вектор, неизвестна и две другие координаты определяют лишь направление этого радиуса-вектора. За вторую основную плоскость в эклиптикальных координатах принимают плоскость, перпендикулярную к эклиптике и проходящую через точку весеннего равноденствия ν; в экваториальных — или плоскость, проходящую через ν и перпендикулярную экватору или же меридиан; в горизонтальных — меридиан.

Положение светила определяется: 1. в эклиптикальных координатах — широтою, т.е. наименьшим угловым расстоянием от эклиптики, и долготою — т.е. Угловым расстоянием по эклиптике от  ν,  считая по направлению от запада к востоку; 2. в экваториальных координатах — склонением, т.е. наименьшим угловым расстоянием от экватора и прямым восхождением, т.е. угловым расстоянием от  ν, от запада к востоку или же часовым углом, т.е угловым расстоянием по экватору от востока к западу; 3. в горизонтальных — высотою, т.е. наименьшим угловым расстояние от горизонта и азимутом, т.е. угловым расстоянием по горизонту, считая от южной части меридиана по направлению к западу.

Географические координаты — широта, долгота и высота над уровнем моря. Широта есть расстояние по меридиану от экватора, причем к северу от экватора широты называются северными, к югу — южными. Долготы считаются по экватору от нулевого (первого) меридиана, который проводится через Гринвичскую обсерваторию (Великобритания), и к западу, и к востоку.