ЦИКЛОИДА

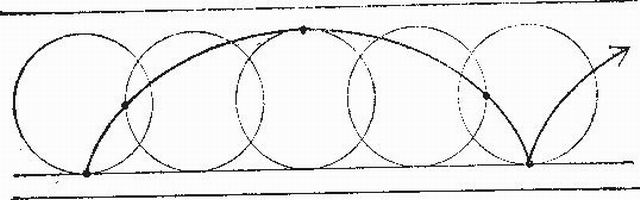
ЦИКЛОИДА (в переводе с греч. кругообразный) – плоская трансцендентная кривая, которую описывает точка окружности радиуса r, катящейся по прямой без скольжения (трансцендентной кривой называется кривая, которая в прямоугольных координатах не может быть описана алгебраическим уравнением). Ее параметрическое уравнение

x = rt – r sin t,
y = r – r cos t

Точки пересечения циклоиды с прямой, по которой катится окружность (эта окружность называется производящей, а прямая, по которой она катится, – направляющей), называются точками возврата, а самые высокие точки на циклоиде, расположенные посредине между соседними точками возврата, называются вершинами циклоиды.

Первым изучать циклоиду начал Галилео Галилей. Длина одной арки циклоиды была определена в 1658 английским архитектором и математиком Кристофером Реном, автором проекта и строителем купола собора Святого Павла в Лондоне. Оказалось, что длина циклоиды равна 8-ми радиусам производящей окружности.
Одно из замечательных свойств циклоиды, давшее ей название – брахистохрона (от греческих слов «кратчайший» и «время) связано с решением задачи о наискорейшем спуске. Встал вопрос, какую форму надо придать хорошо отшлифованному (чтобы практически исключить трение) желобу, соединяющему две  точки, чтобы шарик скатился вниз от одной точки к другой в кратчайшее время. Братья Бернулли доказали, что желоб должен иметь форму опрокинутой вниз циклоиды.

Родственные циклоиде кривые можно получить, рассматривая траектории точек, не находящихся на производящей окружности.

Пусть точка С₀ находится внутри окружности. Если провести через С₀ вспомогательную окружность с тем же центром, что и у производящей окружности, то при качении производящей окружности по прямой АВ маленькая окружность будет катиться по прямой A´В´, но ее качение  будет сопровождаться скольжением, и точка С₀ описывает кривую, называемую укороченной циклоидой.

Аналогичным образом определяется удлиненная циклоида – это траектория точки, расположенной на продолжении радиуса производящей окружности, при этом качение сопровождается скольжением в противоположном направлении.

Циклоидальные кривые применяются при многих технических расчетах и свойства их используются, например, при построении профилей зубьев шестерен, в циклоидальных маятниках, в оптике и, таким образом, изучение этих кривых важно с прикладной точки зрения. Не менее важно и то, что, изучая эти кривые и их свойства, ученые 17 в. разрабатывали приемы, которые привели к созданию дифференциального и интегрального исчислений, а задача о брахистохроне явилась шагом к изобретению вариационного исчисления. 

Елена Малишевская