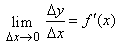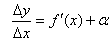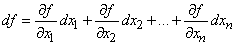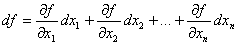ДИФФЕРЕНЦИАЛ

Содержание статьи

• Дифференциалы различных порядков.

ДИФФЕРЕНЦИАЛ – линейная часть приращения функции. Пусть функция y = f(x) дифференцируема на отрезке [a,b]. Производная этой функции в некоторой точке x отрезка [a,b] определяется равенством

.

ДИФФЕРЕНЦИАЛ – линейная часть приращения функции. Пусть функция y = f(x) дифференцируема на отрезке [a,b]. Производная этой функции в некоторой точке x отрезка [a,b] определяется равенством

.

Отношение 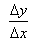стремится к определенному числу f ў(x) и, следовательно, отличается от производной f ў(x) на величину бесконечно малую:

,

где a ® 0 при Dx ® 0.

Умножение всех членов последнего равенства на Dx дает

Dy = fў(x) Dx + aDx.

Так как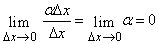, то приращение Dy функции состоит из двух слагаемых, из которых первое слагаемое есть (при f ў(x) № 0) так называемая главная часть приращения, линейная относительно Dx. Произведение f ў(x)Dx называют дифференциалом функции и обозначают через dy или df(x):

dy = f ў(x)Dx

Можно найти дифференциал функции y = x. В этом случае yў = (x)ў = 1 и, следовательно,

Dy = dx = Dx. Таким образом, дифференциал dx независимой переменной x совпадает с ее приращением Dx.

Дифференциалы различных порядков.

Дифференциал функции y = f(x), где x – независимая переменная, есть dy = f ў(x)dx, некоторая функция от x, но от x может зависеть только первый сомножитель f ў(x), второй же сомножитель (dx) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x, то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y:

d(dy) = d2y = f ўў(x)(dx)².

Дифференциалом n-го порядка называется первый дифференциал от дифференциала n- 1-го порядка:

dⁿy = d(dⁿ–1y) = f(n)(x)dx(n).

В этом случае:

полный дифференциал df

Если функция зависит не от одного, а от нескольких аргументов x_i (i изменяется от1 до n, I = 1,2,…n), f(x1, x2,…x_n), то можно рассматривать приращение функции при изменении одного или нескольких (в том числе и всех) аргументов и аналогично функции одной переменной вводить понятие дифференциала как приращения каждого из меняющихся аргументов. Тогда можно записать полный дифференциал df как линейную часть полного приращения функции при приращении всех ее аргументов

Здесь 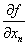– частная производная по переменной x_{n .}

Cм. также ПРОИЗВОДНАЯ.

Анна Чугайнова