ПОЛЗУЧЕСТЬ

ПОЛЗУЧЕСТЬ – медленное деформирование тела под действием постоянной нагрузки. Иногда этот термин используют в более общем смысле для обозначения неупругих процессов изменения во времени деформаций и напряжений в телах различной природы, таких как пластики, горные породы, бетон, органические материалы, лед и др. Изучением ползучести и, вообще, деформаций и текучести таких материалов занимается реология. Классическая область исследований теории ползучести – это деформации металлов и сплавов при высоких температурах.

Основной эффект можно наблюдать в таком опыте: находящийся при достаточно высокой температуре образец подвергается действию постоянной растягивающей нагрузки, в процессе опыта записывается деформация как функция времени.

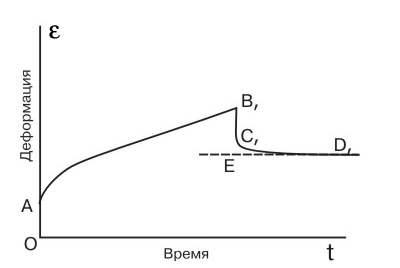
Типичная кривая ползучести представлена на рис. 1. Вертикальный отрезок OA изображает мгновенную деформацию в момент приложения нагрузки; участок кривой AB дает рост деформации во времени при постоянной нагрузке: видно, что скорость деформирования v(t), равная производной de / dt, убывает, AB – участок неустановившейся ползучести, после которой наступает установившаяся ползучесть с постоянной скоростью de / dt = const, которая существенно зависит от величины приложенного напряжения. Третий участок CD характеризуется возрастанием скорости и заканчивается разрушением образца. Деформации ползучести аналогичны пластическим деформациям с одним отличием: если полностью разгрузить образец, то обнаруживается явление возврата или обратной ползучести (рис. 2): в момент разгрузки мгновенно исчезает начальная упругая деформация (отрезок BC); после этого ненагруженный образец продолжает укорачиваться, и кривая CD, имеющая горизонтальную асимптоту ED, иллюстрирует этот процесс. Обычно деформация возврата составляет небольшую долю деформации ползучести и в расчетах ею обычно пренебрегают.

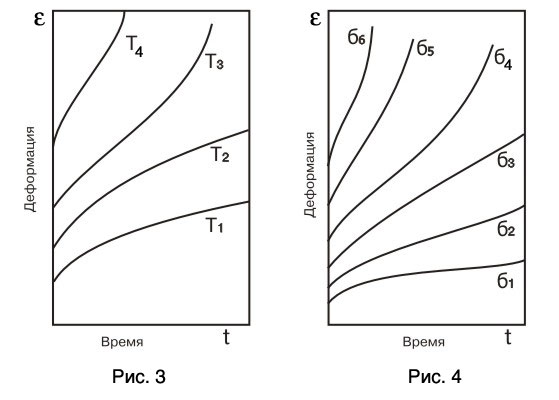
На рис. 3 и 4 приведены качественно похожие семейства кривых: первое представляет собой типичные кривые ползучести, построенные в экспериментах при одинаковой температуре, но при разных напряжениях; вторая – при одинаковых напряжениях, но различных температурах.

Скорость ползучести на установившемся участке существенно зависит от температуры и от действующего напряжения. Если аппроксимировать степенной функцией экспериментальную зависимость скорости от напряжения,

v = const s\up12n

то оказывается, что показатель n в разных случаях имеет величину от 3 до 12. Это означает, что уравнения, описывающие ползучесть металлов при высоких температурах должны быть сильно нелинейными, поэтому методы реологии, использующие в основном линейные и близкие к линейным уравнения, не используются в теории ползучести металлов, которая исторически развивалась независимо от реологии и была логически связана скорее с теорией пластичности металлов как пластичность при высоких температурах.

Релаксацией напряжений называется процесс уменьшения во времени напряжений в теле; классический опыт на релаксацию состоит в том, что образец быстро растягивают до деформации e0 и фиксируют в этом состоянии. Если температура достаточно велика, чтобы в материале происходил процесс ползучести, то обнаруживается уменьшение напряжений. Математически это следует из того, что деформация e0 = const представляется в момент t в виде суммы упругой деформации ey и деформации ползучести en: (t)

e0 = ey + en (t)

Деформация ползучести en (t) все время увеличивается, а сумма e0 остается постоянной; отсюда следует, что уменьшается первое слагаемое – упругая деформация, которая связана с напряжением s по закону Гука:

ey = s / E

Это означает, что рост enen необходимо приводит к уменьшению напряжения s.

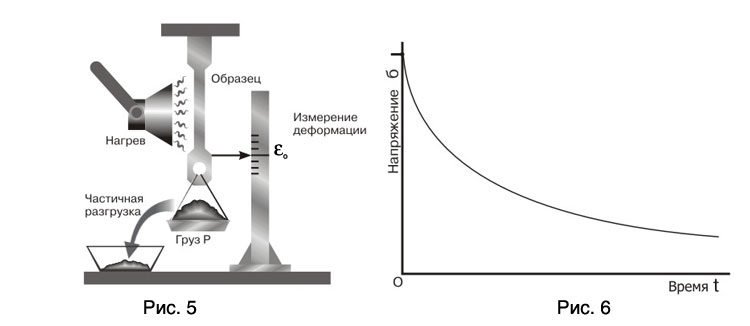
Релаксацию напряжений можно наблюдать и непосредственно в опыте, который схематически можно представить себе следующим образом: нагретый образец нагружен, как показано на рис. 5, весом чашки со свинцовой дробью. В момент нагружения возникает деформация e0, которая, за счет ползучести, начинает увеличиваться. Как только это увеличение достигает ощутимой величины De, с чашки снимается такая часть груза, чтобы деформация образца вернулась к первоначальной величине e0; эта процедура повторяется затем в течение всего опыта. Конечно, в реальных современных экспериментальных установках используются автоматические следящие системы. Результат опыта представляется в виде графика зависимости напряжение – время и называется кривой релаксации (рис. 6).

Ползучесть при постоянном напряжении и релаксация при постоянной деформации – это два предельных случая, когда же тело находится при высокой температуре под действием заданной системы нагрузок, в нем происходит изменение, перераспределение как деформаций, так и напряжений. Если внешние нагрузки не изменяются во времени, то в теле преимущественную роль играет процесс ползучести. Такая ситуация характерна для тепловых машин, особенно для газовых турбин, так как турбинные лопатки подвергаются длительному нагружению центробежными силами, действующими в одном направлении – по радиусу диска. Поскольку зазор между лопатками ротора и корпусом делается достаточно малым, ползучесть лопаток является одним из важнейших факторов, влияющих на работу турбины. Второй фактор – это материал, из которого сделаны лопатки, металловеды создали специальные сплавы, которые имеют рабочие температуры 950–1000° C. Теория ползучести должна уметь ответить на вопрос – с какой скоростью увеличивается длина лопатки в зависимости от режимы работы турбины и определить время службы (ресурс) лопатки.

С ползучестью тесно связано явление длительной прочности. Определение времени до разрушения – основная проблема теории длительной прочности, которая изучает способность материала сопротивляться разрушению при высоких температурах в условиях ползучести. Говоря о прочности сооружения или детали, работающей при нормальной температуре в стабильных условиях, исключающих ползучесть, мы по существу говорим, что разрушение не наступит неопределенно долго. Расчет по теории длительной прочности при заданном уровне напряжений гарантирует определенное время, в течение которого разрушение не произойдет.

Владимир Кузнецов