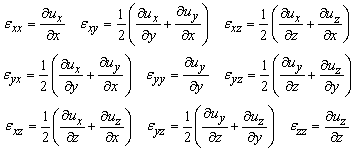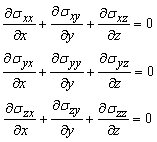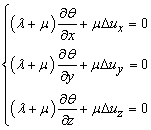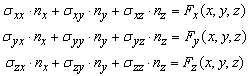ТЕОРИЯ УПРУГОСТИ

ТЕОРИЯ УПРУГОСТИ – раздел механики сплошных сред, изучающий перемещения, деформации и напряжения покоящихся или движущихся тел под действием нагрузок. Цель этой теории – вывод математических уравнений, решение которых позволяет ответить на следующие вопросы: каковы будут деформации данного конкретного тела, если к нему приложить в известных местах нагрузки заданной величины? Каковы будут при этом напряжения в теле? Вопрос в том, разрушится ли тело или выдержит эти нагрузки, тесно связан с теорией упругости, но, строго говоря, не входит в компетенцию этой теории.

Количество возможных примеров безгранично – от определения деформаций и напряжений в балке, лежащей на опорах и нагруженной силами, до расчета тех же величин в конструкции самолета, корабля, подводной лодки, в колесе вагона, в броне при ударе снаряда, в горном массиве при прохождении штольни, в каркасе высотного здания и т.д. Здесь нужно сделать оговорку: конструкции, состоящие из тонкостенных элементов, рассчитывают по упрощенным теориям, логически основанным на теории упругости; к таким теориям относятся: теория сопротивления материалов действию нагрузок (знаменитый «сопромат»), задачей которой, в основном, является расчет стержней и балок; строительная механика – расчет стержневых систем (например, мостов); и, наконец, теория оболочек – по существу, самостоятельная и очень сильно развитая область науки о деформациях и напряжениях, предмет исследования которой – важнейшие элементы конструкций – тонкостенные оболочки – цилиндрические, конические, сфероидальные, и имеющие более сложные формы. Поэтому в теории упругости обычно рассматриваются тела, у которых существенные размеры отличаются не слишком сильно. Таким образом, рассматривается упругое тело заданной формы, на которое действуют известные силы.

Основными понятиями теории упругости являются напряжения, действующие на малых площадках, которые можно мысленно провести в теле через заданную точку M, деформации малой окрестности точки M и перемещения самой точки M. Точнее говоря, вводятся тензоры напряжений sij, тензор малых деформаций eij и вектор перемещения u_i.

Краткое обозначение sij, где индексы i, j принимают значения 1, 2, 3 следует понимать как матрицу вида:

Аналогично следует понимать и краткое обозначение тензора eij.

Если физическая точка тела M вследствие деформации заняла новое положение в пространстве M´, то вектор перемещения есть вектор с компонентами (u_xu_yu_z), или, сокращенно, u_i. В теории малых деформаций компоненты u_i и ei считаются малыми величинами (строго говоря, бесконечно малыми). Компоненты тензора eij и вектора u_ij связаны формулами Коши, которые имеют вид:

Видно, что exy = eyx, и, вообще говоря, eij = eji, поэтому тензор деформаций является симметричным по определению.

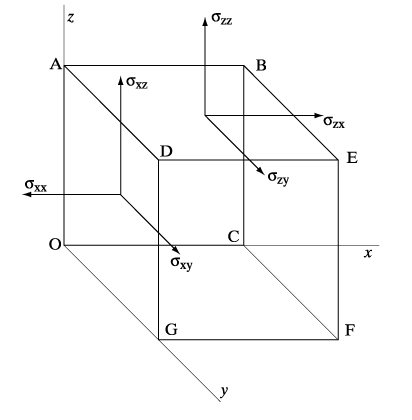
Если упругое тело под действием внешних сил находится в равновесии (т.е. скорости всех его точек равны нулю), то в равновесии находится и любая часть тела, которую можно мысленно из него выделить. Из тела выделяется маленький (строго говоря, бесконечно малый) прямоугольный параллелепипед, грани которого параллельны координатным плоскостям декартовой системы Oxyz (рис. 1).

Пусть ребра параллелепипеда имеют длины dx, dy, dz соответственно (здесь, как обычно dx есть дифференциал x, и т.д.). Согласно теории напряжений, на гранях параллелепипеда действуют компоненты тензора напряжений, которые обозначаются:

на грани OADG: sxx, sxy, sxz

на грани OABC: syx, syy, syz

на грани DABE: szx, szy, szz

при этом компоненты с одинаковыми индексами (например sxx) действуют перпендикулярно грани, а с разными индексами – в плоскости площадки.

На противоположных гранях значения одноименных компонент тензора напряжений немного отличаются, это связано с тем, что они являются функциями координат и изменяются от точки к точке (всегда, кроме известных простейших случаев), а малость изменения связана с малыми размерами параллелепипеда, поэтому можно считать, что если на грани OABC действует напряжение syy, то на грани GDEF действует напряжение syy +dsyy, причем малая величина dsyy именно в силу своей малости может быть определена с помощью разложения в ряд Тейлора:

(здесь используются частные производные, т.к. компоненты тензора напряжений зависят от x, y, z).

Аналогично можно выразить напряжения на всех гранях через sij и dsij. Далее, чтобы перейти от напряжений к силам, нужно умножить величину напряжения на площадь той площадки, на которой оно действует (например, syy + dsyy умножить на dx dz). Когда все силы, действующие на параллелепипед, определены, можно, как это делают в статике, записать уравнение равновесия тела, при этом во всех уравнениях для главного вектора останутся только члены с производными, так как сами напряжения взаимно уничтожаются, а множители dx dy dz сокращаются и в результате

Аналогично получаются уравнения равновесия, выражающие равенство нулю главного момента всех сил, действующих на параллелепипед, которые приводятся к виду:

Эти равенства означают, что тензор напряжений есть симметричный тензор. Таким образом, для 6 неизвестных компонент sij есть три уравнения равновесия, т.е. уравнений статики недостаточно для решения задачи. Выход из положения состоит в том, чтобы выразить напряжения sij через деформации eij с помощью уравнений закона Гука, а затем деформации eij выразить через перемещения u_i с помощью формул Коши, и результат подставить в уравнения равновесия. При этом получается три дифференциальных уравнения равновесия относительно трех неизвестных функций u_x u_y u_z, т.е. число неизвестных равно числу уравнений. Эти уравнения называются уравнениями Ламе

Здесь:

не учитываются массовые силы (вес и др.)

D – оператор Лапласа, то есть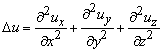

Теперь нужно задать на поверхности тела граничные условия;

основные виды этих условий следующие:

1. На известной части поверхности тела S₁ заданы перемещения, т.е. вектор перемещений равен известному вектору с компонентами {f_x; f_y; f_z}:

u_x = f(xyz)

u_y = f(xyz)

u_z = f(xyz)

(f_x, f_y, f_z– известные функции координат)

2. На остальной части поверхности S₂ заданы поверхностные силы. Это означает, что распределение напряжений внутри тела таково, что величины напряжений в непосредственной близости от поверхности, а в пределе – на поверхности на каждой элементарной площадке создают вектор напряжений, равный известному вектору внешней нагрузки с компонентами {F_x ;F_y ; F_z} поверхностных сил. Математически это записывается так: если в точке A поверхности вектор единичной нормали к этой поверхности имеет компоненты n_x, n_y, n_z то в этой точке должны быть выполнены равенства относительно (неизвестных) компонент sij:

В этих формулах появляется вектор нормали, так как компоненты тензора sij определены на площадках, параллельных координатным плоскостям, а малая площадка на поверхности ориентирована, вообще говоря, произвольно, и ее ориентация как раз и задается вектором Сами формулы получаются аналогично тому, как были получены уравнения равновесия, но исходя из равновесия малого тетраэдра, у которого три грани параллельны координатным плоскостям, а четвертая является частью поверхности тела и имеет нормаль , причем на этой площадке действует вектор внешних усилий .

В граничных условиях все компоненты напряжений sij считаются выраженными через производные от u_x, u_y, u_z как это делается при выводе уравнения Ламе.

Уравнения Ламе и граничные условия и образуют краевую задачу теории упругости, для которой, при естественных ограничениях, доказаны существование и единственность решения.

В теорию упругости входит еще одна группа уравнений – уравнения совместности деформаций. Если формулы Коши рассматривать как уравнения относительно трех неизвестных компонент перемещений u_x, u_y, u_z считая заданными шесть величин eij, то для трех неизвестных получим шесть уравнений, то есть переопределенную систему. Эта система будет иметь решение только при выполнении дополнительных условий относительно eij. Эти условия и есть уравнения совместности.

Эти уравнения часто называют условиями сплошности, подразумевая при этом, что они обеспечивают сплошность тела после деформации. Это выражение образное, но неточное: эти условия обеспечивают существование непрерывного поля перемещений, если в качестве неизвестных принять компоненты деформаций (или напряжений). Невыполнение этих условий ведет не к нарушению сплошности, а к отсутствию решения задачи.

Таким образом, теория упругости дает дифференциальные уравнения и граничные условия, которые позволяют сформулировать краевые задачи, решение которых дает полную информацию о распределении в рассматриваемых телах напряжений, деформаций и перемещений. Методы решения таких задач весьма сложны и наилучшие результаты дает сочетание аналитических методов с численными, использующими мощные компьютеры.

Владимир Кузнецов