ЧИСЕЛ ТЕОРИЯ
ЧИСЕЛ ТЕОРИЯ, раздел чистой математики, занимающийся изучением целых чисел 0, ±1, ±2,... и соотношений между ними. Иногда теорию чисел называют высшей арифметикой. Отдельные вычисления, производимые над конкретными числами, например, 9 + 16 = 25, не представляют особого интереса и обычно не входят в предмет теории чисел. С другой стороны, выписанное только что равенство становится несравненно более интересным, если заметить, что оно представляет собой простейшее решение в целых числах (если не считать тривиальных решений x = z, y = 0) уравнения Пифагора x2 + y2 = z2. С этой точки зрения последнее уравнение непосредственно приводит к некоторым подлинным теоретико-числовым проблемам, например, (1) имеет ли x2 + y2 = z2 бесконечно много или только конечное число решений в целых числах и как их можно найти? (2) Какие целые числа представимы в виде x2 + y2, где x и y – целые числа? (3) Существуют ли решения в целых числах аналогичного уравнения xn + yn = zn, где n – целое число, большее 2? Одна из интригующих особенностей теории чисел состоит в том, что эти три вопроса, формулируемые так легко и понятно, в действительности находятся на совершенно различных уровнях сложности. Пифагор и Платон, а возможно гораздо раньше вавилонские математики, знали, что уравнение x2 + y2 = z2 имеет бесконечно много решений в целых числах, а древнегреческому математику Диофанту (ок. 250 до н.э.) было известно, что каждое такое решение представимо в виде x = r2 – s2, y = 2rs, z = r2 + s2 при подходящих целых числах r и s и что при любых двух целых числах r и s соответствующие значения x, y и z образуют решение. Что касается второго вопроса, то структуру множества целых чисел, представимых в виде суммы двух квадратов, описал П.Ферма (1601–1665), основатель теории чисел в ее современной форме. Ферма показал, что целое число m представимо в виде суммы двух квадратов в том и только в том случае, когда частное от деления числа m на наибольший квадрат, делящий число m, не содержит простого множителя вида 4k + 3 (k – целое число). Этот результат гораздо тоньше, чем первый, а его доказательство далеко не очевидно, хотя и не является слишком трудным. Третий вопрос оставался без ответа, несмотря на упорнейшие усилия самых блестящих математических умов, на протяжении трех последних столетий. Ферма примерно в 1630 на полях одной из книг написал, что уравнение xn + yn = zn не имеет решений в целых числах x, y и z, отличных от нуля, при n больше 2, но самого доказательства не оставил. И только в 1994 Э.Вайлсу из Принстонского университета удалось доказать эту теорему, уже несколько веков носящую название «Великой теоремы Ферма».
Вне самой математики теория чисел имеет довольно мало приложений, и развивалась она не ради решения прикладных задач, а как искусство ради искусства, обладающее своей внутренней красотой, тонкостью и трудностью. Тем не менее теория чисел оказала большое влияние на математическую науку, поскольку некоторые разделы математики (в том числе и такие, которые впоследствии нашли применение в физике) были первоначально созданы для решения особенно сложных проблем теории чисел.
См. также ЧИСЛО; МАТЕМАТИКА.
Мультипликативные основания.
Условимся считать, что в дальнейшем все латинские буквы будут означать (если особо не оговорено противное) целые числа. Мы говорим, что b является делителем числа a (или что b делит a) и обозначаем это b|a, если существует такое целое число c, что a = bc. Числа 1 и -1 («единицы»), обратные к которым – целые числа, являются делителями любого целого числа. Если ±1 и ±a – единственные делители числа a, то оно называется простым; если же существуют другие делители, то число a называется составным. (Простыми числами являются, например, 2, 3, 5, 7, 11, 13.) Если положительное целое число a составное, то его можно представить в виде a = bc, где 1 < b < a и 1 < c < a; если либо b, либо c составное, то его в свою очередь можно разложить на множители. Продолжая разлагать на множители, мы в конце концов должны прийти к представлению числа a в виде произведения конечного числа простых чисел (не все из которых обязательно различны); например, 12 = 2Ч2Ч3, 13 = 1Ч13, 100 = 2Ч2Ч5Ч5. В противном случае число a можно было бы записать в виде произвольно большого числа множителей, каждый из которых не меньше 2, что невозможно. Теорема о единственности разложения на простые множители, одна из фундаментальных теорем теории чисел, утверждает, что с точностью до очевидных изменений в знаках и порядке множителей любые два разложения числа a совпадают; например, любое разложение числа 12 на простые множители представимо тремя числами – 2Ч2Ч3; 2Ч3Ч2; 3Ч2Ч2; другие разложения получаются заменой любых двух множителей равными по абсолютной величине отрицательными числами. Теорема о единственности разложения на простые множители встречается в «Началах» Евклида, где она доказана с помощью понятия наибольшего общего делителя (НОД). Если d > 0 – общий делитель чисел a и b и, в свою очередь, делится на любое другое число, делящее a и b, то d называется наибольшим общим делителем чисел a и b, что записывается так: НОД(a, b) = d; например, НОД (12, 18) = 6. Если НОД (a, b) = 1, то числа a и b называются взаимно простыми. Евклид показал, что для любых двух чисел a и b, отличных от нуля, существует единственный НОД, и предложил систематический метод, напоминающий «деление углом»; с НОД чисел a и b связано их наименьшее общее кратное (НОК) – наименьшее положительное число, которое делится на каждое из чисел a и b. Наименьшее общее кратное равно произведению чисел a и b, деленному на их НОД, или |ab|/НОД (a, b).
См. также АРИФМЕТИКА.
Согласно теореме о единственности разложения на простые множители, простые числа являются теми «кирпичиками», из которых строятся целые числа. Помимо ±2, все остальные простые числа нечетны, так как четным число называется только когда оно делится на 2. Уже Евклиду было известно, что простых чисел бесконечно много. Он доказал это, заметив, что число N = (p1p2...pn) + 1 (где p1, p2,..., pn – все простые числа) не делится ни на одно простое число p1, p2,..., pn и, потому либо само N, либо один из его простых множителей должен быть простым числом, отличным от p1, p2,..., pn. Следовательно, p1, p2,..., pn не может быть полным перечнем всех простых чисел.
Пусть m і 1 – некоторое заданное целое число. Любое число a при делении на m дает остаток, равный одному из чисел 0, 1, ..., m – 1. (Например, при m = 13 и a, принимающем последовательно значения 29, 7, -21, 65, получаем: 29 = 2Ч3 + 3, 7 = 0Ч13 + 7, –21 = –2Ч13 + 5, 65 = 5Ч13 + 0, и остатки равны соответственно 3, 7, 5, 0.) Если числа a и b при делении на m дают один и тот же остаток, то в некоторых случаях их можно рассматривать как эквивалентные относительно m. Математики говорят в таких случаях, что числа a и b сравнимы по модулю m, что записывается так: a є b (mod m) и называется сравнением по модулю m. Мы все знакомы со сравнением по модулю 12 в случае с часами: 17 часов означает то же самое, что 5 часов пополудни, так как 17 є 5 (mod 12). Это отношение, называемое сравнением, было введено К.Гауссом (1777–1855). Оно несколько похоже на равенство тем, что сравнения по одному и тому же модулю m можно складывать и умножать, как обычно: если a є b (mod m) и c є d (mod m), то a + c є b + d (mod m), a – c є b – d (mod m), aЧc є bЧd (mod m) и ta є tb (mod m) при любом целом t. Сокращение на общий множитель, вообще говоря, невозможно, т.к. 20 є 32 (mod 6), но 5 № 8 (mod 6). Однако если ta є tb (mod m) и (t,m) = d, то a є b (mod (m/d)). При d = 1 это по существу сводится к сокращению на общий множитель; например, 28 є 40 (mod 3), и так как числа 4 и 3 взаимно простые, мы можем разделить обе части сравнения на 4 и получить 7 є 10 (mod 3). Можно также показать, что если a є b (mod m), то НОД чисел a и m равен НОД чисел b и m. В качестве примера рассмотрим сравнение 6 є 10 (mod 4): НОД (6, 4) равен 2, и НОД (10, 4) также равен 2.
Все целые числа, сравнимые с каким-либо числом, образуют один класс вычетов. Для каждого модуля m существует m классов вычетов, соответствующих m остаткам 0, 1,..., m - 1; каждый из классов содержит одно из чисел 0, 1,..., m – 1 вместе со всеми числами, сравнимыми с этим числом по модулю m. Если два числа a и b принадлежат одному классу вычетов, т.е. удовлетворяют соотношению a є b (mod m), то НОД (a,m) = НОД (b,m); следовательно, либо все элементы данного класса вычетов взаимно просты с m, либо ни один не взаимно прост. Число «приведенных» классов вычетов, т.е. классов вычетов, элементы которых взаимно просты с m, обозначается f (m). Таким образом возникает функция на множестве целых чисел, называемая f-функцией Эйлера в честь Л.Эйлера (1707–1783). При m = 6 существует шесть классов вычетов, каждый из которых содержит одно из чисел 0, 1,..., 5. С этим m взаимно просты только элементы класса, содержащего число 5, и класса, содержащего число 1. Следовательно, f (m) = 2.
Как и в случае уравнений, можно рассматривать сравнения с одним или более неизвестными. Простейшим служит линейное сравнение с одним неизвестным ax є b (mod m). Оно выполняется только в том случае, когда m делит число (ax – b), или ax – b = my при некотором целом y. Таким образом, это сравнение эквивалентно линейному уравнению ax – my = b. Так как левая его часть обязательно делится на НОД (a, m), оно не может выполняться ни при каких целых числах x и y, если НОД (a, m) не делит число b.
Можно показать, что сравнение ax є b (mod m) разрешимо в том и только в том случае, когда НОД (a, m) делит число b, а если это условие выполнено, то существует ровно НОД (a, m) классов вычетов по модулю m, элементы которых удовлетворяют этому сравнению. Например, уравнение 2x + 6y = 5 неразрешимо в целых числах, т.к. НОД (2, 6) = 2, а число 5 не делится на 2; уравнение 2x + 3y = 5 разрешимо, т.к. НОД (2, 3) = 1; аналогично, уравнение 2x + 3y = b разрешимо при любом целом b. Действительно, при любых a и m, таких, что НОД (a, m) = 1, уравнение ax – my = b разрешимо для любого b.
Уравнение ax – my = b – это, по-видимому, простейший пример «диофантова уравнения», т.е. уравнения с целыми коэффициентами, которое требуется решить в целых числах.
Общее квадратичное сравнение ax2 + bx + c є 0 (mod m) можно проанализировать весьма полно. Умножая на 4a, получаем 4a2x2 + 4abx + 4ac є 0 (mod 4am), или (2ax + b)2є (b2 – 4ac) (mod 4am). Полагая 2ax + b = u и b2 – 4ac = r, мы сводим решение исходного сравнения к решению сравнения u2є r (mod 4am). В свою очередь решения последнего сравнения с помощью чуть более сложных рассуждений можно свести к решению сравнений вида u2є r (mod p), где p – простое число. Поэтому все сложности и весь интерес кроются в этом, казалось бы, частном случае общего квадратичного сравнения. Если сравнение u2є r (mod p) разрешимо, то u называется квадратичным вычетом по модулю p, а в противном случае – квадратичным невычетом. «Квадратичный закон взаимности», открытый эмпирически Эйлером (ок. 1772) и доказанный Гауссом (1801), утверждает, что если p и q – различные нечетные простые числа, то каждое из них или является квадратичным вычетом по модулю другого, или это не верно ни для одного из них за исключением случая, когда и p, и q имеют вид 4k + 3 и когда лишь одно из этих чисел является квадратичным вычетом по модулю другого. Теорема Гаусса, названная им «золотой теоремой», служит мощным инструментом теоретико-числовых исследований и позволяет ответить на вопрос, разрешимо ли данное квадратичное сравнение.
Сравнения более высоких степеней вида f (x) є 0 (mod m), где f (x) – многочлен степени выше 2, решаются с большим трудом. Согласно теореме Ж.Лагранжа (1736–1813), число решений (точнее, число классов вычетов, каждый из элементов которых является решением) не превышает степени многочлена f (x), если модуль простой. Существует простой критерий разрешимости сравнения xn є r (mod p), принадлежащий Эйлеру, но он неприменим к сравнениям общего вида, о разрешимости которых при n > 2 мало что известно.
Диофантовы уравнения.
Несмотря на то, что исследования диофантовых уравнений восходят к началу становления математики, общая теория диофантовых уравнений до сих пор отсутствует. Вместо этого имеется обширный набор отдельных приемов, каждый из которых полезен при решении лишь ограниченного класса задач. Приступая к изучению диофантова уравнения, хотелось бы получить описание всех его целочисленных решений, как это было сделано выше для уравнения x2 + y2 = z2. В этом смысле полностью решить удалось лишь небольшой класс уравнений, большинство из которых либо линейно, либо квадратично. Решение произвольной системы из m линейных уравнений с n неизвестными в случае, когда n > m, было получено Г.Смитом (1826–1883). Простейшим квадратным уравнением является т.н. уравнение Пелля x2 – Dy2 = N (где D и N – любые целые числа), которое было полностью решено Лагранжем (1766). Известны также решения различных отдельных уравнений или систем уравнений второй степени с более чем двумя неизвестными, а также немногих уравнений более высоких степеней. В последнем случае получены в основном отрицательные результаты – рассматриваемое уравнение не имеет решений или имеет только конечное число решений. В частности, К.Зигель показал в 1929, что единственными алгебраическими уравнениями с двумя неизвестными, имеющими бесконечно много целочисленных решений, являются линейные уравнения, уравнения Пелля и уравнения, получаемые из тех и других с помощью специальных преобразований.
Формы.
Формой называется однородный многочлен от двух или более переменных, т.е. многочлен, все члены которого имеют одну и ту же полную степень по совокупности переменных; например, x2 + xy + y2 – форма степени 2, x3 – x2y + 3xy2 + y3 – форма степени 3. Одним из основных является вопрос, аналогичный сформулированному выше для формы x2 + y2, а именно: какие целые числа представимы с помощью формы (т.е. какие целые значения может принимать форма) при целых значениях переменных? И на этот раз наиболее полно был рассмотрен квадратичный случай. Для простоты мы ограничимся лишь двумя переменными, т.е. формами вида f(x,y) = ax2 + bxy + cy2. Величина D = 4ac – b2 называется дискриминантом формы f(x,y); если дискриминант равен нулю, то форма вырождается в квадрат линейной формы. Такой случай обычно не рассматривается. Формы с положительным дискриминантом называются определенными, т.к. все значения, принимаемые формой f(x,y) в этом случае, имеют тот же знак, что и a; при положительном a форма f(x,y) всегда положительна и называется положительно определенной. Формы с отрицательным дискриминантом называются неопределенными, так как f(x,y) принимает как положительные, так и отрицательные значения.
Если в f(x,y) произвести замену переменных x = Au + Bv, y = Cu + Dv, где A, B, C, D – целые числа, удовлетворяющие условию AD – BC = ±1, то получим новую форму g(u,v). Так как любой паре целых чисел x и y соответствует пара целых чисел u и v, то каждое целое число, представимое формой f, представимо формой g, и наоборот. Поэтому в таком случае говорят, что f и g эквивалентны. Все формы, эквивалентные данной, образуют класс эквивалентности; число таких классов для форм с фиксированным дискриминантом D конечно.
Оказывается, что в случае положительно определенных форм в каждом классе эквивалентности существует единственная форма ax2 + bxy + cy2 с такими коэффициентами a, b, c, что либо –a < b Ј a < c, либо 0 Ј b Ј a = c. Такая форма называется приведенной формой данного класса эквивалентности. Приведенная форма используется как стандартный представитель своего класса, а информация, получаемая относительно нее, легко распространяется на остальные члены класса эквивалентности. Одной из основных задач, которая в этом простейшем случае полностью решена, является нахождение приведенной формы, эквивалентной данной форме; этот процесс называется приведением. В случае неопределенных форм мы не можем указать неравенств, которым должны удовлетворять коэффициенты лишь одной формы из каждого класса. Однако существуют неравенства, которым удовлетворяет некоторое конечное число форм в каждом классе, и все они называются приведенными формами.
Определенные и неопределенные формы различаются также тем, что любая определенная форма представляет (если представляет) целое число только конечным числом способов, тогда как число представлений целого числа неопределенной формой всегда либо равно нулю, либо бесконечно. Дело в том, что, в отличие от определенных форм, неопределенные обладают бесконечно многими «автоморфизмами», т.е. подстановками x = Au + Bv, y = Cu + Dv, оставляющими форму f (x,y) неизменной, так что f (x,y) = f (u,v). Эти автоморфизмы можно полностью описать в терминах решений уравнения Пелля z2 + Dw2 = 4, где D – дискриминант формы f.
Некоторые частные результаты, связанные с представлением целых чисел квадратичными формами, были известны задолго до появления только что описанной общей теории, начало которой было положено Лагранжем в 1773 и которая получила развитие в работах Лежандра (1798), Гаусса (1801) и других. Ферма в 1654 показал, что каждое простое число вида 8n + 1 или 8n + 3 представимо формой x2 + 2y2, каждое простое число вида 3n + 1 представимо формой x2 + 3y2 и не существует простого числа вида 3n – 1, представимого формой x2 + 3y2. Он также установил, что любое простое число вида 4n + 1 представимо, причем единственным способом, в виде суммы двух квадратов. Ферма не оставил доказательств этих теорем (как, впрочем, и почти всех других своих результатов). Некоторые из них были доказаны Эйлером (1750–1760), причем доказательство последней из указанных теорем потребовало от него семи лет напряженных усилий. Ныне эти теоремы известны как простые следствия из квадратичного закона взаимности.
Сходным образом можно определить и эквивалентность квадратичных форм от n переменных. Существуют аналогичные теории приведения и представлений, естественно, более сложные, чем в случае двух переменных. К 1910 развитие теории продвинулось настолько, насколько это было возможно с помощью классических методов, и теория чисел пребывала в состоянии спячки вплоть до 1935, когда Зигель придал ей новый импульс, сделав основным инструментом исследований в этой области математический анализ.
Одна из наиболее удивительных теорем теории чисел была доказана Ферма и, по-видимому, была известна еще Диофанту. Она гласит, что любое целое число есть сумма четырех квадратов. Более общее утверждение без доказательства высказал Э.Варинг (1734–1798): каждое положительное целое число есть сумма не более девяти кубов, не более девятнадцати четвертых степеней и т.д. Общее утверждение о том, что для каждого положительного целого числа k существует целое число s, такое, что любое положительное целое число может быть представлено в виде суммы не более чем s k-х степеней, было в конце концов доказано Д.Гильбертом (1862–1943) в 1909.
Геометрия чисел.
В общих чертах можно сказать, что геометрия чисел включает в себя все приложения геометрических понятий и методов к теоретико-числовым проблемам. Отдельные соображения такого рода появились в 19 в. в работах Гаусса, П.Дирихле, Ш.Эрмита и Г.Минковского, в которых для решения некоторых неравенств или систем неравенств в целых числах использовались их геометрические интерпретации. Минковский (1864–1909) систематизировал и унифицировал все, сделанное в этой области до него, и нашел новые важные приложения, особенно в теории линейных и квадратичных форм. Он рассматривал n неизвестных как координаты в n-мерном пространстве. Множество точек с целыми координатами получило название решетки. Все точки с координатами, удовлетворяющими требуемым неравенствам, Минковский интерпретировал как внутренность некоторого «тела», и задача состояла в том, чтобы определить, содержит ли данное тело какие-либо точки решетки. Фундаментальная теорема Минковского утверждает, что если тело выпукло и симметрично относительно начала координат, то оно содержит хотя бы одну точку решетки, отличную от начала координат, при условии, что n-мерный объем тела (при n = 2 это площадь) больше, чем 2n.
Многие вопросы естественно приводят к теории выпуклых тел, и именно эта теория была развита Минковским наиболее полно. Затем на долгое время опять наступил застой, но с 1940, в основном благодаря работам английских математиков, наметился прогресс в развитии теории невыпуклых тел.
Диофантовы приближения.
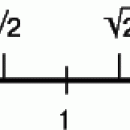
Этот термин был введен Минковским для описания задач, в которых некоторое переменное выражение должно быть сделано насколько возможно малым, когда переменная принимает целочисленные значения, не превышающие некоторого большого числа N. В настоящее время термин «диофантовы приближения» используется в более широком смысле для обозначения ряда теоретико-числовых задач, в которых встречается одно или несколько заданных иррациональных чисел. (Иррациональным называется число, которое нельзя представить в виде отношения двух целых чисел.) Почти все такого рода проблемы возникли из следующего фундаментального вопроса: если дано некоторое иррациональное число q, то каковы наилучшие рациональные приближения к нему и насколько хорошо они его приближают? Разумеется, если использовать достаточно сложные рациональные числа, то число q можно приблизить сколь угодно точно; поэтому вопрос имеет смысл только в том случае, когда точность приближения сопоставляется с величиной числителя или знаменателя, аппроксимирующего числа. Например, 22/7 – хорошее приближение к числу p в том смысле, что из всех рациональных чисел со знаменателем 7 дробь 22/7 ближе всех к числу p. Такие хорошие приближения всегда можно найти с помощью разложения числа q в непрерывную дробь. Подобные разложения, в чем-то похожие на разложения в десятичную дробь, служат мощным инструментом исследований в современной теории чисел. С их помощью, например, нетрудно убедиться в том, что для каждого иррационального числа q существует бесконечно много дробей y/x, таких, что погрешность |q – y/x| меньше, чем 1/x2 (см. также НЕПРЕРЫВНЫЕ ДРОБИ).
Число b называется алгебраическим, если оно удовлетворяет некоторому алгебраическому уравнению с целочисленными коэффициентами a0bn + a1bn – 1 +... + an = 0. В противном случае число b называется трансцендентным. То немногое, что известно о трансцендентных числах, получено с помощью методов диофантовых приближений. Доказательства обычно сводятся к нахождению аппроксимационных свойств трансцендентных чисел, которыми не обладают алгебраические числа. Примером может служить теорема Ж.Лиувилля (1844), согласно которой число b трансцендентно, если при сколь угодно большом показателе n найдется дробь y/x, такая, что 0 < |b – y/x| < 1/xn. Развивая идеи Эрмита, Ф.Линдеман в 1882 доказал, что число p трансцендентно и тем самым дал окончательный (отрицательный) ответ на вопрос, поставленный еще древними греками: можно ли с помощью циркуля и линейки построить квадрат, равный по площади данному кругу? В 1934 А.О.Гельфонд (1906–1968) и Т.Шнайдер (р. 1911) независимо друг от друга доказали, что если алгебраическое число a, отличное от 0 или 1, возвести в иррациональную алгебраическую степень b, то получившееся число ab трансцендентно. Например, число ![]() трансцендентно. То же самое можно сказать и о ep (значении выражения i–2i).
трансцендентно. То же самое можно сказать и о ep (значении выражения i–2i).
Аналитическая теория чисел.
Математический анализ можно назвать математикой непрерывно изменяющихся величин; поэтому на первый взгляд может показаться странным, что при решении чисто теоретико-числовых задач такая математика может быть полезной. Первым, кто стал систематически использовать весьма мощные аналитические методы в арифметике, был П.Дирихле (1805–1859). Исходя из свойств «рядов Дирихле»
рассматриваемых как функции переменной s, он показал, что если НОД (a,m) = 1, то существует бесконечно много простых чисел вида p є a (mod m) (таким образом, существует бесконечно много простых чисел вида 4k + 1, а также бесконечно много простых чисел вида 4k + 3). Частный случай ряда Дирихле 1 + 2–s + 3–s +... получил название дзета-функция Римана z (s) в честь Б.Римана (1826–1866), который исследовал ее свойства при комплексном s, чтобы проанализировать распределение простых чисел. Задача состоит в следующем: если p (x) обозначает число простых чисел, не превышающих x, то как велико значение p (x) при больших значениях x? В 1798 А.Лежандр высказал предположение, согласно которому отношение p(x) к x/log x (где логарифм берется по основанию e) приближенно равно 1 и с возрастанием x стремится к 1. Частичный результат был получен в 1851 П.Л.Чебышёвым (1821–1894), но полностью гипотеза Лежандра, т.н. «теорема о простых числах», была доказана лишь в 1896 с помощью методов, основанных на работе Римана (независимо Ж.Адамаром и Ш. де ла Валле Пуссеном). В 20 в. в области аналитической теории чисел было сделано немало, однако многие, казалось бы, легкие вопросы относительно простых чисел по-прежнему остаются без ответа. Например, поныне неизвестно, существует ли бесконечно много «пар простых чисел», т.е. пар последовательных простых чисел, таких, как 101 и 103. Существует еще одна до сих пор недоказанная гипотеза Римана, она касается комплексных чисел, являющихся нулями дзета-функции, и занимает настолько важное место во всей теории, что многие доказанные и опубликованные теоремы содержат слова «Если гипотеза Римана верна, то...».
Аналитические методы широко применяются и в аддитивной теории чисел, занимающейся представлениями чисел в виде сумм определенного вида. Аналитические методы были существенно использованы Гильбертом в его решении проблемы Варинга, о которой упоминалось выше. Попытки придать теореме Гильберта количественный характер с помощью оценки числа k-х степеней, необходимых для представления всех целых чисел, привели в 1920-х и 1930-х годах Г.Харди и Дж.Литлвуда к созданию кругового метода, усовершенствованного далее И.М.Виноградовым (1891–1983). Эти методы нашли применение в аддитивной теории простых чисел, например, при доказательстве теоремы Виноградова о том, что каждое достаточно большое нечетное число представимо в виде суммы трех простых чисел.
Алгебраическая теория чисел.
Чтобы доказать закон взаимности четвертых степеней (аналог квадратичного закона взаимности для соотношения x4є q (mod p)), Гаусс в 1828 исследовал арифметику комплексных чисел a + bi, где a и b – обычные целые числа, а ![]() . Делимость, «единицы», простые числа и НОД для «гауссовых чисел» определяются так же, как для обычных целых чисел, сохраняется также и теорема о единственности разложения на простые числа. Пытаясь доказать Великую теорему Ферма (о том, что уравнение xn + yn = zn не имеет решений в целых числах при n > 2), Э.Куммер в 1851 перешел к изучению арифметики целых чисел более общего типа, определяемых с помощью корней из единицы. Сначала Куммер полагал, что ему удалось найти доказательство теоремы Ферма, но он заблуждался, поскольку, вопреки наивной интуиции, для таких чисел не выполняется теорема о единственности разложения на простые множители. В 1879 Р.Дедекинд ввел общее понятие алгебраического целого числа, т.е. алгебраического числа, удовлетворяющего алгебраическому уравнению с целочисленными коэффициентами и коэффициентом a0 при старшем члене, равном 1. Чтобы получить некоторое множество алгебраических целых чисел, аналогичное множеству обычных целых чисел, необходимо рассматривать только такие алгебраические целые числа, которые принадлежат фиксированному полю алгебраических чисел. Это множество всех чисел, которые можно получить из некоторого данного числа и рациональных чисел с помощью многократного применения сложения, вычитания, умножения и деления; поле алгебраических чисел аналогично множеству рациональных чисел. Алгебраические целые числа из данного поля в свою очередь подразделяются на «единицы», простые и составные числа, но в общем случае для двух таких чисел однозначно определенного НОД не существует и не выполняется теорема о единственности разложения на простые множители. Простейшие примеры полей алгебраических чисел, кроме множества рациональных чисел, это поля алгебраических чисел, определенные с помощью алгебраических чисел степени 2, т.е. иррациональных чисел, удовлетворяющих квадратным уравнениям с рациональными коэффициентами. Такие поля называются квадратичными числовыми полями.
. Делимость, «единицы», простые числа и НОД для «гауссовых чисел» определяются так же, как для обычных целых чисел, сохраняется также и теорема о единственности разложения на простые числа. Пытаясь доказать Великую теорему Ферма (о том, что уравнение xn + yn = zn не имеет решений в целых числах при n > 2), Э.Куммер в 1851 перешел к изучению арифметики целых чисел более общего типа, определяемых с помощью корней из единицы. Сначала Куммер полагал, что ему удалось найти доказательство теоремы Ферма, но он заблуждался, поскольку, вопреки наивной интуиции, для таких чисел не выполняется теорема о единственности разложения на простые множители. В 1879 Р.Дедекинд ввел общее понятие алгебраического целого числа, т.е. алгебраического числа, удовлетворяющего алгебраическому уравнению с целочисленными коэффициентами и коэффициентом a0 при старшем члене, равном 1. Чтобы получить некоторое множество алгебраических целых чисел, аналогичное множеству обычных целых чисел, необходимо рассматривать только такие алгебраические целые числа, которые принадлежат фиксированному полю алгебраических чисел. Это множество всех чисел, которые можно получить из некоторого данного числа и рациональных чисел с помощью многократного применения сложения, вычитания, умножения и деления; поле алгебраических чисел аналогично множеству рациональных чисел. Алгебраические целые числа из данного поля в свою очередь подразделяются на «единицы», простые и составные числа, но в общем случае для двух таких чисел однозначно определенного НОД не существует и не выполняется теорема о единственности разложения на простые множители. Простейшие примеры полей алгебраических чисел, кроме множества рациональных чисел, это поля алгебраических чисел, определенные с помощью алгебраических чисел степени 2, т.е. иррациональных чисел, удовлетворяющих квадратным уравнениям с рациональными коэффициентами. Такие поля называются квадратичными числовыми полями.
Куммеру принадлежит фундаментальная идея введения новых т.н. идеальных чисел (1847), выбираемых таким образом, чтобы в расширенном множестве снова выполнялась теорема о единственности разложения на простые множители. Для той же цели Дедекинд в 1870 ввел несколько иное понятие идеалов, а Кронекер в 1882 – метод разложения многочлена с рациональными коэффициентами на неприводимые множители над полем рациональных чисел. Работы этих трех математиков не только заложили основы арифметической теории алгебраических чисел, но и ознаменовали начало современной абстрактной алгебры.
Вопрос о том, имеет ли место в данном поле единственное разложение на простые множители, весьма труден. Ситуация ясна только в одном случае: существует лишь конечное число квадратичных полей, обладающих этим свойством, и все такие поля, за исключением одного сомнительного случая, хорошо известны. С «единицами» поля ситуация проще: как показал Дирихле, все «единицы» (которых, вообще говоря, бесконечно много) можно представить в виде произведений степеней некоторого конечного множества «единиц». Рассмотрение такого рода проблем в связи с каким-нибудь конкретным полем непременно предваряет более глубокие арифметические исследования в рамках этого поля и приложения к проблемам классической теории чисел. Существует другая, более тонкая теория, начало которой было положено в 1894 Гильбертом, в которой одновременно рассматриваются все числовые поля, обладающие определенными свойствами. Она называется «теорией полей классов» и принадлежит к наиболее строгим в техническом отношении разделам математики. Существенный вклад в ее развитие внесли Ф.Фуртвенглер в 1902 и Т.Такаги в 1920. В последние годы в этой области математики наблюдается значительная активность.
Виноградов И.М. Основы теории чисел. М., 1981
Шафаревич И.Р. Теория чисел. М., 1985
Ответь на вопросы викторины «Математика»