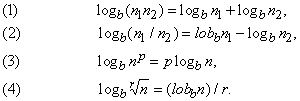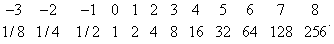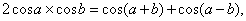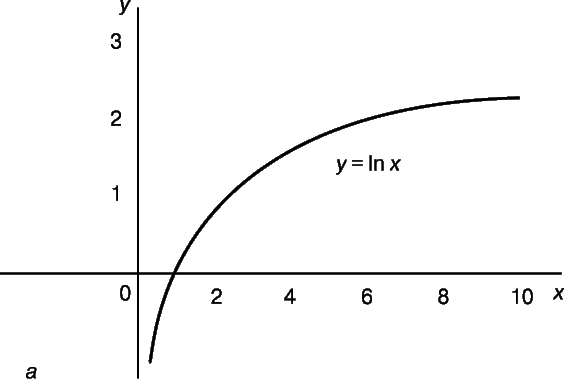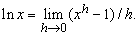ЛОГАРИФМ
ЛОГАРИФМ, число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление – вычитанием, возведение в степень – умножением и извлечение корней – делением.
Общее описание.
Логарифмом данного числа называется показатель степени, в которую нужно возвести другое число, называемое основанием логарифма, чтобы получить данное число. Например, логарифм числа 100 по основанию 10 равен 2. Иначе говоря, 10 нужно возвести в квадрат, чтобы получить число 100 (102 = 100). Если n – заданное число, b – основание и l – логарифм, то bl = n. Число n также называется антилогарифмом по основанию b числа l. Например, антилогарифм 2 по основанию 10 равен 100. Сказанное можно записать в виде соотношений logb n = l и antilogb l = n.
Основные свойства логарифмов:
Любое положительное число, кроме единицы, может служить основанием логарифмов, но, к сожалению, оказывается, что если b и n – рациональные числа, то в редких случаях найдется такое рациональное число l, что bl = n. Однако можно определить иррациональное число l, например, такое, что 10l = 2; это иррациональное число l можно с любой требуемой точностью приблизить рациональными числами. Оказывается, что в приведенном примере l примерно равно 0,3010, и это приближенное значение логарифма по основанию 10 числа 2 можно найти в четырехзначных таблицах десятичных логарифмов. Логарифмы по основанию 10 (или десятичные логарифмы) столь часто используются при вычислениях, что их называют обычными логарифмами и записывают в виде log2 = 0,3010 или lg2 = 0,3010, опуская явное указание основания логарифма. Логарифмы по основанию e, трансцендентному числу, приближенно равному 2,71828, называются натуральными логарифмами. Они встречаются преимущественно в работах по математическому анализу и его приложениям к различным наукам. Натуральные логарифмы также записывают, не указывая явно основание, но используя специальное обозначение ln: например, ln2 = 0,6931, т.к. e0,6931 = 2. См. также ЧИСЛО e.
Пользование таблицами обычных логарифмов.
Обычный логарифм числа – это показатель степени, в которую нужно возвести 10, чтобы получить данное число. Так как 100 = 1, 101 = 10 и 102 = 100, мы сразу получаем, что log1 = 0, log10 = 1, log100 = 2 и т.д. для возрастающих целых степеней 10. Аналогично, 10–1 = 0,1, 10–2 = 0,01 и, следовательно, log0,1 = –1, log0,01 = –2 и т.д. для всех целых отрицательных степеней 10. Обычные логарифмы остальных чисел заключены между логарифмами ближайших к ним целых степеней числа 10; log2 должен быть заключен между 0 и 1, log20 – между 1 и 2, а log0,2 – между -1 и 0. Таким образом, логарифм состоит из двух частей, целого числа и десятичной дроби, заключенной между 0 и 1. Целочисленная часть называется характеристикой логарифма и определяется по самому числу, дробная часть называется мантиссой и может быть найдена из таблиц. Кроме того, log20 = log(2ґ10) = log2 + log10 = (log2) + 1. Логарифм числа 2 равен 0,3010, поэтому log20 = 0,3010 + 1 = 1,3010. Аналогично, log0,2 = log(2ё10) = log2 – log10 = (log2) – 1 = 0,3010 – 1. Выполнив вычитание, мы получим log0,2 = – 0,6990. Однако удобнее представить log0,2 в виде 0,3010 – 1 или как 9,3010 – 10; можно сформулировать и общее правило: все числа, получающиеся из данного числа умножением на степень числа 10, имеют одинаковые мантиссы, равные мантиссе заданного числа. В большинстве таблиц приведены мантиссы чисел, лежащих в интервале от 1 до 10, поскольку мантиссы всех остальных чисел могут быть получены из приведенных в таблице.
В большинстве таблиц логарифмы даются с четырьмя или пятью десятичными знаками, хотя существуют семизначные таблицы и таблицы с еще бóльшим числом знаков. Научиться пользоваться такими таблицами легче всего на примерах. Чтобы найти log3,59, прежде всего заметим, что число 3,59 заключено между 100 и 101, поэтому его характеристика равна 0. Находим в таблице число 35 (слева) и движемся по строке до столбца, у которого сверху стоит число 9; на пересечении этого столбца и строки 35 стоит число 5551, поэтому log3,59 = 0,5551. Чтобы найти мантиссу числа с четырьмя значащими цифрами, необходимо прибегнуть к интерполяции. В некоторых таблицах интерполирование облегчается пропорциональными частями, приведенными в последних девяти столбцах в правой части каждой страницы таблиц. Найдем теперь log736,4; число 736,4 лежит между 102 и 103, поэтому характеристика его логарифма равна 2. В таблице находим строку, слева от которой стоит 73 и столбец 6. На пересечении этой строки и этого столбца стоит число 8669. Среди линейных частей находим столбец 4. На пересечении строки 73 и столбца 4 стоит число 2. Прибавив 2 к 8669, получим мантиссу – она равна 8671. Таким образом, log736,4 = 2,8671.
Натуральные логарифмы.
Таблицы и свойства натуральных логарифмов аналогичны таблицам и свойствам обычных логарифмов. Основное различие между теми и другими состоит в том, что целочисленная часть натурального логарифма не имеет существенного значения при определении положения десятичной запятой, и поэтому различие между мантиссой и характеристикой не играет особой роли. Натуральные логарифмы чисел 5,432; 54,32 и 543,2 равны, соответственно, 1,6923; 3,9949 и 6,2975. Взаимосвязь между этими логарифмами станет очевидной, если рассмотреть разности между ними: log543,2 – log54,32 = 6,2975 – 3,9949 = 2,3026; последнее число есть не что иное, как натуральный логарифм числа 10 (пишется так: ln10); log543,2 – log5,432 = 4,6052; последнее число равно 2ln10. Но 543,2 = 10ґ54,32 = 102ґ5,432. Таким образом, по натуральному логарифму данного числа a можно найти натуральные логарифмы чисел, равные произведениям числа a на любые степени n числа 10, если к lna прибавлять ln10, умноженный на n, т.е. ln(aґ10n) = lna + nln10 = lna + 2,3026n. Например, ln0,005432 = ln(5,432ґ10–3) = ln5,432 – 3ln10 = 1,6923 – (3ґ2,3026) = – 5,2155. Поэтому таблицы натуральных логарифмов, как и таблицы обычных логарифмов, обычно содержат только логарифмы чисел от 1 до 10. В системе натуральных логарифмов можно говорить об антилогарифмах, но чаще говорят об экспоненциальной функции или об экспоненте. Если x = lny, то y = ex, и y называется экспонентой от x (для удобства типографского набора часто пишут y = exp x). Экспонента играет роль антилогарифма числа x.
С помощью таблиц десятичных и натуральных логарифмов можно составить таблицы логарифмов по любому основанию, отличному от 10 и e. Если logb a = x, то bx = a, и, следовательно, logc bx = logc a или xlogc b = logc a, или x = logc a/logc b = logb a. Следовательно, с помощью этой формулы обращения из таблицы логарифмов по основанию c можно построить таблицы логарифмов по любому другому основанию b. Множитель 1/logc b называется модулем перехода от основания c к основанию b. Ничто не мешает, например, пользуясь формулой обращения, или перехода от одной системы логарифмов к другой, найти натуральные логарифмы по таблице обычных логарифмов или совершить обратный переход. Например, log105,432 = loge 5,432/loge 10 = 1,6923/2,3026 = 1,6923ґ0,4343 = 0,7350. Число 0,4343, на которое нужно умножить натуральный логарифм данного числа, чтобы получить обычный логарифм, является модулем перехода к системе обычных логарифмов.
Специальные таблицы.
Первоначально логарифмы были изобретены для того, чтобы, пользуясь их свойствами logab = loga + logb и loga/b = loga – logb, превращать произведения в суммы, а частные в разности. Иначе говоря, если loga и logb известны, то с помощью сложения и вычитания мы легко можем найти логарифм произведения и частного. В астрономии, однако, часто по заданным значениям loga и logb требуется найти log(a + b) или log(a – b). Разумеется, можно было бы сначала по таблицам логарифмов найти a и b, затем выполнить указанное сложение или вычитание и, снова обратившись к таблицам, найти требуемые логарифмы, но такая процедура потребовала бы трехкратного обращения к таблицам. З.Леонелли в 1802 опубликовал таблицы т.н. гауссовых логарифмов – логарифмов сложения сумм и разностей – позволявшие ограничиться одним обращением к таблицам.
В 1624 И.Кеплером были предложены таблицы пропорциональных логарифмов, т.е. логарифмов чисел a/x, где a – некоторая положительная постоянная величина. Эти таблицы используются преимущественно астрономами и навигаторами.
Пропорциональные логарифмы при a = 1 называются кологарифмами и применяются в вычислениях, когда приходится иметь дело с произведениями и частными. Кологарифм числа n равен логарифму обратного числа; т.е. cologn = log1/n = – logn. Если log2 = 0,3010, то colog2 = – 0,3010 = 0,6990 – 1. Преимущество использования кологарифмов состоит в том, что при вычислении значения логарифма выражений вида pq/r тройная сумма положительных десятичных долей logp + logq + cologr находится легче, чем смешанная сумма и разность logp + logq – logr.
История.
Принцип, лежащий в основе любой системы логарифмов, известен очень давно и может быть прослежен в глубь истории вплоть до древневавилонской математики (около 2000 до н.э.). В те времена интерполяция между табличными значениями целых положительных степеней целых чисел использовалась для вычисления сложных процентов. Гораздо позже Архимед (287–212 до н.э.) воспользовался степенями числа 108 для нахождения верхнего предела числа песчинок, необходимого для того, чтобы целиком заполнить известную в те времена Вселенную. Архимед обратил внимание на свойство показателей степеней, лежащее в основе эффективности логарифмов: произведение степеней соответствует сумме показателей степеней. В конце Средних веков и начале Нового времени математики все чаще стали обращаться к соотношению между геометрической и арифметической прогрессиями. М.Штифель в своем сочинении Арифметика целых чисел (1544) привел таблицу положительных и отрицательных степеней числа 2:
Штифель заметил, что сумма двух чисел в первой строке (строке показателей степени) равна показателю степени двойки, отвечающему произведению двух соответствующих чисел в нижней строке (строке степеней). В связи с этой таблицей Штифель сформулировал четыре правила, эквивалентных четырем современным правилам операций над показателями степеней или четырем правилам действий над логарифмами: сумма в верхней строке соответствует произведению в нижней строке; вычитание в верхней строке соответствует делению в нижней строке; умножение в верхней строке соответствует возведению в степень в нижней строке; деление в верхней строке соответствует извлечению корня в нижней строке.
По-видимому, правила, аналогичные правилам Штифеля, привели Дж.Нейпера к формальному введению первой системы логарифмов в сочинении Описание удивительной таблицы логарифмов, опубликованном в 1614. Но мысли Непера были заняты проблемой превращения произведений в суммы еще с тех пор, как более чем за десять лет до выхода своего сочинения Непер получил из Дании известие о том, что в обсерватории Тихо Браге его ассистенты располагают методом, позволяющим превращать произведения в суммы. Метод, о котором говорилось в полученном Непером сообщении, был основан на использовании тригонометрических формул типа
поэтому таблицы Нейпера состояли главным образом из логарифмов тригонометрических функций. Хотя понятие основания не входило в явном виде в предложенное Непером определение, роль, эквивалентную основанию системы логарифмов, в его системе играло число (1 – 10–7)ґ107, приближенно равное 1/e.
Независимо от Нейпера и почти одновременно с ним система логарифмов, довольно близкая по типу, была изобретена и опубликована Й.Бюрги в Праге, издавшем в 1620 Таблицы арифметической и геометрической прогрессий. Это были таблицы антилогарифмов по основанию (1 + 10–4) ґ104, достаточно хорошему приближению числа e.
В системе Нейпера логарифм числа 107 был принят за нуль, и по мере уменьшения чисел логарифмы возрастали. Когда Г.Бриггс (1561–1631) навестил Непера, оба согласились, что было бы удобнее использовать в качестве основания число 10 и считать логарифм единицы равным нулю. Тогда с увеличением чисел их логарифмы возрастали бы. Таким образом мы получили современную систему десятичных логарифмов, таблицу которых Бриггс опубликовал в своем сочинении Логарифмическая арифметика (1620). Логарифмы по основанию e, хотя и не совсем те, которые были введены Нейпером, часто называют нейперовыми. Термины «характеристика» и «мантисса» были предложены Бриггсом.
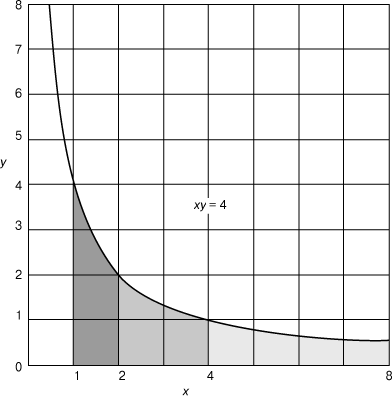
Первые логарифмы в силу исторических причин использовали приближения к числам 1/e и e. Несколько позднее идею натуральных логарифмов стали связывать с изучением площадей под гиперболой xy = 1 (рис. 1). В 17 в. было показано, что площадь, ограниченная этой кривой, осью x и ординатами x = 1 и x = a (на рис. 1 эта область покрыта более жирными и редкими точками) возрастает в арифметической прогрессии, когда a возрастает в геометрической прогрессии. Именно такая зависимость возникает в правилах действий над экспонентами и логарифмами. Это дало основание называть нейперовы логарифмы «гиперболическими логарифмами».
Логарифмическая функция.
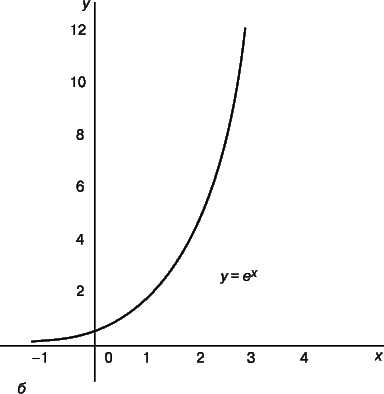
Было время, когда логарифмы рассматривались исключительно как средство вычислений, однако в 18 в., главным образом благодаря трудам Эйлера, сформировалась концепция логарифмической функции. График такой функции y = lnx, ординаты которого возрастают в арифметической прогрессии, тогда как абсциссы – в геометрической, представлен на рис. 2,а. График обратной, или показательной (экспоненциальной), функции y = ex, ординаты которого возрастают в геометрической прогрессии, а абсциссы – в арифметической, представлен, соответственно, на рис. 2,б. (Кривые y = logx и y = 10x по форме аналогичны кривым y = lnx и y = ex.) Были предложены также альтернативные определения логарифмической функции, например,
Благодаря работам Эйлера стали известны соотношения между логарифмами и тригонометрическими функциями в комплексной плоскости. Исходя из тождества eix = cos x + i sin x (где угол x измеряется в радианах, 
), Эйлер заключил, что каждое отличное от нуля действительное число имеет бесконечно много натуральных логарифмов; все они являются комплексными в случае отрицательных чисел и все, кроме одного, – в случае положительных чисел. Поскольку eix = 1 не только при x = 0, но и при x = ± 2kp, где k – любое положительное целое число, за натуральный логарифм числа 1 можно принять любое из чисел 0 ± 2kpi; и, аналогично, натуральные логарифмы числа -1 являются комплексными числами вида (2k + 1)pi, где k – целое число. Аналогичные утверждения справедливы и относительно общих логарифмов или других систем логарифмов. Кроме того, определение логарифмов можно обобщить, пользуясь тождествами Эйлера так, чтобы оно включало комплексные логарифмы комплексных чисел.
Альтернативное определение логарифмической функции дает функциональный анализ. Если f (x) – непрерывная функция действительного числа x, обладающая следующими тремя свойствами: f (1) = 0, f (b) = 1, f (uv) = f (u) + f (v), то f (x) определяется как логарифм числа x по основанию b. Это определение обладает рядом преимуществ перед определением, приведенным в начале этой статьи.
Приложения.
Логарифмы первоначально использовались исключительно для упрощения вычислений, и это их приложение до сих пор остается одним из самых главных. Вычисление произведений, частных, степеней и корней облегчается не только благодаря широкой доступности опубликованных таблиц логарифмов, но и благодаря использованию т.н. логарифмической линейки – вычислительного инструмента, принцип работы которого основан на свойствах логарифмов. Линейка снабжена логарифмическими шкалами, т.е. расстояние от числа 1 до любого числа x выбрано равным log x; сдвигая одну шкалу относительно другой, можно откладывать суммы или разности логарифмов, что дает возможность считывать непосредственно со шкалы произведения или частные соответствующих чисел. Воспользоваться преимуществами представления чисел в логарифмическом виде позволяет и т.н. логарифмическая бумага для построения графиков (бумага с нанесенными на нее по обеим осям координат логарифмическими шкалами). Если функция удовлетворяет степенному закону вида y = kxn, то ее логарифмический график имеет вид прямой, т.к. log y = log k + n log x – уравнение, линейное относительно log y и log x. Наоборот, если логарифмический график какой-нибудь функциональной зависимости имеет вид прямой, то эта зависимость – степенная. Полулогарифмическая бумага (у которой ось ординат имеет логарифмическую шкалу, а ось абсцисс – равномерную шкалу) удобна в тех случаях, когда требуется идентифицировать экспоненциальные функции. Уравнения вида y = kbrx возникают всякий раз, когда некая величина, такая как численность населения, количество радиоактивного материала или банковский баланс, убывает или возрастает со скоростью, пропорциональной имеющемуся в данный момент количеству жителей, радиоактивного вещества или денег. Если такую зависимость нанести на полулогарифмическую бумагу, то график будет иметь вид прямой.
Логарифмическая функция возникает в связи с самыми разными природными формами. По логарифмическим спиралям выстраиваются цветки в соцветиях подсолнечника, закручиваются раковины моллюска Nautilus, рога горного барана и клювы попугаев. Все эти природные формы могут служить примерами кривой, известной под названием логарифмической спирали, потому что в полярной системе координат ее уравнение имеет вид r = aebq, или lnr = lna + bq. Такую кривую описывает движущаяся точка, расстояние от полюса которой растет в геометрической прогрессии, а угол, описываемый ее радиусом-вектором – в арифметической. Повсеместность такой кривой, а следовательно и логарифмической функции, хорошо иллюстрируется тем, что она возникает в столь далеких и совершенно различных областях, как контур кулачка-эксцентрика и траектория некоторых насекомых, летящих на свет.
Ответь на вопросы викторины «Математика»