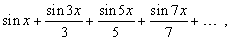РЯДЫ
РЯДЫ. Многие задачи в математике приводят к формулам, содержащим бесконечные суммы, например,
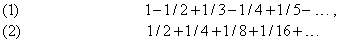
или
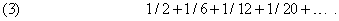
Такие суммы называются бесконечными рядами, а их слагаемые – членами ряда. (Многоточие означает, что число слагаемых бесконечно.) Решения сложных математических задач редко удается представить в точном виде посредством формул. Однако в большинстве случаев эти решения можно записать в виде рядов. После того, как такое решение найдено, методы теории рядов позволяют оценить, сколько членов ряда необходимо взять для конкретных вычислений или как записать ответ в наиболее удобном виде. Наряду с числовыми рядами мы можем рассматривать т.н. функциональные ряды, слагаемыми которых являются функции. Многие функции можно представить с помощью функциональных рядов. Изучение числовых и функциональных рядов является важной частью математического анализа.
В примерах (1) и (2) сравнительно легко догадаться, по какому закону образуются последовательные члены. Закон образования членов ряда может быть гораздо менее очевидным. Например, для ряда (3) он станет ясен, если этот ряд записать в следующем виде:
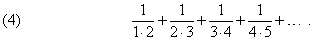
Сходящиеся ряды.
Поскольку сложение бесконечного числа членов ряда физически невозможно, необходимо определить, что именно следует понимать под суммой бесконечного ряда. Можно представить себе, что указанные операции сложения и вычитания выполняются последовательно, одна за другой, например, на компьютере. Если возникающие при этом суммы (частичные суммы) все ближе и ближе подходят к некоторому числу, то это число разумно назвать суммой бесконечного ряда. Таким образом, сумму бесконечного ряда можно определить как предел последовательности частичных сумм. При этом такой ряд называется сходящимся.
Найти сумму ряда (3) нетрудно, если заметить, что преобразованный ряд (4) можно записать в виде
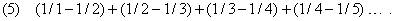
Последовательные частичные суммы ряда (5) равны
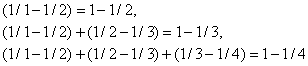
и т.д.; можно заметить, что частичные суммы стремятся к 1. Таким образом, этот ряд сходится и его сумма равна 1.
В качестве примера бесконечных рядов можно рассматривать бесконечные десятичные дроби. Так, 0,353535... – это бесконечная периодическая десятичная дробь, являющаяся компактным способом записи ряда
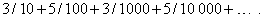
Закон образования последовательных членов здесь понятен. Аналогично, 3,14159265... означает
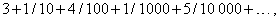
но закон образования последующих членов ряда здесь неочевиден: цифры образуют десятичное разложение числа p, и трудно сразу сказать, какова, например, 100 000-я цифра, хотя теоретически эту цифру можно вычислить.
Расходящиеся ряды.
О бесконечном ряде, который не сходится, говорят, что он расходится (такой ряд называют расходящимся). Например, ряд
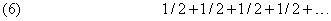
расходится, так как его частичные суммы равны 1/2, 1, 11/2, 2,.... Эти суммы не стремятся ни к какому числу как к пределу, поскольку, взяв достаточно много членов ряда, мы можем сделать частичную сумму сколь угодно большой. Ряд

также расходится, но по другой причине: частичные суммы этого ряда попеременно обращаются то в 1, то в 0 и не стремятся к пределу.
Суммирование.
Найти сумму сходящегося ряда (с заданной точностью), последовательно суммируя его члены, хотя теоретически и возможно, но практически трудно осуществимо. Например, ряд
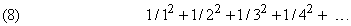
сходится, и сумма его с точностью до десяти знаков после запятой равна 1,6449340668, но для того, чтобы вычислить ее с этой точностью, потребовалось бы взять ок. 20 млрд. членов. Такие ряды обычно суммируют, первоначально преобразуя их с помощью различных приемов. При этом используют алгебраические или вычислительные методы; например, можно показать, что сумма ряда (8) равна p 2/6.
Обозначения.
Работая с бесконечными рядами, полезно иметь удобные обозначения. Например, конечную сумму ряда (8) можно записать как
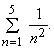
Такая запись указывает на то, что n последовательно полагается равным 1, 2, 3, 4 и 5, а результаты складываются:
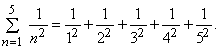
Аналогично, ряд (4) можно записать в виде
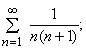
где символ Ґ указывает на то, что мы имеем дело с бесконечным рядом, а не с конечной его частью. Символ S (сигма) называют знаком суммирования.
Бесконечная геометрическая прогрессия.
Мы смогли просуммировать ряд (4), так как существовала простая формула для его частичных сумм. Аналогично, можно найти сумму ряда (2), или в общем виде,
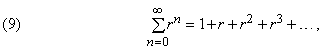
если r принимает значения между –1 и 1. В этом случае сумма ряда (9) равна 1/(1 – r); при других значениях r ряд (9) расходится.
Можно рассматривать периодические десятичные дроби вроде 0,353535... как иной способ записи бесконечной геометрической прогрессии
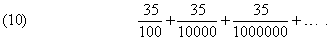
Это выражение можно записать также в виде
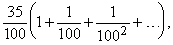
где в скобках стоит ряд (9) с r = 0,01; следовательно, сумма ряда (10) равна
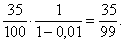
Тем же способом можно представить в виде обычной дроби любую периодическую десятичную дробь.
Признаки сходимости.
В общем случае простой формулы для частичных сумм бесконечного ряда не существует, так что для установления сходимости или расходимости ряда прибегают к специальным методам. Например, если все члены ряда положительны, то можно показать, что ряд сходится, если каждый его член не превосходит соответствующего члена другого ряда, о котором известно, что он сходится. В принятых обозначения это можно записать следующим образом: если an і 0 и 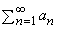 сходится, то
сходится, то 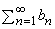 сходится, если 0 Ј bn Ј an. Например, так как ряд (4) сходится и
сходится, если 0 Ј bn Ј an. Например, так как ряд (4) сходится и
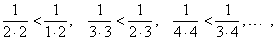
то можно сделать вывод, что ряд (8) тоже сходится. Сравнение представляет собой основной метод, позволяющий устанавливать сходимость многих рядов, сопоставляя их с простейшими сходящимися рядами. Иногда используют более специальные признаки сходимости (их можно найти в литературе по теории рядов.) Приведем еще несколько примеров сходящихся рядов с положительными членами:
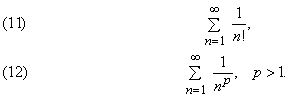
Сравнение можно использовать и для установления расходимости ряда. Если ряд 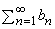 расходится, то и ряд
расходится, то и ряд 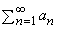 также расходится, если 0 Ј bn Ј an.
также расходится, если 0 Ј bn Ј an.
Примерами расходящихся рядов могут служить ряды

и, в частности, т.к. гармонический ряд

В расходимости этого ряда можно убедиться, сосчитав следующие частичные суммы:
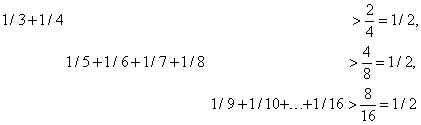
и т.д. Таким образом, частичные суммы, которые оканчиваются членами 1/4, 1/8, 1/16, 1/32, ј , превосходят частичные суммы расходящегося ряда (6), и поэтому ряд (14) должен расходиться.
Абсолютная и условная сходимости.
К таким рядам, как
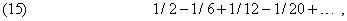
метод сравнения неприменим, поскольку члены этого ряда имеют разные знаки. Если бы все члены ряда (15) были положительными, то мы получили бы ряд (3), о котором известно, что он сходится. Можно показать, что отсюда следует также сходимость ряда (15). Когда изменением знаков отрицательных членов ряда на противоположные его можно превратить в сходящийся, говорят, что исходный ряд сходится абсолютно.
Знакопеременный гармонический ряд (1) не является абсолютно сходящимся, т.к. ряд (14), состоящий из тех же, но только положительных членов, не сходится. Однако с помощью специальных признаков сходимости для знакопеременных рядов можно показать, что ряд (1) в действительности сходится. Сходящийся ряд, который не сходится абсолютно, называется условно сходящимся.
Операции с рядами.
Исходя из определения сходящегося ряда, легко показать, что его сходимость не нарушится от вычеркивания или приписывания к нему конечного числа членов, а также от умножения или деления всех членов ряда на одно и то же число (разумеется, деление на 0 исключается). При любой перестановке членов абсолютно сходящегося ряда его сходимость не нарушается, а сумма не меняется. Например, так как сумма ряда (2) равна 1, сумма ряда
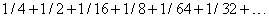
также равна 1, поскольку этот ряд получается из ряда (2) перестановкой соседних членов (1-го члена со 2-м и т.д.). Можно как угодно изменять порядок следования членов абсолютно сходящегося ряда, лишь бы в новом ряду присутствовали все члены исходного. С другой стороны, перестановка членов условно сходящегося ряда может изменить его сумму и даже сделать его расходящимся. Более того, члены условно сходящегося ряда всегда можно переставить так, что он будет сходиться к любой заранее заданной сумме.
Два сходящихся ряда San и Sbn можно почленно складывать (или вычитать), так что сумма нового ряда (который также сходится) складывается из сумм исходных рядов, в наших обозначениях
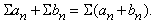
При дополнительных условиях, например, если оба ряда абсолютно сходятся, их можно умножать друг на друга, как это делается для конечных сумм, причем получающийся двойной ряд (см. ниже) будет сходиться к произведению сумм исходных рядов.
Суммируемость.
Несмотря на то, что принятое нами определение сходимости бесконечного ряда кажется естественным, оно не является единственно возможным. Сумму бесконечного ряда можно определить и другими способами. Рассмотрим, например, ряд (7), который может быть записан компактно в виде
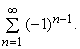
Как мы уже говорили, его частичные суммы попеременно принимают значения 1 и 0, и поэтому ряд не сходится. Но если мы образуем поочередно попарные средние его частичных сумм (текущее среднее), т.е. вычислим сначала среднее значение первой и второй частичных сумм, затем среднее второй и третьей, третьей и четвертой и т.д., то каждое такое среднее будет равно 1/2, и поэтому предел попарных средних также окажется равным 1/2. В этом случае говорят, что ряд суммируем указанным методом и его сумма равна 1/2. Было предложено много методов суммирования, позволяющих приписывать суммы довольно обширным классам расходящихся рядов и тем самым использовать некоторые расходящиеся ряды в вычислениях. Для большинства целей способ суммирования полезен, однако, только в том случае, если применительно к сходящемуся ряду он дает его конечную сумму.
Ряды с комплексными членами.
До сих пор мы молчаливо предполагали, что имеем дело лишь с действительными числами, но все определения и теоремы применимы и к рядам с комплексными числами (за исключением того, что суммы, которые могут быть получены при перестановке членов условно сходящихся рядов, не могут принимать произвольные значения).
Функциональные ряды.
Как мы уже отмечали, членами бесконечного ряда могут быть не только числа, но и функции, например,
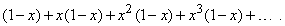
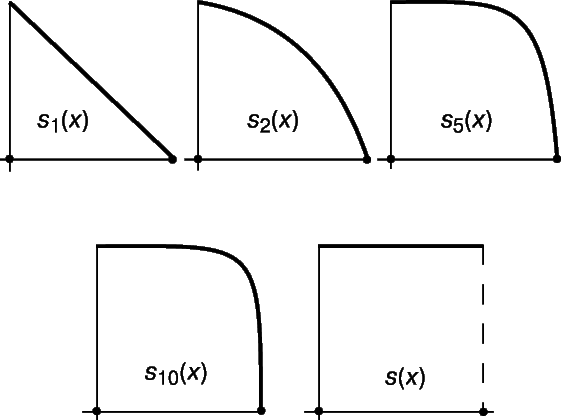
Суммой такого ряда также является функция, значение которой в каждой точке получается как предел вычисленных в этой точке частичных сумм. На рис. 1 показаны графики нескольких частичных сумм и суммы ряда (при x, изменяющемся от 0 до 1); sn(x) означает сумму первых n членов. Сумма ряда представляет собой функцию, равную 1 при 0 Ј x < 1 и 0 при x = 1. Функциональный ряд может сходиться при одних значениях x и расходиться при других; в рассмотренном нами примере ряд сходится при –1Ј x <1 и расходится при других значения x.
Сумму функционального ряда можно понимать по-разному. В некоторых случаях важнее знать, что частичные суммы близки (в том или ином смысле) к некоторой функции на всем интервале (a, b), чем доказывать сходимость или расходимость ряда в отдельных точках. Например, обозначив частичную сумму n-го порядка через sn(x), мы говорим, что ряд сходится в среднем квадратичном к сумме s(x), если
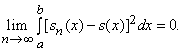
Ряд может сходиться в среднем квадратичном, даже если он не сходится ни в одной отдельной точке. Существуют также и другие определения сходимости функционального ряда.
Некоторые функциональные ряды получили название по тем функциям, которые в них входят. В качестве примера можно привести степенные ряды и их суммы:
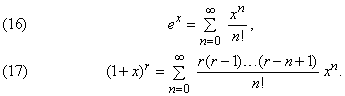
Первый из этих рядов сходится при всех x. Второй ряд сходится при |x| < 1, если r < –1; при –1Ј x < 1, если –1 < r < 0; и при |x| Ј 1, если r > 0 (за исключением тех случаев, когда r – неотрицательное целое число; в последнем случае ряд обрывается после конечного числа членов). Формула (17) называется биномиальным разложением для произвольной степени.
Ряды Дирихле.
Рядами Дирихле называются функциональные ряды вида S (1/anx), где числа an неограниченно возрастают; примером ряда Дирихле может служить дзета-функция Римана
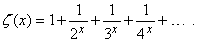
Ряды Дирихле часто используются в теории чисел.
Тригонометрические ряды.
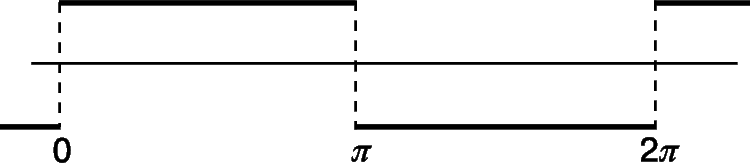
Так называются функциональные ряды, содержащие тригонометрические функции; тригонометрические ряды специального вида, используемые в гармоническом анализе, называются рядами Фурье. Примером ряда Фурье может служить ряд
суммой которого является «прямоугольная волна» (рис. 2). На рис. 3 представлены несколько первых частичных сумм и показано, как они аппроксимируют сумму ряда.
Асимптотические ряды.
Ряд
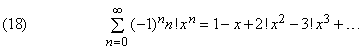
расходится при всех значения x (кроме нуля). Иначе говоря, если мы выберем какое-то значение x и начнем последовательно суммировать члены ряда, то частичные суммы не будут стремится к пределу. Однако бывает, что в этом случае существует весьма сложная функция f(x), обладающая следующим свойством: если мы возьмем конкретную частичную сумму ряда (18), например сумму первых трех его членов, то разность между f(x) и этой частичной суммой, вычисленной при некотором значении x, будет мала при всех значениях x вблизи 0. Иначе говоря, хотя мы не может добиться хорошей аппроксимации функции f(x) в какой-либо конкретной точке x, далекой от нуля, взяв даже очень много членов ряда, но при x, близком к 0, всего лишь несколько его членов дают весьма хорошее ее приближение. Такие ряды называются асимптотическими. В численных расчетах асимптотические ряды обычно полезнее, чем сходящиеся, поскольку они с помощью небольшого числа членов обеспечивают достаточно хорошее приближение. Асимптотические ряды широко используются в теории вероятностей и математической физике.
Двойные ряды.
Иногда приходится суммировать двумерные массивы чисел
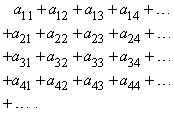
Мы можем просуммировать по строкам, а затем сложить построчные суммы. Вообще говоря, у нас нет особых оснований отдавать предпочтение строкам перед столбцами, но если суммирование сначала проводить по столбцам, то результат может оказаться другим. Например, рассмотрим двойной ряд
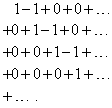
Здесь каждая строка сходится к сумме, равной 0, и сумма построчных сумм поэтому также равна нулю. С другой стороны, сумма членов первого столбца равна 1, а всех остальных столбцов равна 0, поэтому сумма сумм по столбцам равна 1. Единственными «удобными» сходящимися двойными рядами являются абсолютно сходящиеся двойные ряды: их можно суммировать по строкам или столбцам, равно как и любым другим способом, и сумма всегда получается одной и той же. Какого-либо естественного определения условной сходимости двойных рядов не существует.
Маркушевич А.И. Ряды. Элементарный очерк. М., 1957
Зигмунд А. Тригонометрические ряды, тт. 1–2. М., 1965
Мандельбройт С. Ряды Дирихле. Принципы и методы. М., 1973
Кудрявцев Л.Д. Курс математического анализа, тт. 1–2. М., 1981
Эдвардс Р. Ряды Фурье в современном изложении, тт. 1–2. М., 1985
Ответь на вопросы викторины «Математика»