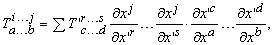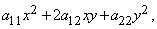ТЕНЗОР

ТЕНЗОР, в математике величина, обладающая компонентами в каждой из заданного множества систем координат, причем компоненты при переходе от одной системы координат к другой преобразуются по определенному закону. Тензорное исчисление, или «абсолютное дифференциальное исчисление», позволяет ученым формулировать и рассматривать общековариантные физические законы, остающиеся в силе при переходе от одной системы координат к другой. Тензоры определяются в геометрических пространствах любого числа измерений и играют важную роль в дифференциальной геометрии, квантовой механике, небесной механике, механике жидкостей, теории упругости и особенно в общей теории относительности. Частными случаями тензоров являются векторы и скаляры.

Основы тензорного исчисления были заложены в работах К.Гаусса (1777–1855) по геометрии поверхностей. Г.Грассман (1809–1877) расширил теорию чисел, включив в нее тензорную алгебру, а Б.Риман (1826–1866), используя гауссовы внутренние координаты, превратил n-мерные многообразия в главный объект своей новаторской работы по основаниям геометрии. Важный шаг к созданию общего тензорного исчисления сделал Э.Кристоффель (1829–1900) в своих работах по преобразованиям (эквивалентности) дифференциальных квадратичных форм. В 1890-х годах итальянский геометр Г.Риччи-Курбастро (1853–1925) и его бывший ученик Т.Леви-Чивита (1873–1941) обобщили и систематизировали результаты своих предшественников. Плодом их совместных усилий стал опубликованный в 1900 курс тензорного исчисления.

В общем случае тензор имеет вид 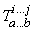. Закон его преобразования определяется соотношением

где T – преобразованный тензор, Tў – тензор до преобразования, xў – старые координаты, x – новые координаты и S означает суммирование по всем индексам. Говорят, что T – тензор, контравариантный по индексам i...j и ковариантный по индексам a...b.

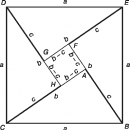
Геометрическим примером тензора могут служить коэффициенты любой квадратичной алгебраической формы, например,

относительно линейных преобразований координат.

Можно привести два примера тензора из физики: это (1) тензор инерции, компонентами которого являются моменты и произведения инерции твердого тела, и (2) тензор напряжений, компоненты которого описывают напряжения, возникающие в упругом теле под действием внешних сил. См. также ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ; ВЕКТОР.