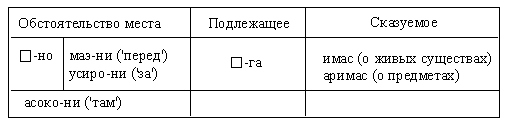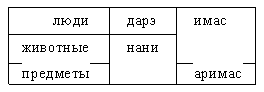ЛИНГВИСТИЧЕСКИЕ ЗАДАЧИ

Содержание статьи

• Задача № 1
• Решение задачи № 1
• Задача № 2
• Решение задачи № 2
• Задача № 3
• Решение задачи № 3
• Задача № 4
• Решение задачи № 4
• Задача № 5
• Решение задачи № 5
• Задача № 6
• Решение задачи № 6
• Задача № 7
• Решение задачи № 7
• Задача № 8
• Решение задачи № 8
• Задача № 9
• Решение задачи № 9
• Задача № 10
• Решение задачи № 10

ЛИНГВИСТИЧЕСКИЕ ЗАДАЧИ, особый жанр лингвистической учебной литературы; в том же значении употребляются термины «самодостаточные лингвистические задачи» и «самодостаточные задачи». Самодостаточная задача представляет собой особый тип задачи, существенно отличаясь от задач и упражнений проверочного характера, которые издавна использовались в процессе преподавания лингвистических дисциплин.

В термине самодостаточная задача существенны оба составляющие его слова. Это задача, потому что, в отличие от разного рода упражнений и заданий, ее нужно решать, т.е. ответ не лежит на поверхности, а достигается в результате определенных логических операций, при этом решающий может (с известной степенью строгости) доказать правильность ответа. Самодостаточность задачи проявляется в том, что весь материал, необходимый для ее решения, содержится в условии и от решающего не требуется никаких дополнительных специальных знаний или подготовки. Самодостаточная лингвистическая задача воплощает, таким образом, принцип проблемного обучения, моделируя в упрощенных условиях многие элементы творческой деятельности лингвиста, и является эффективным средством развития навыков лингвистического анализа. Что же требуется для решения таких задач? Решающий должен обладать языковой интуицией и уметь логически рассуждать.

Оригинальный жанр самодостаточной лингвистической задачи начал складываться в 1950-е годы и впервые был представлен задачником Г.Глисона в 1955; большую роль в создании жанра сыграл выдающийся лингвист, ныне академик РАН А.А.Зализняк, опубликовавший серию задач в 1963, а впоследствии предложивший немало замечательных задач для традиционной олимпиады по лингвистике и математике для школьников. Именно с этой олимпиадой и связана дальнейшая теоретическая и практическая разработка жанра. Первая олимпиада была проведена в 1965 на отделении структурной и прикладной лингвистики МГУ по инициативе талантливого лингвиста А.Н.Журинского, тогда студента 4-го курса этого отделения. Им же были подготовлены и почти все задачи первой олимпиады. А.Н.Журинский и в дальнейшем продолжал заниматься составлением задач и разработкой теории самодостаточных задач и по праву считается теоретиком жанра. Со второй олимпиады в составлении задач принимают участие и другие лингвисты. Каждая задача – оригинальное авторское произведение, однако она обязательно проверяется, обсуждается и рецензируется задачной комиссией, совершенно особым коллективом единомышленников-энтузиастов, в работе которого на равных правах принимают участие и известные ученые, и студенты. Одна из целей проверки задачи – убедиться в отсутствии паразитических решений, которые являются серьезным недостатком задачи. Часто обнаружение паразитического решения требует большой внимательности и отстраненного взгляда на языковой материал.

В ноябре-декабре 2001 состоится 32 олимпиада. С 1989 олимпиады проводятся совместно МГУ и РГГУ. К этому времени накоплено около 800 задач, и их авторами являются десятки лингвистов. Преподаватели, знакомые с этим жанром, охотно используют олимпиадные задачи на занятиях со школьниками в кружках, на факультативах, даже на уроках, и многие дети с энтузиазмом принимают такую форму работы. Ведь знания, полученные в результате пусть совсем маленького, но собственного исследования, как правило, усваиваются значительно лучше, чем преподнесенные в готовом виде учителем.

Решающий задачу знакомится с используемыми в лингвистике способами анализа языкового материала, самостоятельно «открывает» многие лингвистические понятия, такие, как фонема, морфема, согласование, сингармонизм, каузативность, и многие другие, хотя в самом материале задачи специальные термины не используются, и он доступен для начинающего.

Очень важна и другая особенность задач: они знакомят решающего с большим кругом языковых явлений, принадлежащих самым различным языкам. Накопленные за 35 лет задачи охватывают материал более двухсот языков мира. Задачи затрагивают различные разделы лингвистики: фонетику и графику, морфологию и синтаксис, семантику и историю языка; дают представление об основных системах письменности; знакомят с некоторыми проблемами современной лингвистики, в том числе с ее прикладными аспектами; отражают связь лингвистики с математикой.

Одним из наиболее распространенных типов самодостаточной лингвистической задачи является билингва. В сборнике Г.Глисона этот тип практически единственный. Решение задачи-билингвы наиболее прямолинейно (хотя и в упрощенной форме) воспроизводит деятельность лингвиста, осмысляющего материал незнакомого языка. Условие такой задачи – слова или фразы незнакомого языка с переводом на другой язык (чаще всего русский). Билингва обычно иллюстрирует какое-либо грамматическое явление незнакомого языка, которое решающему предлагается обнаружить самому в результате анализа материала из условия. Правильность проведенного анализа проверяется выполнением контрольных переводов – с русского на незнакомый и с незнакомого на русский. Задача № 1 представляет собой классический тип билингвы.

Задача № 1

(автор Е.Н.Саввина)

Даны предложения на алюторском языке с переводами на русский язык:

Переведите на алюторский язык:

1. Мы догнали соседей.

2. Соседи позвали вас.

3. Я обидел собак.

Решение задачи № 1

Существительные изменяются по числам и вдобавок имеют разную форму в зависимости от того, соответствуют ли они русскому подлежащему или дополнению: ед. число – 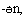мн. число подлежащего – дополнения –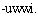

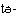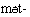Глаголы изменяются по лицу-числу подлежащего (приставкой) и по лицу-числу дополнения (суффиксом). Приставки: 'я', 'мы', 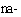'они'. Суффиксы: 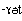'тебя', 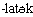'вас', 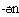'его', 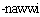'их'. Таким образом, в алюторском языке мы наблюдаем двойное согласование: сказуемое согласуется не только с подлежащим, как в русском я зыке, но и с дополнением.

Ответ:

Оригинальную форму имеет следующая билингва.

Задача № 2

(автор В.И.Беликов)

Один таитянин, будучи в Москве проездом, заинтересовался Лингвистической Олимпиадой и попросил определить, что значат таитянские слова i и e. Для этого он предложил следующие фразы с переводом на русский язык:

Листок, на котором были написаны фразы, размок под дождем. Может быть, Вам удастся восстановить отсутствующие строчки и выполнить просьбу таитянина?

Решение задачи № 2

В таитянском утвердительном предложении порядок слов следующий: сказуемое – подлежащее – дополнение (в пассиве – производитель действия); в отрицательном предложении: отрицание – подлежащее – сказуемое – дополнение (производитель действия). Перед глаголом стоит показатель времени (i – прошедшее, e – будущее); если сказуемое выражено существительным, то при нем имеется показатель е; возможно, этот показатель зависит от времени, но в условии задачи иллюстрируется только настоящее («вневременное»?) именное сказуемое. Если глагол стоит в пассиве, то он имеет после себя показатель hia. Существительное имеет в препозиции показатель te; если оно обозначает множественное число, то вслед за te следует показатель mau; прямые дополнения вводятся показателем i, деятель при пассивном глаголе – показателем е. Из условия задачи выявляется также одна интересная особенность таитянской лексики: существует два глагола со значением 'есть, принимать пищу', один употребляется по отношению к людям (tamaa), другой – по отношению к животным (ai). Отрицание выступает в четырех формах: aita – прошедшее время, aore – прошедшее усиленное, eita – будущее, eore – значение не известно, но из системных соображений можно предположить «будущее усиленное».

Отсутствующие в тексте фразы восстанавливаются следующим образом:

1. Это сильная кошка.

2. Конечно же, собака не будет есть бананы.

3. Aore teie uri i hohoni i te mau moa.

4. E tamaa te taata i te maia.

5. Eita teie matie e ai hia e te mau puaa.

Слова i и e многозначны; i является глагольным показателем прошедшего времени и показателем объекта, е – показателем будущего времени при глаголе, настоящего времени при именном сказуемом (или вообще именного сказуемого), показателем деятеля в пассивной конструкции.

Нестандартна и форма следующей билингвы.

Задача № 3

(автор Е.В.Муравенко)

Взгляните на иллюстрацию к хорошо знакомой Вам сказке «Репка».

Ниже на японском языке (в русской транскрипции) даны вопросы о взаимном расположении участников сказки и исчерпывающие ответы на эти вопросы. Все вопросы и некоторые ответы переведены на русский язык.

Вопросы и ответы на японском языке

(1)	кабура-но маэ-ни нани-га аримас ка?	Что находится перед репкой?
	асоко-ни иэ-га аримас.	<...>
(2)	нэко-но маэ-ни нани-га аримас ка?	Что находится перед кошкой?
	асоко-ни иэ-то кабура-га аримас.	<...>
(3)	маго-но маэ-ни дарэ-га имас ка?	Кто находится перед внучкой?
	асоко-ни дзидзи:-то оба:сан-га имас.	Там находятся дед и бабка.
(4)	маго-но усиро-ни нани-га имас ка?	Кто находится за внучкой?
	асоко-ни дзутика-то нэко-то нэдзуми-га имас.	<...>
(5)	нэко-но усиро-ни нани-га имас ка?	Кто находится за кошкой?
	асоко-ни нэдзуми-га имас.	<...>
(6)	нэдзуми-но усиро-ни дарэ-га имас ка?	Кто находится за мышкой?
	асоко-ни дарэ-мо имасэн.	Там никого нет
1. Переведите на русский язык все остальные ответы.
2. Переведите следующие вопросы на японский язык и дайте на них исчерпывающие ответы на японском языке. Если возможно, дайте несколько вариантов перевода и ответов:
(1)	Что находится за репкой?
(2)	Кто находится за репкой?

Решение задачи № 3

Порядок слов в японском предложении ( – обозначение существительного):

В вопросительном предложении на месте подлежащего стоит вопросительное местоимение (дарэ или нани), в конце добавляется показатель ка.

В отрицательном предложении подлежащее выступает с показателем -мо, к глаголу добавляется окончание -эн.

Если в качестве подлежащего выступает группа однородных членов, то только к последнему из них присоединяется показатель -га, остальные имеют показатель -то.

Категория одушевленности/неодушевленности в японском языке отражается в сочетаемости существительных с глаголами бытия и местоимениями. Выбор вопросительных местоимений и глаголов осуществляется согласно следующей таблице:

Перевод существительных: иэ – 'дом', кабура – 'репка', дзидзи: – 'дед', оба:сан – 'бабка', маго – 'внучка', дзутика – 'Жучка', нэко – 'кошка', нэдзуми – 'мышка'.

Ответы:

1.

(1) Там находится дом.

(2) Там находятся дом и репка.

(4) Там находятся Жучка, кошка и мышка.

(5) Там находится мышка.

2.

(1) кабура-но усиро-ни нани-га аримас ка?

асоко-ни нани-мо аримасэн.

(2а) кабура-но усиро-ни дарэ-га имас ка?

асоко-ни дзидзи:-то оба:сан-то маго-га имас.

(2б) кабура-но усиро-ни нани-га имас ка?

асоко-ни дзутика-то нэко-то нэдзуми-га имас.

Задача демонстрирует категорию одушевленности в японском языке. Первоначальный вариант задачи имел стандартную форму, однако идея обратиться к персонажам сказки сделала задачу интереснее и оригинальнее. Кроме того, удалось привлечь рисунок, что имеет несколько плюсов: 1) привлекательность, 2) возможность не давать в условии переводы всех японских предложений, а оставить это для задания; 3) возможность спросить перевод слова «дзутика» (пример 4); общему решению задачи не мешает перевод собака, однако более внимательный решающий поймет, что это заимствованное имя собственное Жучка.

Среди билингв выделяются задачи на соответствия родственных языков, в частности славянских. Такова следующая задача.

Задача № 4

(автор А.А.Зализняк)

Даны чешские слова и соответствующие им русские:

Чешские слова

Byt	– быт	bitva	– битва
Druh	– друг	trouba	– труба
Hlíst	– глист	bўvati	– бывать
Kvas	– квас	dávati	– давать
PláŠt’	– плащ	padati	– падать
Pout'	– путь	krouŽiti	– кружить
soud	– суд	lízati	– лизать
Štít	– щит	muČiti	– мучить
vid	– вид	mysliti	– мыслить
Žar	– жар

Переведите на чешский язык: чиж, зуб, бык, кусать.

Примечание. Знак ў означает долготу гласной (над буквой i он ставится вместо точки), знак ' – мягкость предшествующей согласной.

Решение задачи № 4

Поскольку в задании требуется перевести русские слова на чешский, попытаемся составить правила, обеспечивающие переход (на буквенном уровне) от русских слов, содержащихся в основном материале задачи, к чешским.

С согласными все просто: русским б, в, г, д, ж, з, к, л, м, п, р, с, т, ч соответствуют чешские b, v, h, d, ž, z, k, l, m, p, r, s, t, č; русскому щ соответствует št в начале слова (štít) и št' в конце слова (plášt); русскому конечному ть соответствует t в существительном (pout), но ti в инфинитивах глаголов.

С гласными сложнее: каждой русской гласной соответствует две чешских – краткая и долгая; при этом, однако, для чешского u в роли долгого варианта выступает не ú, а ou. Каково же правило их распределения?

Рассмотрим вначале столбец неодносложных слов. Замечаем, что долгие чешские гласные (и ou) встречаются только в первом слоге. Они представлены в словах: trouba, bývati, dávati, krouziti, lízati. В остальных словах этого столбца все гласные краткие: bitva, padati, muciti, mysliti. Чем же различаются их русские соответствия? Прочтем переводы первой и второй группы вслух, и сразу станет понятно: разница в ударении! Ср. труба, бывать, давать, кружить, лизать и битва, падать, мучить, мыслить. Таким образом, для слов второго столбца верно, что в чешском слове долгота появляется в некотором слоге тогда и только тогда, когда в соответствующем русском слове ударение падает на один слог правее. Грубо говоря, чешская долгота соответствует русской предударности.

К сожалению, ситуация в первом столбце указанному правилу не подчиняется. Здесь представлены только односложные словоформы (т.е. совершенно одинаковые в смысле ударения), между тем различаются, как и во втором столбце, с одной стороны, hlíst, plášt', pout', soud, štít (с долгими гласными), с другой – byt, druh, kvas, vid, žar (с краткими). В чем же причина этого различия в данном случае? Коль скоро в примерах второго столбца разгадка основана на обращении к русскому ударению, нельзя ли попытаться и здесь найти какие-то различия, связанные с ударением? Но тогда, конечно, необходимо как-то выйти за рамки односложных словоформ. Задача немедленно решается, как только мы попробуем, например, просклонять рассматриваемые слова. В первой группе мы видим в родительном падеже глиста, плаща, пути, суда, щита, а во второй – быта, друга, кваса, вида, жара.

Становится понятно, что здесь действует в сущности то же самое правило, что и для примеров из второго столбца. Только мы должны теперь дополнить его указанием о том, что у русских существительных с односложной основой для проверки должна использоваться словоформа с ненулевым окончанием (например, родительный падеж единственного числа).

Теперь мы уже можем выполнить задание: чиж – číž (ср. чижа); зуб – zub (ср. зуба); бык – býk (ср. быка); кусать – kousati (поскольку ударение здесь кусать).

В качестве «разных языков» в билингве могут быть представлены и разные формы одного языка: графическая и звуковая (отраженная в транскрипции).

Задача № 5

(автор В.М.Алпатов)

В японском языке наряду с иероглифами используются две слоговые азбуки: катакана и хирагана. Среди японских слов есть слова, которые обычно или всегда записываются хираганой. Каждому знаку катаканы соответствует знак хираганы и наоборот, но написание знаков почти всегда различно. Дано несколько японских слов в их обычном написании с транскрипцией и переводами:

– боирā (паровой котел)

– анта (ты)

– комбо (маленький джаз-оркестр)

– оримпикку (Олимпийские игры)

– аримасу (вежливая форма глагола «быть»)

– кōкасасу (Кавказ)

Определите, какие слова записаны катаканой, а какие – хираганой, если известно, что первое слово записано катаканой и что один знак является одинаковым в катакане и хирагане.

Примечание. Черточка над гласной обозначает долготу гласного звука.

Решение задачи № 5

Сопоставляя число знаков в каждом слове, записанном японской азбукой, и число звуков и слогов в этих словах, можно предположить, что японское письмо в основном слоговое. Первое слово начинается с того же знака, которым кончается третье – ; видимо, это знак для слога бо. Третье и шестое слова начинаются с одного знака и одного слога ко (в шестом слове с удлинением гласного). Значит, – ко; тогда остаточно получаем знак для м – . Долгота гласного встречается дважды и оба раза в соответствующем месте имеется знак, состоящий из одной горизонтальной черты. Отсюда видно, что японская азбука – не чисто слоговая: одним знаком пишется слог типа «согласный + гласный», но долгота гласного и первый из двух стоящих рядом согласных обозначены особо.

Знак для м повторяется в третьем и четвертом словах, знак для ри – в четвертом и пятом, для а – во втором и пятом. Можно определить на основе всего вышеуказанного значение каждого знака. Однако некоторые слоги могут писаться различно, что связано с различием азбук, например, су в двух последних словах. Выпишем номера слов, соединив чертами те, где есть общие знаки: 1 – 3 – 6 4 – 5 – 2. Слова 1, 3, 6 записаны одной азбукой, поскольку если какие-то из них отнести к разным азбукам, то в любом случае у них будет больше одного общего знака. Слог су в словах 5 и 6 пишется по-разному, значит, они пишутся разными азбуками. Труднее всего определить принадлежность слова 4. Единственная возможность выбора двух вариантов заключается в обращении к значению слов. Слова 1, 3, 6, а также 4 обозначают предметы или события, не исконные для Японии; их названия – международные слова. В то же время слова 2, 5 – вряд ли заимствования (местоимения и глагол «быть» обычно бывают в языках исконными). Отсюда предположим, что слово 4 пишется той же азбукой (катаканой), что 1, 3, 6. Катаканой пишутся заимствования, хираганой – другие слова. Это действительно верно для японского языка.

Другой массовый тип лингвистических задач – билингвы с перепутанными соответствиями. Преимущество обычных билингв в том, что в них можно представить более сложный языковой материал. Но билингвы с перепутанными соответствиями незаменимы, когда в основе задачи лежит очень простое, но неожиданное соотношение между языками, секрет которого был бы сразу раскрыт, если бы задача имела форму обычной билингвы. Рассмотрим примеры задач этого типа.

Задача № 6

(автор А.Н.Журинский)

Даны обозначения некоторых дат на языке суахили и их переводы на русский язык в перепутанном порядке:

tarehe tatu Disemba jumamosi

tarehe pili Aprili jumanne

tarehe nne Aprili jumanne

tarehe tano Oktoba jumapili

tarehe tano Oktoba jumatatu

tarehe tano Oktoba jumatano

5 октября, понедельник

5 октября, среда

5 октября, воскресенье

2 апреля, вторник

4 апреля, вторник

3 декабря, суббота

А. Найдите русский перевод для каждого суахилийского словосочетания.

Б. Переведите на суахили: 3 апреля, среда; 2 декабря, воскресенье.

Решение задачи № 6

Замечая, что названия дней недели производны от числительных, предполагаем, что 'понедельник' буквально передается на суахили как 'первый день', 'вторник' – как 'второй день' и т.д., однако это предположение позволяет выполнить задание удовлетворительным образом только для четырех словосочетаний из шести. Естественная нумерация дней возникает, если отсчет начинать не с понедельника, а с субботы, как в мусульманском календаре. При этом понедельник будет третьим днем недели, вторник – четвертым и т. д.

А. 3 декабря, суббота; 2 апреля, вторник; 4 апреля, вторник; 5 октября, воскресенье; 5 октября, понедельник; 5 октября, среда.

Б. tarehe tatu Aprili jumatano, tarehe pili Disemba jumapili.

Задача № 7

(автор М.Е.Алексеев)

Ниже даны грузинские слова в латинской транскрипции с переводами на русский язык (в перепутанном порядке):

tvali, caltvala, calpexa, sartuli, ertsartuliani, ertadgiliani, mravalsartuliani;

одноместный, одноэтажный, глаз, одноглазый, этаж, одноногий, многоэтажный.

Определите перевод каждого грузинского слова.

Решение задачи № 7

Легко находим основы sartuli 'этаж' (встречается трижды) и tval- 'глаз' (встречается дважды). Отсюда: mraval- 'много', ert-...-ani, cal-...-a 'одно-'. Различие между последними двумя основами можно определить при сравнении слов одноэтажный и одноглазый: во втором слове одно- указывает на ущербность, недостаток, в то время как в первом соответствующий элемент имеет чисто количественное значение. Таким образом: tvali – глаз, caltvala – одноглазый, calpexa – одноногий, sartuli – этаж, ertsartuliani – одноэтажный, ertadgiliani – одноместный, mravalsartuliani – многоэтажный.

В некоторых задачах тип обычной билингвы совмещается с билингвой с перепутанными соответствиями.

Задача № 8

(автор Я.Г.Тестелец)

Даны местоимения на старославянском языке и их переводы на русский язык: – где, – тогда, 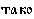– так.

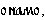
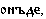
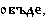
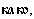
Дано также еще восемь местоимений на старославянском языке: Известно, что три из них переводятся как здесь, туда (далеко), сейчас.

Определите, каким именно местоимениям соответствуют три приведенных выше перевода, а также установите переводы остальных старославянских слов.

Решение задачи № 8

Легко догадаться, что местоимение 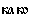имеет значение как, а 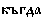– когда. Однако самое главное наблюдение, которое мы можем сделать, заключается в том, что каждое старославянское местоимение состоит из двух частей (скажем, корня и суффикса): 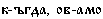и т.д. Попробуем составить таблицу:

Оказывается, что суффикс 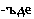означает место, суффикс 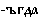– время, суффикс 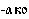– способ действия. Значение суффикса , которое нам пока неизвестно, можно установить: ведь одно из местоимений значит туда (далеко), и мы приходим к выводу, что этот суффикс означает направление. Таким образом, 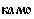– куда. Привлекая к решению два последних перевода – здесь и сейчас, устанавливаем значение местоимений с корнями 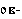и 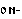: 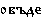значит здесь, – сейчас, – сюда, 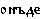– там (далеко), 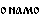– туда (далеко).

Особую разновидность представляют собой задачи, связанные с русским языком. Кроме данных, содержащихся в явном виде в условии, решающий может пользоваться информацией, которой он располагает как носитель языка. Эти задачи, как правило, затрагивают темы, не изучаемые в школе, привлекают внимание решающего к таким явлениям в родном языке, о которых ему не приходилось задумываться раньше. Но следует заметить, что даже те задачи, в которых предлагается анализировать материал совсем незнакомых языков, тоже позволяют глубже почувствовать русский язык (см. выше).

Задачи на русский язык затрагивают все уровни языка, интересны задачи на обнаружение следов древнего состояния в современном русском языке. Приводим пример задачи на словообразование.

Задача № 9

(автор И.Б.Иткин)

Даны русские прилагательные с суффиксами -н(ый), -н(ий), -шн(ый), -шн(ий): арбузный, барабанный, ватный, верхний, вечерний, винный, внешний, вчерашний, доминошный, задний, зряшный, карандашный, киношный, крайний, летний, медный, новогодний, нынешний, осенний, передний, послезавтрашний, тогдашний, хвойный, шоколадный, янтарный.

1. Сформулируйте правила употребления каждого из суффиксов.

2. Добавьте к этому списку слово соседний. Согласуется ли употребление суффикса -н(ий) в этом прилагательном с вашими правилами? Если нет, внесите в них необходимые уточнения.

3. Подумайте, от какого слова образовано прилагательное домашний?

4. Попробуйте определить, как раньше выглядело в русском языке слово там.

Решение задачи № 9

1. Разделим все имеющиеся в задаче прилагательные на четыре группы в зависимости от того, какой суффикс в них содержится. Сделать это легко: нужно только не забыть, что в слове карандашный выделяют не суффикс -шн(ый), а корень -карандаш- и суффикс -н(ый).

Прилагательные, разделенные на четыре группы

Прилагательные
на -н(ый)	на -н(ий)	на -шн(ий)	на -шн(ый)
арбузный винный медный шоколадный хвойный янтарный барабанный ватный карандашный	осенний новогодний вечерний задний летний крайний передний верхний	послезавтрашний внешний нынешний вчерашний тогдашний	доминошный киношный зряшный

В третьей и четвертой колонке в отличие от первой и второй суффиксы начинаются на -ш. Кроме того, во второй и третьей колонке согласный н в суффиксе мягкий, а в первой и четвертой – твердый. От чего же зависят эти различия?

По смыслу прилагательные третьей и четвертой групп явно не имеют между собой ничего общего; можно предположить, что согласный ш появляется в словах, образованных от определенных основ. Некоторые прилагательные на -шн(ый) и -шн(ий) образованы от наречий (послезавтра, вне, ныне, вчера, тогда, зря), а некоторые – от несклоняемых существительных (домино, кино). Эти два класса слов опять-таки никак не связаны между собой по смыслу, но их объединяет то, что и у одних, и у других существительных основа оканчивается на гласный. В то же время все прилагательные из двух первых колонок образованы от обычных склоняемых существительных (арбуз, вино, осень и т.д.), у которых основа оканчивается на согласный.

Напротив, у слов и словосочетаний, от которых образованы прилагательные из второй и третьей колонок, значения во многом сходны: все они обозначают либо пространство (например, край, верх, вне), либо время (например, Новый год, вечер, тогда). Для слов, от которых образованы прилагательные первой и четвертой групп, общее значение указать довольно сложно, но во всяком случае ни одно из них не обозначает ни пространство, ни время. Таким образом, правила употребления всех четырех суффиксов установлены.

2. Прилагательное соседний отличается от всех уже известных прилагательных с суффиксом -н(ий) тем, что слово сосед, от которого оно образовано, не обозначает ни пространства, ни времени. В то же время само слово соседний имеет пространственное значение: оно означает не 'принадлежащий соседу' – этот смысл в русском языке выражают с помощью прилагательного соседский, – а 'находящийся рядом, по соседству' (кстати, буквальное значение слова сосед – 'тот, кто сидит рядом'). Поэтому можно сказать, что суффиксы -н(ий) и -шн(ий) используются в относительных прилагательных с временным и пространственным значением, а суффиксы -н(ый) и -шн(ый) – в прилагательных, не имеющих такого значения.

3. То, что в прилагательном домашний есть суффикс -шн(ий), однозначно свидетельствует: оно образовано не от существительного дом, а от какого-то неизменяемого слова. Несложно догадаться, что таким словом может быть только наречие дома.

4. Установить, как раньше выглядело в русском языке слово там, очевидно, можно с помощью анализа образованного от него прилагательного тамошний. В этом слове выделите суффикс -шн(ий), который присоединяется к неизменяемым словам, оканчивающимся на гласный. При отбрасывании суффикса остается часть тамо-. Возможно, именно как тамо выглядело в прошлом наречие там.

Связь лингвистики с математикой отражают задачи на обозначение чисел в языках мира.

Задача № 10

(автор И.Н.Шахова)

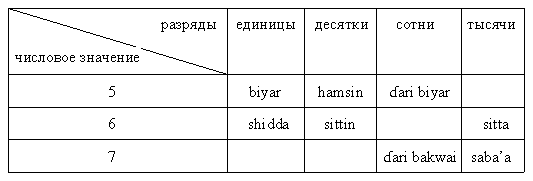
Даны числительные языка хауса:

А. Переведите с хауса: saba'in da biyar, shidda da sittin da shidda

Б. Запишите на хауса: 67, 5605.

Примечание. ', – особые согласные языка хауса.

Решение задачи № 10

Как и в русском языке, в языке хауса в названии числа сначала указываются бóльшие разряды, затем – меньшие: тысячи, сотни, десятки, единицы. Между числовыми значениями разрядов ставится слово «da».

Используя данные задачи, представим в таблице выражение числовых значений в разных разрядах:

Замечаем, что для обозначения сотен используется слово, обозначающее количество единиц, предваренное словом . Видимо, и значит '100'. Для обозначения одинакового количества единиц и десятков используются слова с разными корнями, а вот для десятков и тысяч используются те же корни. Это можно заметить, сравнивая sittin '60' и sitta '6000'. Для обозначения десятков используется суффикс -in (ср. также hamsin), тысяч – суффикс -а (saba'a).

Опираясь на подмеченные закономерности, выполняем задание.

A. 75, 666.

Б. sittin da bakwai, hamsa da shidda da biyar.

Среди самодостаточных лингвистических задач широко представлены и другие типы: задачи на дешифровку, на сравнительно-исторический анализ, на обнаружение правил построения определенных словосочетаний или выявление соотношений между словами и словосочетаниями. Многие задачи настолько оригинальны, что их трудно отнести к какому-то определенному типу. А количество и самих задач, и их типов продолжает увеличиваться.