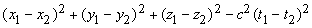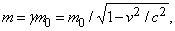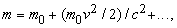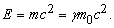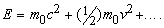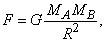ОТНОСИТЕЛЬНОСТЬ
ОТНОСИТЕЛЬНОСТЬ. Теории относительности образуют существенную часть теоретического базиса современной физики. Существуют две основные теории: частная (специальная) и общая. Обе были созданы А.Эйнштейном, частная – в 1905, общая – в 1915.
В современной физике частная теория относительности (ТО) вместе с квантовой механикой (которая в окончательном виде была сформулирована к 1925) играет такую же роль, какую раньше играла механика Ньютона. Ньютоновская механика хорошо описывала поведение объектов средних размеров, движущихся со скоростями, намного меньшими скорости света, но не могла описать движение очень малых объектов, таких, как атомы и входящие в состав атомов частицы или же частицы, из которых состоят космические лучи. Эти несоответствия стали проявляться в начале 20 в., и средства их преодоления оказались поистине революционными: квантовая механика, рассматривающая поведение очень малых частиц, отвергла ньютоновский детерминизм, а частная теория относительности, применимая к быстро движущимся телам, отвергла ньютоновское представление об абсолютном времени.
Ньютоновская механика по-прежнему применяется в практических расчетах и в тех разделах астрономии, где рассматриваемые объекты – планеты, самолеты, автомобили – достаточно велики и движутся со скоростью, намного меньшей скорости света. Но как частная ТО, так и квантовая механика очень важны для теоретического мышления физика, тем более что их правильность подтверждается многочисленными экспериментами. На этих теориях основывается почти вся современная ядерная физика. См. также АТОМ; МЕХАНИКА; КВАНТОВАЯ МЕХАНИКА.
В то же время общая теория относительности (ОТО), несмотря на ее огромное теоретическое значение, имеет довольно узкую область практического применения. Это в основном теория тяготения и инерции, заменяющая ньютоновскую теорию тяготения в точных расчетах очень больших систем (планетарного масштаба и более). Она позволяет в рамках физики и астрономии рассматривать структуру Вселенной как целого. ОТО включает в себя частную ТО как частный случай и потому пригодна для описания всех явлений, которые правильно описываются как теорией Ньютона, так и частной ТО. При этом все практические отличия ОТО связаны только с гравитационным полем.
Истоки возникновения теории относительности коренятся в противоречии между ньютоновской механикой и электромагнитной теорией Дж.Максвелла, выявившемся в конце 19 в. Созданию частной ТО, разрешающей это противоречие, мы обязаны не только Эйнштейну, но также Г.Лоренцу и А.Пуанкаре. Именно Лоренц и Пуанкаре создали математический аппарат частной ТО. Благодаря Эйнштейну, глубоко постигшему ее физический смысл, частная ТО получила быстрое и всеобщее признание. Среди более поздних исследователей, внесших существенный вклад в развитие частной ТО, следует упомянуть Г.Минковского (1864–1909). Минковский развил концепцию четырехмерного пространственно-временнóго континуума, в котором временнáя координата рассматривается как равноправная с пространственными координатами; он предложил также удобную геометрическую интерпретацию уравнений частной ТО.
Заслуга создания ОТО принадлежит исключительно Эйнштейну. Он ввел в физику новый математический аппарат – тензорное исчисление, разработанное Г.Риччи и Т.Леви-Чивитой. В математическом отношении теория оказалась весьма сложной, практических выводов из нее было мало, а проверить их путем наблюдений было трудно. В отличие от частной ТО, которая теперь почти полностью исследована, ОТО еще далека от этого. ОТО стала популярной не только среди физиков, но и в широких слоях образованных людей, когда наблюдения за затмением Солнца в 1919 подтвердили ее предсказание, согласно которому свет от далеких звезд, проходящий вблизи Солнца, должен испытывать отклонение.
На ОТО базировались многочисленные попытки создания единых теорий поля, охватывавших не только гравитационные, но также электромагнитные и прочие физические явления. Такие попытки, однако, имели мало успеха, а после смерти Эйнштейна, который и сам предпринял ряд таких попыток, активность в этом направлении снизилась. Физики, уверенные в возможности создания единых теорий, объясняющих все физические явления, полагают, что более перспективен синтез ОТО с квантовой теорией. Релятивистская квантовая теория, в некоторой мере объединившая частную ТО и квантовую теорию, добилась заметного успеха в подтверждении теории электрона П.Дирака (1928). И хотя разработка общей релятивистской квантовой теории еще далека от завершения, есть основание надеяться, что именно с ее развитием будут связаны дальнейшие успехи теоретической физики в целом.
ЧАСТНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Ньютоновская механика.
Данная статья написана так, что ее можно читать, не имея специальной математической подготовки. Необходимо лишь некоторое знание ньютоновской теории, имеющей с частной ТО ряд общих понятий. Начнем этот раздел с их рассмотрения.
Основные представления ньютоновской теории заключаются в следующем. Пространство и время рассматриваются как абсолютные и первичные. Абсолютное пространство однородно и изотропно. Это означает, что все его точки, как и все направления в нем, равноправны. Параллельные линии не сходятся и не расходятся, а это означает, что рассматривается евклидово пространство, свойства которого полностью описываются евклидовой геометрией.
На поведение тел влияет лишь их относительное расположение, а следовательно, их абсолютное расположение в пространстве не играет никакой роли. Любым подходящим твердым телом определяется «система отсчета», а положение и движение других тел описываются относительно системы координат, связанной с этим выбранным телом.
Если система отсчета покоится или находится в состоянии равномерного прямолинейного движения по отношению к абсолютному пространству, то она называется инерциальной, галилеевской или ньютоновской. В любой инерциальной системе отсчета законы механики имеют одну и ту же форму, в чем и выражается принцип относительности Галилея (галилеевская инвариантность). Согласно второму закону Ньютона, в любой инерциальной системе отсчета скорость изменения импульса любого тела пропорциональна приложенной к нему силе. Из принципа относительности Галилея следует, что путем одних лишь механических экспериментов невозможно установить, находится ли данное тело в состоянии покоя или равномерного прямолинейного движения по отношению к абсолютному пространству. Если же система отсчета движется ускоренно по отношению к абсолютному пространству, то для удовлетворения законов Ньютона нужно ввести фиктивные силы инерции, типичными примерами которых являются центробежная сила и сила Кориолиса.
«Абсолютное, истинное, математическое время само по себе и по самой своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно», – писал Ньютон в Математических началах натуральной философии (Philosophiae naturalis principia mathematica, 1687). Оно одно и то же в любой системе отсчета. Это очень важно, поскольку, как будет показано далее, время существенным образом входит в законы движения.
Пространственно-временне диаграммы.
Диаграммы хорошо дополняют уравнения при объяснении принципов теории относительности, равно как и ньютоновской механики. Более всего наглядны графики, показывающие, как положение объектов меняется со временем. Такие графики называются пространственно-временн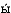
ми диаграммами.
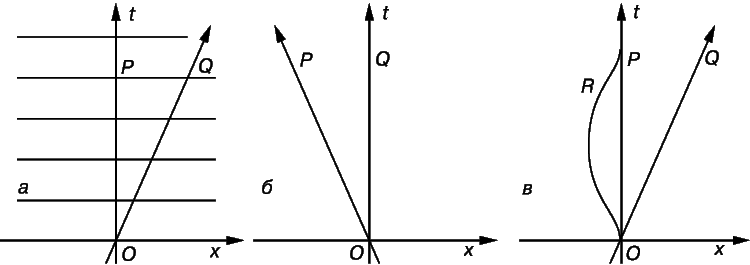
На рис. 1,а представлена ньютоновская пространственно-временнáя диаграмма, соответствующая равномерному и прямолинейному движению частицы Q вдоль оси х некоторой системы отсчета, в которой частица Р покоится. Координата х откладывается вправо, а время t – вверх. (Координаты y и z пока несущественны.) Диаграмма дает положение частицы Q в любой момент t. Наклонная линия, которая представляет историю частицы Q, называется мировой линией частицы. Любой момент в истории частицы Q, т.е. точка на мировой линии, называется мировой точкой или событием. Вертикальная ось – это мировая линия точки Р, которая находится в состоянии покоя. При t = 0 частица Q проходит мимо P. Можно сказать, что эта диаграмма вычерчена в системе отсчета, связанной с точкой Р. Тонкие горизонтальные линии являются линиями постоянного времени t (на которых время одинаково во всех точках). Они соединяют мировые точки, в которых события происходят одновременно. На рис. 1,б показана та же пара точек, но в системе отсчета, связанной с точкой Q. Теперь движется точка P, но влево от Q, поскольку ранее точка Q относительно P двигалась вправо. На рис. 1,в, как и на рис. 1,а, показаны точки P и Q и, кроме того, точка R, которая в начальный момент совпадает с Р, а затем уходит влево с нарастающей скоростью. Далее она замедляет движение и возвращается к Р. Изменения скорости характеризуются наклоном мировой линии относительно вертикали: чем больше скорость, тем больше изменение х при данном изменении t и тем больше наклон мировой линии.
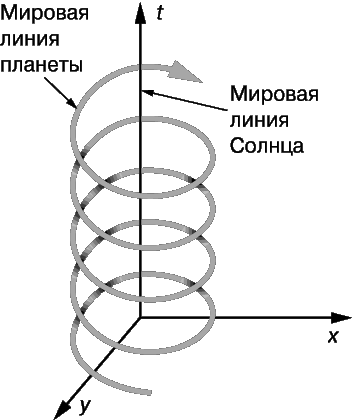
Наряду со временем на пространственно-временнóй диаграмме можно представить и две пространственные координаты; гораздо труднее – три. На рис. 2 показана мировая линия планеты (в двух пространственных координатах), движущейся вокруг Солнца. Ее орбита приблизительно круговая, и потому мировая линия имеет вид винтовой линии. Расстояние по вертикали между двумя ее соседними витками равно времени одного полного оборота планеты вокруг Солнца.
Распространение света.
Как уже отмечалось, частная ТО возникла в результате противоречия между ньютоновской механикой и максвелловской электромагнитной теорией света. Согласно теории Максвелла, свет представляет собой электромагнитные колебания, которые в виде волны распространяются с определенной скоростью. Скорость света в вакууме, обозначаемая буквой с, составляет 299 792 458 м/с. Скорость света в материальных средах меньше, чем в вакууме.
Во второй половине 19 в. было принято искать механические модели для всех физических явлений. Так, световые колебания рассматривались как колебания некоторой физической среды – «светоносного эфира». Предполагалось, что эфир неподвижен в абсолютном пространстве ньютоновской механики. Поэтому в принципе представлялось возможным в опытах со светом выявить движение Земли относительно эфира, т.е. ее абсолютное движение. При этом, если Земля движется в эфире со скоростью v, а свет – со скоростью с, то свет, движущийся в том же направлении, что и Земля, должен, согласно механике Ньютона, перемещаться относительно Земли со скоростью (с - v), а свет, движущийся в противоположном направлении, должен иметь относительно Земли скорость (с + v).
Стало быть, если с помощью закрепленного на Земле прибора удастся измерить скорость света в двух противоположных направлениях, то можно найти как (с - v), так и (с + v), а следовательно, и вычислить v, т.е. скорость Земли относительно эфира или, что то же самое, относительно абсолютного пространства. Такие измерения невозможно выполнить посредством чисто механических экспериментов, поскольку для них справедлив принцип относительности Галилея, но распространение света в светоносном эфире с этим принципом не связано.
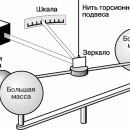
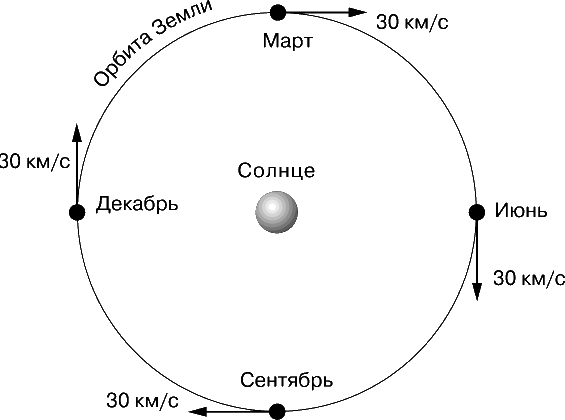
Первая попытка измерения скорости движения Земли относительно светоносного эфира была сделана А.Майкельсоном в 1881. Этот «эфирный» эксперимент он впоследствии с большей точностью повторил вместе с Э.Морли, а потому теперь эти эксперименты называются опытами Майкельсона – Морли. Опыт основан на сравнении скорости света в двух взаимно перпендикулярных направлениях. Подробности опыта мы рассматривать не будем, но его результат имеет огромнейшее значение. Он показал, что скорость Земли относительно эфира в любой момент не превышает 1 км/с. Однако, как известно, скорость Земли на орбите составляет около 30 км/с, а поскольку направление ее движения изменяется на противоположное каждые 6 мес, то ее скорость в любом заданном направлении должна изменяться на протяжении полугода примерно на 60 км/с (рис. 3). Поэтому был сделан вывод, что скорость света относительно прибора практически не зависит от движения прибора относительно эфира – результат, который совершенно не согласуется с механикой Ньютона. Затем была выполнена серия еще более точных опытов, и результат неизменно оставался отрицательным. См. также СВЕТ.
Это неожиданное открытие объяснялось по-разному. Предполагалось, что Земля должна каким-то образом увлекать за собой окружающий эфир. Однако гипотеза «увлекаемого эфира» противоречила некоторым астрономическим наблюдениям (таким, как звездная аберрация). Дж.Фитцджеральд (1851–1901) и независимо от него Г.Лоренц высказали предположение, что движение прибора (или любого другого предмета) в эфире должно вызывать сокращение его размеров на величину, необходимую для того, чтобы скомпенсировать ожидаемый эффект. Однако эта гипотеза о сокращении размеров, изначально базировавшаяся на ньютоновских представлениях, оказалась в противоречии с модифицированным опытом Майкельсона – Морли, выполненным в 1932 Р.Кеннеди и Э.Торндайком. В.Ритц выступил с утверждением, что скорость света в вакууме всегда должна быть равна с не относительно эфира, а относительно источника света, но это противоречило опытам Р.Томашека (выполненным с использованием солнечного света и света звезд в 1924 в духе опытов Майкельсона – Морли), а также астрономическим наблюдениям орбит двойных звезд.
Все разнообразие этих наблюдений можно свести к одному положению, с которым не согласуется ни одна из упомянутых гипотез: наблюдаемая скорость света, испускаемого движущимся в вакууме источником, не зависит от движения наблюдателя. Это положение явно противоречит ньютоновской механике.
Пространственно-временне диаграммы в частной ТО.
Противоречие было разрешено частной ТО, основные положения которой следуют из эмпирического заключения об инвариантности скорости света, принципа относительности Галилея и модифицированного второго закона Ньютона. Должны быть также модифицированы и уравнения преобразований Галилея.
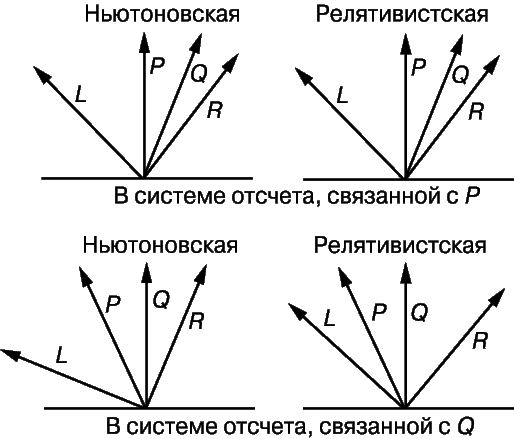
Чтобы согласовать утверждение об инвариантности скорости света с классическими преобразованиями Галилея, последние нужно изменить так, чтобы скорость света во всех инерциальных системах отсчета была одной и той же. Пространственно-временн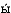е диаграммы, представленные на рис. 4, показывают, чтó из этого следует. На них мы видим мировые линии двух наблюдателей P и Q, с каждым из которых связана инерциальная система отсчета. На верхних диаграммах покоится Р, а Q движется вправо со скоростью v. В момент, когда Q проходит мимо Р, там вспыхивает лампа и световые лучи L и R расходятся влево и вправо со скоростью с. Поскольку скорости в обоих направлениях равны, лучи наклонены по отношению к вертикали одинаково. На нижних диаграммах представлен случай, когда путем надлежащего преобразования был осуществлен переход к другой инерциальной системе отсчета, где Q покоится, а Р движется влево со скоростью v. Левая диаграмма соответствует механике Ньютона: лампа наблюдателя Р теперь движется вместе с ним со скоростью v и, следовательно, световой луч L, распространяющийся влево, имеет скорость (c + v), тогда как луч R, распространяющийся вправо, имеет скорость (с - v). Это различие представлено разным наклоном лучей.
К сожалению, приведенное рассуждение противоречит требованию постоянства скорости света с в любой инерциальной системе отсчета. Представленная же справа диаграмма – релятивистская – соответствует случаю, когда это требование выполняется. В новой системе отсчета скорости обоих световых лучей равны с. Поэтому пространство-время должно быть подвергнуто таким преобразованиям, чтобы скорость света осталась неизменной. Этому условию удовлетворяют преобразования Лоренца.
Концепция пространства-времени.
То, каким образом пространственные координаты x, y, z и время t входят в уравнения преобразований Лоренца, навело Минковского на мысль, что пространство и время следует рассматривать не так, как в механике Ньютона с ее трехмерным евклидовым пространством и совершенно обособленной временнóй координатой, а всегда вместе, в виде некой четырехмерной комбинации. Новая концепция оказалась очень плодотворной и благодаря наглядной геометрической интерпретации во многом способствовала развитию теории. (Такое пространство-время часто называют пространством Минковского.) Вместо того чтобы рассматривать физическую систему как совокупность частиц в пространстве, ее следует представить как совокупность мировых линий частиц в пространстве-времени, которая описывает полную историю системы. Как и евклидово пространство в механике Ньютона, пространство-время Минковского однородно, изотропно и обладает дополнительными свойствами симметрии, вытекающими из преобразований Лоренца.
Главные следствия частной ТО.
Многие результаты частной ТО вытекают из преобразований Лоренца. Ниже приводятся лишь сами результаты, а не их вывод.
Относительность времени (относительность одновременности).
В теории относительности не существует абсолютного ньютоновского времени. В преобразованиях Галилея время остается без изменений. Из формул преобразований Лоренца следует, однако, что время в разных системах отсчета течет по-разному.
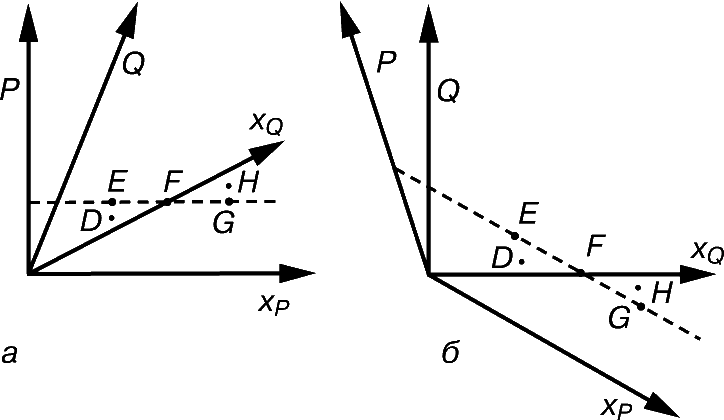
На рис. 5 представлены две пространственно-временн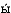е диаграммы. На обеих отображены одни и те же события, но одна соответствует системе отсчета, связанной с Р, а другая – системе, связанной с Q и движущейся относительно Р. Таким образом, они согласуются с релятивистскими диаграммами рис. 4 (справа), но здесь вместо одной оси х имеются две – для P и Q. Оси и мировые точки D, E, F, G и Н изображены так, что их положения на обеих диаграммах согласуются с преобразованиями Лоренца. На рис. 5,а, в системе, где Р покоится, мировые точки E, F и G лежат на горизонтальной линии, а это означает, что все три представленных события происходят в одно время в разных местах (одно и то же t, но разные х). Событие D наступает раньше других, а событие Н – позже. На рис. 5,б, в системе, где Q покоится, мировые точки, соответствовавшие в предыдущем случае одновременным событиям (при одном и том же значении t), теперь соответствуют событиям, происходящим при разных значениях tў. Рассмотрим диаграмму. События E, F и G более не являются одновременными: сначала произойдет G, затем F и, наконец, E. Событие D по-прежнему произойдет раньше Е, но позже F, хотя в предыдущем случае оно, как и следует из преобразований Лоренца, происходило раньше F. Аналогично ведут себя события H и G. Таким образом, относительна не только одновременность событий, но и порядок их наступления. Рассмотрим события D и E, а также события G и H. Каждая пара событий имеет на левой диаграмме одинаковую абсциссу х, указывающую на то, что пара событий происходила в одном и том же месте. Все эти события теперь будут происходить в разных местах (рис. 5,б). Конечно, то же самое происходит и в ньютоновской теории. Упорядоченность событий от прошлого к будущему нарушается в ТО далеко не всегда. Некоторые события имеют вполне определенный порядок, вне зависимости от используемой для их описания системы отсчета. Например, опыт показывает, что события на мировой линии некоторого наблюдателя должны происходить в определенном порядке, и два наблюдателя всегда согласятся по поводу порядка событий, при которых они оба присутствовали.
Рассмотрим это подробнее. Если (x1, y1, z1, t1) и (x2, y2, z2, t2) – пространственно-временн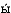е координаты двух событий, то выражение
не меняет своего вида при преобразованиях Лоренца и, следовательно, имеет одно и то же определенное значение независимо от того, в какой системе отсчета ведутся измерения. Если для некоторых двух событий это выражение равно нулю или отрицательно, то, как можно показать, события должны происходить в определенном порядке, одинаковом для всех систем отсчета. Если же это выражение положительно, то порядок событий зависит от системы отсчета: в различных системах одно или другое событие произойдет раньше, причем есть и такая система, в которой оба они произойдут одновременно.
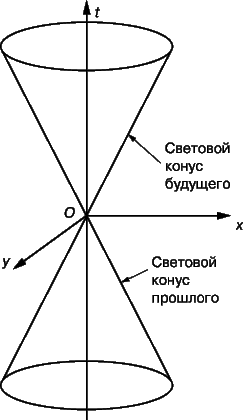
На рис. 6 представлена пространственно-временнáя диаграмма истории световой вспышки, произошедшей в мировой точке O в момент t = 0. Спустя время t свет распространится на расстояние ct во всех направлениях и будет находиться на поверхности сферы радиусом ct. История этой сферы на диаграмме имеет вид конуса с вершиной в точке O. Этот конус (верхний на рис. 6) называется конусом будущего. События, свет от которых достигнет точки O в момент t = 0, образуют конус прошлого (нижний конус на рис. 6). Он выглядит точно так же, как конус будущего, но обращен назад. Вместе конусы прошлого и будущего образуют двойной конус с вершиной в пространственно-временнóй точке O, называемый «световым конусом».
Любое событие, располагающееся внутри конуса будущего, всегда (во всех системах отсчета) происходит после события O. Поэтому событие O может, в принципе, быть его причиной. Любое событие, лежащее внутри конуса прошлого, всегда происходит до события O. Поэтому оно может, в принципе, быть причиной O. Любое событие, лежащее вне светового конуса, может происходить как до, так и после O, в зависимости от система отсчета. Поэтому между ним и событием O не может быть причинно-следственной связи. Сам световой конус не меняет формы при преобразованиях Лоренца, т.е. выглядит одинаково во всех системах отсчета, и это согласуется с опытным фактом, на котором основывается частная ТО, а именно, что скорость света в вакууме не зависит ни от движения источника, ни от движения наблюдателя.
Сокращение Фитцджеральда – Лоренца (лоренцево сокращение).
Из преобразований Лоренца сразу же следует, что измеренная длина движущегося объекта отличается от его длины, измеренной, когда он покоится.
Рассмотрим стержень, который покоится в некоторой системе отсчета, и пусть его длина, измеренная в этой системе, равна L. Если положение концов стержня измерить одновременно в системе отсчета, которая движется относительно первой со скоростью v (в направлении длины стержня), то выяснится, что расстояние между концами стержня равно уже не L, а L/g, где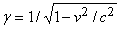 
, а c – скорость света. Таким образом, вследствие движения измеренная длина стержня сокращается в g раз. Величина g очень близка к единице, если скорость стержня мала по сравнению со скоростью света, и резко возрастает, когда его скорость приближается к c. Этим без всяких дополнительных гипотез о поведении объектов относительно абсолютного пространства или о свойствах эфира объясняется отрицательный результат опыта Майкельсона – Морли. Лоренцево сокращение объясняется только относительным движением объектов. То же относится и ко всем другим вопросам, рассматриваемым в рамках частной ТО.
Замедление времени.
Так называемое замедление времени или замедление хода движущихся часов, – явление, аналогичное рассмотренному выше сокращению длины. Оно состоит в изменении в g раз длительности измеряемых временных промежутков. Здесь есть два важных следствия, одно из которых имеет непосредственное приложение в физике.
Рассмотрим, как и прежде, двух наблюдателей P и Q и два события D и E, например в истории Q. Предположим, что в системе отсчета, где Q покоится (система Q), событие E происходит t секундами позже события D. Тогда в системе, где покоится P (система P), эти два события происходят в точках, разделенных расстоянием vg t, а E происходит после D не через t, а через g t секунд. Поскольку всегда g > 1, время между двумя событиями, измеренное в системе P, где события происходят в разных точках, всегда больше, чем в системе Q, где они происходят в одной точке. Скорость наблюдателя Q в системе P есть просто относительная скорость двух систем отсчета.
Релятивистское замедление времени было экспериментально подтверждено многими опытами, из которых наиболее наглядным является следующий. В космических лучах присутствуют мюоны – нестабильные элементарные частицы, которые можно также получить на ускорителе. Как показывают лабораторные эксперименты, спустя время t = 2Ч10–6 с после рождения эти частицы распадаются на электроны и нейтрино. Рождаются же мюоны в атмосфере из других космических частиц на высоте около 10 км и движутся к земле со скоростью v » 0,998 c, т.е. почти со скоростью света. Однако движущаяся с такой скоростью частица, согласно ньютоновской механике, может до своего распада пройти расстояние vt, равное всего 600 м. Следовательно, мюоны никак не могли бы достичь земной поверхности, если принять во внимание высоту, на которой эти частицы рождаются. Тем не менее они обнаруживаются на уровне моря. Объясняется это противоречие тем, что время жизни определялось в системе отсчета, где мюон покоится. В действительности же мюон движется относительно Земли с большой скоростью и вследствие релятивистского замедления времени интервал между событиями его рождения и распада различен для системы отсчета, в которой частица покоится, и системы, в которой она движется с большой скоростью. При переходе от системы покоя мюона к системе, в которой он движется со скоростью порядка 0,998 c, время жизни мюонов возрастает от t до g t, т.е. примерно в 16 раз. Измеренное лабораторными методами расстояние, проходимое мюонами от рождения до распада, составит vЧg t = 16Ч600 м, т.е. около 10 км. Этим и объясняется возможность наблюдения мюонов на уровне моря.
Парадокс часов.
В начальный период существования частной ТО большое внимание уделялось одному из ее следствий, так называемому парадоксу часов, или парадоксу близнецов, – пожалуй, наиболее поразительному из всех следствий этой теории. Кажущийся парадокс неразрешим, если оставаться на позициях механики Ньютона.
Рассматриваемое явление существенным образом связано с эффектом замедления времени, которое здесь приходится учитывать дважды. Пусть имеются часы 1, 2 и 3, расположенные следующим образом. Часы 1 находятся в покое относительно инерциальной системы отсчета S1. Со скоростью v относительно этой системы вправоравномерно движутся часы 2, с которыми связана другая инерциальная система отсчета S2. Часы 3 движутся равномерно влево со скоростью v относительно системы отсчета S1. С этими часами связана третья инерциальная система отсчета S3. Пространственно-временнáя диаграмма для данного случая представлена на рис. 7. События D, E и F таковы: D – часы 2 проходят мимо часов 1; E – часы 2 и 3 проходят друг мимо друга; F – часы 3 проходят мимо часов 1.
Если время между D и E, измеренное часами 2 в системе отсчета S2, где они покоятся, равно t, то вследствие замедления времени время между этими событиями, измеренное в S1, будет равно g t. Аналогично время между E и F, измеренное часами 3 в системе отсчета S3, где они покоятся, тоже равно t, а время между этими событиями, измеренное в S1, опять-таки должно быть равно g t. Таким образом, полное время между событиями D и F, измеренное часами 1 в системе S1,равно 2g t, а измеренное часами 2 в системе S2 и часами 3 в системе S3 – всего лишь 2t.
Чтобы лучше разобраться во всем этом, предположим, что часы 2 синхронированы с часами 1 и их показания совпадают в момент встречи (событие D), а часы 3 точно так же синхронированы с часами 2 для момента их встречи (событие E). Тогда часы 3 не покажут то же время, что и часы 1, в момент их встречи (событие F), а будут отставать на время 2g t - 2t или 2(g -1)t. Разница в показаниях часов 1 и 3 в момент события F может быть весьма значительной, если точки встречи достаточно удалены друг от друга.
Этот любопытный результат может показаться довольно абстрактным, пока в рассмотрение не входит человеческий фактор. Заменим часы 2 и 3 одними часами, помещенными на борту космического корабля, уносящего в звездные дали одного из близнецов, брат которого вместе с часами 1 остается на Земле. Пренебрежем на время орбитальным движением Земли и ускорениями космического корабля в моменты, когда он покидает Землю (D), поворачивает назад (E) и возвращается (F). Если, к примеру, корабль путешествует к ближайшей известной звезде Альфа Центавра, расстояние до которой составляет 4,2 светового года, а скорость корабля равна 99% скорости света, то от старта корабля до его возвращения на Землю пройдет около 8,5 года. Однако на самом корабле пройдет лишь 14,5 месяца. И если к началу путешествия близнецам было по 10 лет, то к его завершению землянину будет 18 с половиной, а его брату астронавту – чуть больше 11. При более длительных путешествиях разница возрастет. Этот вывод существенно не изменится, если учесть, что при взлете, повороте и посадке корабль должен разгоняться и тормозить постепенно, а не мгновенно, как в только что разобранном случае. Дело не в ускорениях, а в различии мировых линий близнецов: кривизна одной из них значительно больше, чем другой.
Казалось бы, приведенные рассуждения можно симметрично повторить, предполагая, что астронавт находится в покоящейся системе, а землянин – в движущейся. Тогда оказалось бы, что больше постареет астронавт – в этом и заключается парадокс. Однако это не так. Землянин (с часами 1) все время остается в покое в инерциальной системе отсчета S1, а астронавт (с часами 2 и 3) в процессе путешествия переходит от одной инерциальной системы к другой. Таким образом, близнецы находятся совсем не в симметричных положениях. Детальный анализ показывает, что движение землянина, с точки зрения астронавта, отличается от движения астронавта с точки зрения землянина. А поэтому и не получается, что при повторной встрече астронавт станет старше землянина, как это может показаться, если провести все рассуждения с точки зрения астронавта, считающего свою систему неподвижной. На заре теории относительности некоторые ученые пытались изобретать подобные парадоксы, выдвигая всегда качественные аргументы, основанные на интуитивных ньютоновских представлениях о времени. Количественный анализ должен приводить к правильному выводу, что близнец-астронавт при повторной встрече братьев окажется моложе. Результат этот однозначен и является прямым следствием пересмотра представлений о времени, которого требует частная ТО и необходимость которого подтверждается многими другими экспериментами. Полет к Альфе Центавра остается за гранью современных технических возможностей, однако эксперимент, подтверждающий эффект близнецов, все же был в 1971 проделан. Для этого были использованы очень точные атомные часы, установленные на борту самолета. Полеты осуществлялись вокруг Земли в восточном и западном направлениях, показания часов затем сверялись, и полученные результаты в обоих случаях были очень близки к предсказаниям теории относительности.
Релятивистская динамика.
Все описанные выше явления относятся к «релятивистской кинематике», т.е. могут быть выведены из преобразований Лоренца, которыми вместо преобразований Галилея связаны в частной ТО различные инерциальные системы отсчета. Но чтобы завершить переход к теории относительности, нужно найти замену второму закону Ньютона. Мы должны перейти к релятивистской динамике, рассматривающей влияние сил на движение тел. Новый закон движения должен удовлетворять следующим требованиям.
1. Его форма должна сохраняться при преобразованиях Лоренца, иначе возможны такие особые инерциальные системы отсчета, в которых закон имеет наиболее простой вид, что противоречило бы принципу равноправия инерциальных систем отсчета, на котором основана вся теория.
2. При скоростях, малых по сравнению со скоростью света, новый закон движения должен переходить во второй закон Ньютона, иначе возникло бы противоречие с опытными данными для движения с малыми скоростями, когда второй закон Ньютона выполняется.
Этих двух требований достаточно, чтобы более или менее однозначно установить новый закон движения.
Масса и энергия.
Различия между ньютоновскими и релятивистскими уравнениями движения проявляются и в различиях следствий, из них вытекающих. Когда эти различия экспериментально обнаруживаются, то оказывается, что они согласуются с релятивистскими уравнениями.
Первое, что нуждалось в подтверждении, – это зависимость массы от скорости. Частица, движущаяся с очень большой скоростью, согласно частной ТО, движется приблизительно так же, как и в ньютоновской механике, но ее масса должна следующим образом зависеть от скорости:
где m0 – масса частицы, измеренная в системе, в которой частица (пусть даже временно) покоится; масса m0 называется массой покоя или собственной массой. С этой квазиньютоновской точки зрения масса возрастает с увеличением скорости и стремится к бесконечности при приближении скорости частицы к скорости света. Это не парадокс, а лишь результат «ньютоновской» интерпретации релятивистского уравнения.
При малых скоростях, разлагая квадратный корень в ряд, получаем приближенно
где многоточием обозначены члены более высокого порядка малости, чем (v/c)2.
Изменение массы с изменением скорости впервые наблюдалось В. Кауфманом, а затем было подтверждено более точными опытами. Релятивистская зависимость массы от скорости подтверждается и экспериментами на ускорителях, которые проектируются с учетом этой зависимости и иначе не работали бы. См. также УСКОРИТЕЛЬ ЧАСТИЦ.
Еще одно важное следствие из релятивистской формулы – эквивалентность массы и энергии. Энергия E, входящая в релятивистский закон сохранения энергии, обычно записывается в виде массы m, умноженной на с2:
Это выражение можно разложить так же, как и выражение для массы:
Второй член совпадает с обычной формулой для ньютоновской кинетической энергии (многоточием обозначены члены, которые становятся существенными лишь при очень больших скоростях). Эти два равенства интерпретируются следующим образом: масса тела изменяется точно так же, как и энергия, заключенная в теле, причем выражение для энергии должно содержать постоянное слагаемое – так называемую энергию покоя m0c2, соответствующую массе покоя; при этом соотношение между массой и энергией имеет вид прямой пропорциональности с коэффициентом c2.
Из эквивалентности массы и энергии вытекает много следствий. Одно из наиболее впечатляющих – аннигиляция пары частиц и полное превращение их суммарной массы в излучение с соответствующей энергией. Такая аннигиляция наблюдается для пары электрон – позитрон (электрон заряжен отрицательно, а позитрон положительно) и для пары протон – антипротон. Эквивалентностью массы и энергии объясняется происхождение энергии звезд, она лежит в основе принципов получения атомной энергии и создания ядерного оружия, использующего деление и синтез ядер.
Так, энергия, излучаемая звездами, и энергия взрыва водородной бомбы имеют одинаковое происхождение. Четыре ядра водорода могут объединиться и образовать одно ядро гелия, причем масса ядра гелия будет меньше массы четырех ядер водорода, взятых порознь. Избыточная масса высвобождается в виде излучения, энергия которого связана с этой массой соотношением E = mc2. Большой энергетический выход таких источников энергии объясняется тем, что множитель c2 в этом уравнении очень велик – 9Ч1016 (м/с)2. Превращение водорода в гелий различными путями является основным источником звездной энергии, а также энергии, высвобождаемой при термоядерных взрывах. Энергия атомной (не водородной) бомбы и реакторов атомных электростанций обусловлена реакцией деления ядер: ядро урана или плутония расщепляется на две или более части, суммарная масса которых меньше массы исходного ядра, а избыток энергии выделяется частично в виде излучения, а частично в виде кинетической энергии продуктов деления. См. также ЯДЕР ДЕЛЕНИЕ; ЯДЕРНЫЙ СИНТЕЗ; АТОМНАЯ ЭНЕРГЕТИКА; НУКЛЕОСИНТЕЗ; ЯДЕРНОЕ ОРУЖИЕ.
Множество других приложений частной ТО практически во всех областях современной физики убедительно продемонстрировали ее правильность и превосходство над теорией Ньютона там, где предсказания этих двух теорий существенно различны. Далее мы перейдем к обобщению частной ТО, необходимому для адекватного рассмотрения явления тяготения.
ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Действие заданных сил описывается вторым законом движения Ньютона или соответствующими релятивистскими законами. Однако источники сил должны быть описаны дополнительными гипотезами. В теории Ньютона сила гравитации дается ньютоновским законом всемирного тяготения, согласно которому любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их гравитационных масс и обратно пропорциональной квадрату расстояния между ними.
Если гравитационные массы двух тел A и B равны MA и MB, а расстояние между ними R, то сила равна:
где G – ньютоновская гравитационная постоянная, равная 6,6726Ч10–11 м3/(кгЧс2).
Этот закон можно представить в иной форме, если ввести понятие поля сил: напряженность гравитационного поля, создаваемого телом A, в точке, находящейся на расстоянии R от него, равна силе, действующей на единичную пробную массу, помещенную в эту точку:
EA = GMA/R2.
Ньютон показал, что притяжение однородного сферического тела можно вычислять, принимая, что вся его масса сосредоточена в центре сферы. Поскольку Земля имеет приблизительно сферическую форму, напряженность создаваемого ею гравитационного поля на ее поверхности равна:
g = GMЗемли/(RЗемли)2 » 9,81 м/с2.
Это – просто ускорение силы тяжести, т.е. скорость увеличения скорости падающего тела.
Выражение для напряженности гравитационного поля, создаваемого телом А, характеризует его способность воздействовать с силой притяжения на другие тела. Сила же, действующая на любое другое тело, равна произведению напряженности поля EA на массу этого тела:
F = EAMB,
что согласуется с первым из приведенных выше выражений для силы притяжения между двумя телами. Из закона сохранения импульса следует, что все эти рассуждения остаются справедливыми, если два тела поменять местами. Таким образом, напряженность гравитационного поля, создаваемого телом B, равна EB = GMB/R2, а сила, действующая на тело A со стороны тела В, равна F = EBMA. Поведение системы из нескольких тел можно объяснить, рассмотрев силы, действующие на каждое тело со стороны всех других.
С современной точки зрения закон всемирного тяготения Ньютона имеет два недостатка, один очевидный, другой – более тонкий. Очевидный недостаток состоит в том, что закон неинвариантен относительно преобразований Лоренца и, следовательно, противоречит частной ТО. Сила, которую дает закон Ньютона в каждый конкретный момент времени, определяется расстоянием между телами, существующими в этот момент времени. Но мы уже видели, что расстояние между двумя телами в данный момент зависит от системы отсчета, в которой проводятся измерения, как и сам «данный момент».
Можно, конечно, модифицировать закон всемирного тяготения таким образом, чтобы он согласовался с частной ТО. И ряд подобных модификаций был предложен вскоре после создания частной ТО. Однако все они, как и теория Ньютона, страдали другим, более тонким недостатком, избавиться от которого удалось лишь в общей теории относительности (ОТО). Эти модификации представляют сейчас лишь исторический интерес и рассматриваться здесь не будут, а об упомянутом недостатке и предложенном Эйнштейном средстве избавления от него будет сказано в следующем разделе.
Гравитационная и инертная массы.
Понятие массы выступало выше в двух разных аспектах. В законах движения, ньютоновских и релятивистских, которые описывают действие заданных сил, масса характеризует сопротивляемость тела – его инерцию – по отношению к силам, стремящимся изменить его движение. В этом случае массу называют инертной. В ньютоновском же законе всемирного тяготения масса выступает как фактор, определяющий гравитационные силы, вызываемые данными телами, и здесь масса называется гравитационной. И нет оснований заранее предполагать, что эти массы связаны между собой. Иногда, чтобы подчеркнуть различие между ними, гравитационную массу даже называют гравитационным зарядом. Имеются, однако, очень точные экспериментальные данные, свидетельствующие о том, что обе массы пропорциональны друг другу, причем коэффициент пропорциональности для всех известных веществ один и тот же (подбором удобной системы единиц он может быть сделан равным 1).
Одним из таких свидетельств, известным, по крайней мере, еще со времен Галилея, является факт одинаково быстрого падения всех тел (если пренебречь сопротивлением воздуха). Большой свинцовый груз сильнее притягивается Землей, чем маленький грузик, и все же он не падает с бóльшим ускорением, поскольку бóльшая сила компенсируется и бóльшей инерцией. Опять-таки свинцовый и стальной грузики, уравновешенные на весах и, следовательно, имеющие равные гравитационные массы, падают с одинаковым ускорением и потому имеют также равные инертные массы.
Пусть ma, mb – инертные, а MA, MB – гравитационные массы тел A и B. Обозначим FA и FB гравитационные силы, действующие на эти тела со стороны Земли и вызывающие движение с ускорениями aA и aB, и примем, что, как и прежде, g = GMЗемли/(RЗемли)2. Из закона движения получаем
FA = mAaA; FB = mBaB,
а из закона всемирного тяготения –
FA = gMA; FB = gMB.
Наблюдения показывают, что все тела падают с одинаковым ускорением, т.е. aA = aB. Поэтому, приравнивая попарно выражения для FA и FB, получаем
mA/MA = mB/MB,
что и требовалось, а именно: отношение гравитационной массы к инертной одинаково для различных тел. Впервые точные измерения, подтвердившие пропорциональность гравитационной и инертной масс, были выполнены Р.Этвешем с сотрудниками в начале 20 в. Спустя 70 лет Р.Дикке в Принстоне и В.Б.Брагинский в Москве еще больше повысили точность таких измерений. Весы, к которым подвешивались грузы из различных материалов, были столь чувствительны, что если бы отношение гравитационной массы к инертной для этих материалов было неодинаковым, то из-за гравитационного воздействия Солнца был бы зарегистрирован эффект, изменяющийся на протяжении суток в соответствии с вращением Земли вокруг своей оси. Но в пределах погрешности порядка 1Ч10-12 такой эффект не был обнаружен.
Относительность инерции.
Другой общий недостаток механики Ньютона, выявленный в 19 в., – в значительной мере благодаря Э.Маху (1838–1916) – связан с тем, что она базируется на понятиях абсолютного пространства и абсолютного времени. Основная трудность, к которой это приводило, состояла в том, что нет никаких экспериментальных методов идентификации ни пространства, ни времени. Все мыслимые измерения – это измерения относительных положений, движений и отрезков времени. Почему бы, спрашивал Мах, вместо равномерного движения относительно абсолютного пространства в качестве критерия инерциальной системы отсчета не рассматривать равномерное движение относительно удаленных звезд? Мах пытался изменить ньютоновскую механику таким образом, чтобы согласовать ее с такими соображениями, однако столкнулся с трудностями, проистекающими главным образом из-за того, что его модификации не были достаточно революционными. Частная ТО не отвечала требованиям Маха – она всего лишь объединила абсолютное пространство и абсолютное время в абсолютное пространство-время, против которого можно было бы выдвинуть те же возражения, что и против абсолютного пространства и времени по отдельности.
Мысль Маха о желательных изменениях в механике можно кратко выразить в «принципе относительности инерции», который Эйнштейн, находившийся под сильным влиянием Маха, сформулировал в следующем виде: не может быть инерции относительно пространства; есть лишь инерция масс друг относительно друга. Анализ этого положения привел Эйнштейна к выводу, что с учетом гравитационного поля можно рассматривать как относительное не только равномерное движение, но и движение ускоренное. Это означает, что галилеевская инвариантность предъявляет слишком жесткие требования к эквивалентным системам отсчета. Эйнштейн выдвинул положение, что «законы физики должны быть применимы в системах отсчета, движущихся как угодно». Исходя из этого, он сформулировал принцип эквивалентности, согласно которому силы гравитации и силы инерции невозможно различить по результатам локальных механических опытов. На этой основе он предложил новую теорию, в которой пропорциональность гравитационной и инертной масс оказывалась необходимым следствием, а не случайностью, как в механике Ньютона. Что же касается маховской критики представлений об абсолютном пространстве и абсолютном времени, то она учитывалась введением положения, что свойства пространства-времени должны вытекать из распределения вещества, а не быть независимыми от него.
Принцип эквивалентности.
Ньютоновский закон движения и соответствующий релятивистский закон выполняются только в инерциальных системах отсчета. Если же измерения проводятся относительно некоторой другой системы, то в закон необходимо ввести новые слагаемые, чтобы учесть ускоренное движение. Так, в системе отсчета, вращающейся относительно инерциальной, дополнительные слагаемые представляют собой центробежную и кориолисову силы инерции. Указанные дополнительные члены содержат в качестве множителя инертную массу. Эти силы называют силами инерции, а вследствие эквивалентности инертной и гравитационной масс они входят в закон движения наравне с гравитационными силами. Это заключение, важность которого Эйнштейн понял за несколько лет до того, как сформулировал ОТО, есть одно из выражений принципа эквивалентности.
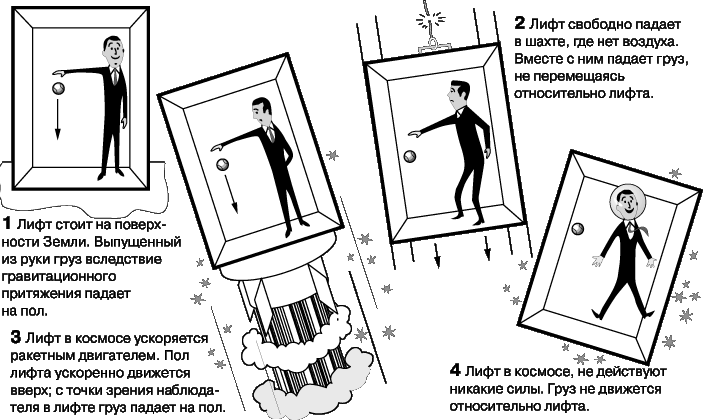
Эйнштейн проиллюстрировал данный принцип знаменитым мысленным экспериментом в лифте. (Осуществить такой эксперимент было бы технически сложно, но он помогает понять суть теории.) Этот эксперимент проводит ученый, который, находясь в лифте, выполняет четыре опыта (рис. 8):
1. Лифт стоит на поверхности Земли. Ученый в лифте выпускает из руки груз и видит, что он с ускорением падает на пол.
2. Лифт свободно падает в лифтной шахте (из которой откачан воздух для устранения его сопротивления). Ученый снова выпускает из рук груз, но, поскольку теперь и лифт, и груз находятся в состоянии свободного падения, груз «зависает» где-то между полом и потолком лифта (силами притяжения груза к лифту и телу ученого можно пренебречь).
Следующие два опыта выполняются в космическом пространстве, далеко от Земли, где всеми гравитационными полями можно пренебречь.
3. Лифт ускоряется вверх в вертикальном направлении с прикрепленным к нему ракетным двигателем. Если ускорение лифта равно 9,8 м/с2, то, когда ученый выпускает груз, он обнаруживает, что груз падает с таким же ускорением, как и в первом опыте. В отсутствие сил груз не должен приобретать ускорения, но благодаря ускоренному движению лифта ученый видит, что груз с ускорением падает вниз.
4. Лифт находится в космосе без ускорения, но по-прежнему далеко от Земли. Поскольку заметные гравитационные поля отсутствуют, когда ученый выпускает из рук второй груз, последний «зависает», как это было во втором опыте.
Мы можем представить результаты опытов в виде табл. 1. Результаты одинаковы, с одной стороны, для случаев, когда лифт неподвижен относительно Земли (в гравитационном поле Земли) и когда он находится в космосе и движется ускоренно вверх (опыты 1 и 3), а – с другой, когда лифт свободно падает в гравитационном поле Земли или же когда он неподвижен в далеком космосе (опыты 2 и 4).
| Таблица 1. РЕЗУЛЬТАТЫ ОПЫТОВ ЭЙНШТЕЙНА В ЛИФТЕ | |||
| Опыт | Направление действия гравитационного поля | Направление ускорения лифта | Направление ускорения груза относительно лифта |
| 1 | Вниз | – | Вниз |
| 2 | Вниз | Вниз | – |
| 3 | – | Вверх | Вниз |
| 4 | – | – | – |
Как явствует из опытов, действие гравитационного поля точно такое же, как и сил инерции, обусловленных ускоренным движением лифта. Это и есть непосредственное выражение принципа эквивалентности.
Основные следствия ОТО.
Важно понять, что за небольшими исключениями эйнштейновская теория предсказывает те же явления гравитации, что и ньютоновская. Таким образом, все явления, хорошо описываемые ньютоновской теорией тяготения, столь же хорошо описываются ОТО. Кроме того, ОТО снимает возражения Маха против ньютоновских концепций абсолютных пространства и времени.
В то же время все предсказания частной ТО непосредственно могут быть получены из ОТО, поскольку ОТО включает в себя частную ТО как частный случай, когда гравитационным полем можно пренебречь. Все же некоторые выводы ОТО отличаются от предсказаний ньютоновской теории. Предсказываемые эффекты, в которых проявляется различие между обеими теориями, зачастую слишком малы, чтобы их можно было обнаружить существующими методами, но там, где эти различия все же обнаруживаются, чаша весов склоняется в пользу ОТО. Опишем теперь три классических опыта по проверке ОТО и соответствующие экспериментальные результаты.
Смещение перигелия орбиты.
Согласно законам Кеплера, планеты Солнечной системы движутся по эллипсам, в общем фокусе которых находится Солнце. Это не вполне соответствует ньютоновской теории. Планеты не только притягиваются Солнцем, но и притягиваются друг к другу, хотя и гораздо слабее, чем к Солнцу, поскольку их массы намного меньше массы Солнца. Но если учесть эти малые взаимные возмущения, то наблюдаемое движение планет вполне согласуется с предсказаниями ньютоновской теории, за исключением малых деталей. Наиболее известное и подробно исследованное расхождение между теорией и экспериментом – так называемое смещение перигелия Меркурия.
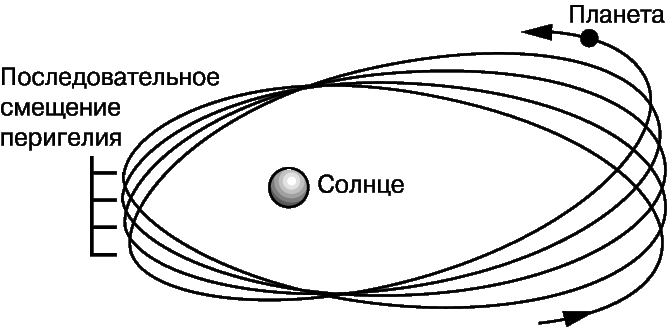
Перигелий – точка максимального приближения планеты к Солнцу. Из-за возмущающего действия других планет положение перигелия слегка изменяется при каждом орбитальном прохождении планеты через эту точку (рис. 9). Однако наблюдаемое смещение перигелия Меркурия, регистрируемое с начала 19 в., на 43 угловые секунды за сто лет больше предсказываемого ньютоновской теорией. Предлагались разные объяснения этого, в том числе гипотеза о существовании внутри орбиты Меркурия некой другой планеты (названной Вулканом) и модификация закона всемирного тяготения, но каждое из них приводило к новым противоречиям с данными астрономических наблюдений. Теория Эйнштейна объяснила смещение перигелия Меркурия без каких-либо дополнительных предположений. В случае других планет этот эффект оказывается слишком малым, и его пока не удается измерить.
Отклонение света.
Другим предсказанием ОТО является искривление светового луча или другого электромагнитного излучения при прохождении вблизи массивного объекта, например Солнца. Аналогичное отклонение следует и из ньютоновской теория тяготения, но ОТО предсказывает вдвое больший эффект. (В соответствии с ОТО луч должен отклоняться к объекту на расстояние, пропорциональное его массе и обратно пропорциональное минимальному расстоянию между ним и лучом.) Из этого следует, например, что если некий астроном, находящийся на Земле, фиксирует положение какой-нибудь звезды, находящейся практически на одной линии с Солнцем (так, что свет от звезды проходит в непосредственной близости от Солнца), и затем делает то же самое в другое время года, когда Солнце находится в другой части неба и когда его действием на свет от звезды можно пренебречь, то он обнаружит, что свет от одной и той же звезды пришел по двум слегка различающимся направлениям. Если Солнце наблюдается на фоне звезд, то те из них, которые ближе всего к Солнцу, должны обнаруживать наибольшее радиальное смещение от него относительно своего положения в отсутствие Солнца в данной части небосвода.
Однако наблюдение звезд, находящихся вблизи солнечного диска, затруднено, поскольку солнечный свет не позволяет их видеть. Такая возможность появляется во время полного солнечного затмения, когда звезды вблизи диска становятся видимыми на небе и их можно сфотографировать. Если через несколько месяцев сделать ночью новую фотографию, когда Солнце находится далеко, то можно сравнить два положения звезды. Различие, предсказываемое теорией, достаточно велико и составляет 1,74 угловой секунды для звезд, свет которых проходит вблизи солнечного диска. Такая величина без особых сложностей может быть зарегистрирована.
Первые наблюдения по проверке предсказаний Эйнштейна проводились в период полного затмения Солнца 29 мая 1919 двумя британскими экспедициями, одна из которых базировалась на о.Принсипи вблизи западного побережья Африки, а другая – в Бразилии. Результаты наблюдений подтвердили предсказания теории, а весть об этом успехе сделала с той поры имя Эйнштейна всемирно известным. На самом деле результаты измерений были не очень точными, и за последующие полвека состояние дел кардинально не улучшилось: наблюдения оставались чересчур сложными в техническом отношении.
Ситуация существенно изменилась с начала 1970-х годов благодаря появлению радиоинтерферометров с очень большой базой, в которых используются совместно работающие радиотелескопы, расположенные на разных континентах и отстоящие друг от друга на тысячи километров. Наблюдения в радиодиапазоне могут проводиться в любое время, а не только во время затмений. Совместно работающие радиотелескопы, расположенные далеко друг от друга, позволяют очень точно измерять направление на источник радиосигнала. Поскольку на протяжении года в пределах нескольких градусов от Солнца (при наблюдении с Земли) проходит целый ряд мощных квазизвездных источников радиоизлучения (квазаров), было проделано несколько тысяч измерений. Результаты подтверждают предсказания теории Эйнштейна в пределах погрешности 0,1ё0,2%, т.е. с точностью, в 100 раз более высокой, чем в прежних экспериментах по наблюдению звезд во время затмений.
Гравитационное красное смещение.
Еще одно следствие ОТО, на которое указал Эйнштейн, – зависимость наблюдаемой энергии фотона (частицы света) от его местоположения в гравитационном поле. Так как энергия пропорциональна частоте (по закону Планка E = hn), наблюдаемая частота тоже должна зависеть от местоположения. Так, например, фотон, соответствующий некоторой спектральной линии в спектре излучения какого-то атома на Солнце и впоследствии поглощенный на Земле, должен в момент прихода на Землю иметь частоту, на 1/400 000 меньшую, чем у такого же фотона, испущенного таким же атомом на Земле. В принципе это различие можно было бы обнаружить спектроскопическими методами, если бы не ряд мешающих факторов (таких, например, как доплеровское смещение частоты вследствие движения излучающего атома), которые пока что затрудняют однозначную интерпретацию результатов наблюдения за Солнцем.
В 1959 Р.Паунд с сотрудниками в Гарвардском университете провел эксперимент, основанный на возбуждении в земных условиях излучения некоторого атома с частотой, задаваемой с очень высокой точностью. Успеху эксперимента мешали трудности исключения неконтролируемого изменения частоты, обусловленного отдачей излучающего атома. Позднее задача была решена использованием излучающего атома, закрепленного в решетке некоторого кристалла: в этом случае отдачу принимает на себя весь кристалл, а потому она становится пренебрежимо малой.
В результате оказалось возможным регистрировать изменения в частоте излучения, «падающего» в гравитационном поле в пределах всего лишь 30 м. Результаты подтверждают предсказания Эйнштейна с точностью до 1%.
Задержка времени распространения света.
Еще одно поддающееся экспериментальной проверке следствие ОТО, связанное с отклонением света, было обнаружено только в 1964. Это замедление света в поле тяготения, впервые предсказанное И.Шапиро из Массачусетского технологического института (США). Шапиро указал на то, что вблизи большого тела, каким является Солнце, свет и радиосигнал должны не только отклоняться, но и распространяться с меньшей скоростью. Для сигнала, проходящего вблизи Солнца, время задержки может достигать 20 мкс, что легко обнаружить современными техническими средствами.
Шапиро с сотрудниками измерили время прохождения сигналов, отраженных от Меркурия и Венеры, а позднее провели более точные измерения с автоматическими межпланетными станциями серии «Викинг», которые совешили посадку на Марс, а также двигались по орбите вокруг Марса. Результаты измерений с помощью этих космических аппаратов подтвердили получение Шапиро предсказаний ОТО с точностью 0,1%.
Гравитационные волны.
Гравитационная волна – это колебания гравитационного поля, которые, подобно свету и другим электромагнитным волнам, могут переносить энергию. В теории Ньютона нет ничего подобного, но ОТО предсказывает существование гравитационных волн, распространяющихся со скоростью света.
Любое вращающееся несимметричное тело, а также система двух или более тел, движущихся одно относительно другого, должны излучать гравитационные волны. Однако из-за малости гравитационных сил по сравнению с электромагнитными, а отчасти из-за некоторых следствий технического характера, вытекающих из принципа эквивалентности, обнаружить гравитационные волны современными техническими средствами намного сложнее, чем электромагнитные. Существует, однако, убедительное косвенное подтверждение существования гравитационных волн, а также предсказаний ОТО, касающихся количества энергии, переносимой гравитационными волнами. Эти данные получены в процессе исследования знаменитого теперь астрономического объекта – двойного пульсара PSR 1913+16, открытого в 1975 Р.Халсом и Д.Тейлором в обсерватории Аресибо (Пуэрто-Рико).
Пульсар представляет собой быстро вращающуюся нейтронную звезду, генерирующую направленный пучок радиоволн, подобный лучу вращающегося прожектора. При регистрации их на Земле фиксируется импульсное излучение с периодом, равным периоду вращения нейтронной звезды. Двойной пульсар состоит из двух вращающихся вокруг общего центра масс звезд, при этом одна звезда – радиопульсар, а другая – либо тоже нейтронная звезда, либо белый карлик. Движение пульсара по его орбите может быть с большой точностью прослежено путем измерения времени прихода радиоимпульсов. Согласно ОТО, если система излучает гравитационные волны, то орбита пульсара должна немного изменяться. Регулярные наблюдения за пульсаром PSR 1913+16 убедительно показывают, что он излучает гравитационные волны с предсказываемой ОТО интенсивностью.
Множество отмеченных выше разнообразных экспериментов и наблюдений дает общей теории относительности ту основу, которой она не имела до 1960-х годов и благодаря которой тяготение теперь оказалось в главном русле современной физики.
Киттель Ч. и др. Механика. М., 1975
Вайскопф В. Физика в двадцатом столетии. М., 1977
Паули В. Теория относительности. М., 1983
Гамов Г. Приключения мистера Томпкинса. М., 1993
Ответь на вопросы викторины «Физика»