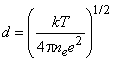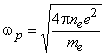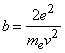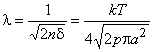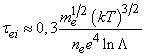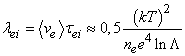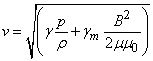ПЛАЗМА
ПЛАЗМА – частично или полностью ионизованный газ, образованный из нейтральных атомов (или молекул) и заряженных частиц (ионов и электронов). Важнейшей особенностью плазмы является ее квазинейтральность, это означает, что объемные плотности положительных и отрицательных заряженных частиц, из которых она образована, оказываются почти одинаковыми. Газ переходит в состояние плазмы, если некоторые из составляющих его атомов (молекул) по какой-либо причине лишились одного или нескольких электронов, т.е. превратились в положительные ионы. В некоторых случаях в плазме в результате «прилипания» электронов к нейтральным атомам могут возникать и отрицательные ионы. Если в газе не остается нейтральных частиц, плазма называется полностью ионизованной.
Между газом и плазмой нет резкой границы. Любое вещество, находящееся первоначально в твердом состоянии, по мере возрастания температуры начинает плавиться, а при дальнейшем нагревании испаряется, т.е. превращается в газ. Если это молекулярный газ (например, водород или азот), то с последующим повышением температуры происходит распад молекул газа на отдельные атомы (диссоциация). При еще более высокой температуре газ ионизуется, в нем появляются положительные ионы и свободные электроны. Свободно движущиеся электроны и ионы могут переносить электрический ток, поэтому одно из определений плазмы гласит: плазма – это проводящий газ. Нагревание вещества не является единственным способом получения плазмы.
Плазма – четвертое состояние вещества, она подчиняется газовым законам и во многих отношениях ведет себя как газ. Вместе с тем, поведение плазмы в ряде случаев, особенно при воздействии на нее электрических и магнитных полей, оказывается столь необычным, что о ней часто говорят как о новом четвертом состоянии вещества. В 1879 английский физик В.Крукс, изучавший электрический разряд в трубках с разреженным воздухом, писал: «Явления в откачанных трубках открывают для физической науки новый мир, в котором материя может существовать в четвертом состоянии». Древние философы считали, что основу мироздания составляют четыре стихии: земля, вода, воздух и огонь. В известном смысле это отвечает принятому ныне делению на агрегатные состояния вещества, причем четвертой стихии – огню и соответствует, очевидно, плазма.
Сам термин «плазма» применительно к квазинейтральному ионизованному газу был введен американскими физиками Лэнгмюром и Тонксом в 1923 при описании явлений в газовом разряде. До той поры слово «плазма» использовалось лишь физиологами и обозначало бесцветный жидкий компонент крови, молока или живых тканей, однако вскоре понятие «плазма» прочно вошло в международный физический словарь, получив самое широкое распространение.
Получение плазмы.
Способ создания плазмы путем обычного нагрева вещества – не самый распространенный. Чтобы получить термическим путем полную ионизацию плазмы большинства газов, нужно нагреть их до температур в десятки и даже сотни тысяч градусов. Только в парах щелочных металлов (таких, например, как калий, натрий или цезий) электрическую проводимость газа можно заметить уже при 2000–3000° С, это связано с тем, что в атомах одновалентных щелочных металлов электрон внешней оболочки гораздо слабее связан с ядром, чем в атомах других элементов периодической системы элементов (т.е. обладает более низкой энергией ионизации). В таких газах при указанных выше температурах число частиц, энергия которых выше порога ионизации, оказывается достаточным для создания слабоионизованной плазмы.
Общепринятым способом получения плазмы в лабораторных условиях и технике является использование электрического газового разряда. Газовый разряд представляет собой газовый промежуток, к которому приложена разность потенциалов. В промежутке образуются заряженные частицы, которые движутся в электрическом поле, т.е. создают ток. Для поддержания тока в плазме нужно, чтобы отрицательный электрод (катод) испускал в плазму электроны. Эмиссию электронов с катода можно обеспечивать различными способами, например нагреванием катода до достаточно высоких температур (термоэмиссия), либо облучением катода каким-либо коротковолновым излучением (рентгеновские лучи, g-излучение), способным выбивать электроны из металла (фотоэффект). Такой разряд, создаваемый внешними источниками, называется несамостоятельным.
К самостоятельным разрядам относятся искровой, дуговой и тлеющий разряды, которые принципиально отличаются друг от друга по способам образования электронов у катода или в межэлектродном промежутке. Искровой разряд обычно оказывается прерывистым даже при постоянном напряжении на электродах. При его развитии возникают тонкие искровые каналы (стримеры), пронизывающие разрядный промежуток между электродами и заполненные плазмой. Пример одного из наиболее мощных искровых разрядов являет собой молния.
В обычном дуговом разряде, который реализуется в довольно плотном газе и при достаточно высоком напряжении на электродах, термоэмиссия с катода возникает чаще всего от того, что катод разогревается падающими на него газовыми ионами. Дуговой разряд, возникающий в воздухе между двумя накаленными угольными стержнями, к которым было подведено соответствующее электрическое напряжение, впервые наблюдал в начале 19 в. русский ученый В.В.Петров. Ярко светящийся канал разряда принимает форму дуги благодаря действию архимедовых сил на сильно нагретый газ. Дуговой разряд возможен и между тугоплавкими металлическими электродами, с этим связаны многочисленные практические применения плазмы дугового разряда в мощных источниках света, в электродуговых печах для плавки высококачественных сталей, при электросварке металлов, а также в генераторах непрерывной плазменной струи – так называемых плазмотронах. Температура плазменной струи может достигать при этом 7000–10 000 К.
Различные формы холодного или тлеющего разряда создаются в разрядной трубке при низких давлениях и не очень высоких напряжениях. В этом случае катод испускает электроны по механизму так называемой автоэлектронной эмиссии, когда электрическое поле у поверхности катода просто вытягивает электроны из металла. Газоразрядная плазма, простирающаяся от катодного до анодного участков, а некотором расстоянии от катода образует положительный столб, отличающийся от остальных участков разряда относительным постоянством по длине характеризующих его параметров (например, напряженности электрического поля). Светящиеся рекламные трубки, лампы дневного света, покрытые изнутри люминофорами сложного состава, представляют собой многочисленные применения плазмы тлеющего разряда. Тлеющий разряд в плазме молекулярных газов (например, СО и СО2)широко используется для создания активной среды газовых лазеров на колебательно-вращательных переходах в молекулах.
Сам процесс ионизации в плазме газового разряда неразрывно связан с прохождением тока и носит характер ионизационной лавины. Это означает, что появившиеся в газовом промежутке электроны за время свободного пробега ускоряются электрическим полем и перед столкновением с очередным атомом набирают энергию, достаточную для того, чтобы ионизовать атом, т.е. выбить еще один электрон). Таким способом происходит размножение электронов в разряде и установление стационарного тока.
В тлеющих газовых разрядах низкого давления степень ионизации плазмы (т.е. отношение плотности заряженных частиц к общей плотности составляющих плазму частиц), как правило, мала. Такая плазма называется слабоионизованной. В установках управляемого термоядерного синтеза (УТС) используется высокотемпературная полностью ионизованная плазма изотопов водорода: дейтерия и трития. На первом этапе исследований по УТС плазма нагревалась до высоких температур порядка миллионов градусов самим электрическим током в так называемых самосжимаемых проводящих плазменных шнурах (омический нагрев) (см. ЯДЕРНЫЙ СИНТЕЗ). В тороидальных установках магнитного удержания плазмы типа токамак удается нагреть плазму до температур порядка десятков и даже сотен миллионов градусов с помощью впрыскивания (инжекции) в плазму высокоэнергетических пучков нейтральных атомов. Другой способ состоит в использовании мощного микроволнового излучения, частота которого равна ионной циклотронной частоте (т.е. частоте вращения ионов в магнитном поле) – то нагрев плазмы методом так называемого циклотронного резонанса.
Плазма в космосе.
В земных условиях из-за сравнительно низкой температуры и высокой плотности земного вещества естественная плазма встречается редко. В нижних слоях атмосферы Земли исключение составляют разве что разряды молнии. В верхних слоях атмосферы на высотах порядка сотен километров существует протяженный слой частично ионизованной плазмы, называемый ионосферой, который создается благодаря ультрафиолетовому излучению Солнца. Наличие ионосферы обеспечивает возможность дальней радиосвязи на коротких волнах, поскольку электромагнитные волны отражаются на определенной высоте от слоев ионосферной плазмы. При этом радиосигналы благодаря многократным отражениям от ионосферы и от поверхности Земли оказываются способными огибать выпуклую поверхность нашей планеты.
Во Вселенной основная масса вещества (ок. 99,9%) находится в состоянии плазмы. Солнце и звезды образованы из плазмы, ионизация которой вызывается высокой температурой. Так, например, во внутренней области Солнца, где происходят реакции термоядерного синтеза, температура составляет около 16 млн. градусов. Тонкая область поверхности Солнца толщиной порядка 1000 км, называемая фотосферой, с которой излучается основная часть солнечной энергии, образует плазму при температуре порядка 6000 К. В разреженных туманностях и межзвездном газе ионизация возникает под действием ультрафиолетового излучения звезд.
Над поверхностью Солнца находится разреженная сильно нагретая область (при температуре около одного миллиона градусов), которая носит название солнечной короны. Стационарный поток ядер атомов водорода (протонов), испускаемый солнечной короной, называется солнечным ветром. Потоки плазмы с поверхности Солнца создают межпланетную плазму. Электроны этой плазмы захватываются магнитным полем Земли и образуют вокруг нее (на расстоянии в несколько тысяч километров от поверхности Земли) радиационные пояса. Потоки плазмы, возникающие в результате мощных солнечных вспышек, изменяют состояние ионосферы. Быстрые электроны и протоны, попадая в атмосферу Земли, вызывают в северных широтах появление полярных сияний.
Свойства плазмы.
Квазинейтральность.
Одна из важных особенностей плазмы в том, что отрицательный заряд электронов в ней почти точно нейтрализует положительный заряд ионов. При любых воздействиях на нее плазма стремится сохранить свою квазинейтральность. Если в каком-то месте происходит случайное смещение (например, за счет флуктуации плотности) части электронов, создающее избыток электронов в одном месте и недостаток в другом, в плазме возникает сильное электрическое поле, которое препятствует разделению зарядов и быстро восстанавливает квазинейтральность. Порядок величины такого поля можно оценить следующим образом. Пусть в слое плазмы толщиной в Dx создается объемный заряд плотностью q. Согласно законам электростатики, на длине Dx он создает электрическое поле E = 4p qDx (использована абсолютная система единиц СГСЭ. В практических единицах – вольтах на сантиметр – это поле в 300 раз больше). Пусть в 1 см3 есть Dne лишних электронов сверх тех, которые точно нейтрализуют заряд ионов. Тогда плотность объемного заряда q = eDne , где e = 4,8·10–10 ед. СГС – заряд электрона. Электрическое поле, возникающее от разделения зарядов, равно
E = 1,8·10–6Dx в/см
В качестве конкретного примера можно рассмотреть плазму с такой же концентрацией частиц, как атмосферный воздух у поверхности Земли, – 2,7·1019 молекул/см3 или 5,4·1019 атомов/см3. Пусть в результате ионизации все атомы стали однозарядными ионами. Соответствующая концентрация электронов плазмы в этом случае равна ne = 5,4·1019 электрон/cм3. Пусть на длине 1 см концентрация электронов изменилась на 1%. Тогда Dne = 5,4·1017 электрон/см3, Dx = 1 см и в результате разделения зарядов возникает электрическое поле E » 1012 в/см.
Для создания такого сильного электрического поля понадобилась бы огромная энергия. Это говорит о том, что для рассматриваемого примера достаточно плотной плазмы фактическое разделение заряда будет ничтожно малым. Для типичного случая термоядерной плазмы (ne ~ 1012 – 1014 см–3 ) поле, которое препятствует разделению зарядов для рассмотренного выше примера, остается еще очень большим (E ~ 107109 в/см).
Длина и радиус Дебая.
Пространственный масштаб разделения заряда или ту характерную длину, ниже которой (по порядку величины) разделение зарядов становится заметным, можно оценить, вычисляя работу по разделению зарядов на расстояние d, которая совершается силами возникающего на длине x электрического поля E = 4pne ex.
С учетом того, что сила, действующая на электрон равна eE, работа этой силы равна 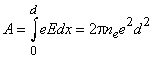
Эта работа не может превышать кинетическую энергию теплового движения частиц плазмы, которая для случая одномерного движения равна (1/2)kT, где k – постоянная Больцмана, T – температура, т.е.
A Ј (1/2)kT.
Из этого условия следует оценка максимального масштаба разделения заряда
Эта величина называется длиной Дебая по имени ученого, который ввел ее впервые, исследуя явление электролиза в растворах, где встречается аналогичная ситуация. Для рассмотренного выше примера плазмы при атмосферных условиях (ne = 5,4·1019 см–3Т = 273 К, k = 1,38·10–16 эрг/К) получаем d = 1,6 ·10–19 см, а для условий термоядерной плазмы (ne = 1014 см–3, T = 108K ) величина d = 7·10–3 см.
Для существенно более разреженной плазмы длина Дебая может оказаться больше размеров самого плазменного объема. В этом случае условие квазинейтральности нарушается, и такую систему уже нет смысла называть плазмой.
Длина d (или радиус Дебая ![]() ) является важнейшей характеристикой плазмы. В частности, электрическое поле, создаваемое каждой отдельной заряженной частицей в плазме, экранируется частицами противоположного знака и фактически исчезает на расстоянии порядка радиуса Дебая от самой частицы. С другой стороны, величина d определяет глубину проникновения внешнего электрического поля в плазму. Заметные отклонения от квазинейтральности могут происходить вблизи границ плазмы с твердой поверхностью как раз на расстояниях порядка длины Дебая.
) является важнейшей характеристикой плазмы. В частности, электрическое поле, создаваемое каждой отдельной заряженной частицей в плазме, экранируется частицами противоположного знака и фактически исчезает на расстоянии порядка радиуса Дебая от самой частицы. С другой стороны, величина d определяет глубину проникновения внешнего электрического поля в плазму. Заметные отклонения от квазинейтральности могут происходить вблизи границ плазмы с твердой поверхностью как раз на расстояниях порядка длины Дебая.
Плазменные колебания.
Еще одной важной характеристикой плазмы является плазменная (или лэнгмюровская) частота колебаний wp. Плазменные колебания – это колебания плотности заряда (например, электронной плотности). Они вызываются действием на заряд электрического поля, возникающего из-за нарушения квазинейтральности плазмы. Это поле стремится восстановить нарушенное равновесие. Возвращаясь в положение равновесия, заряд по инерции «проскакивает» это положение, что опять приводит к появлению сильного возвращающего поля.
Таким образом и возникают лэнгмюровские колебания плотности заряда в плазме. Электронная плазменная частота колебаний определяется при этом выражением
Для термоядерной плазмы, например, (ne = 1014 см–3 ) электронная плазменная частота оказывается равной wp = 1011c–1.
Идеальность плазмы.
По аналогии с обычным газом плазму считают идеальной, если кинетическая энергия движения составляющих ее частиц существенно больше энергии их взаимодействия. Заметное различие между плазмой и газом проявляется в характере взаимодействия частиц. Потенциал взаимодействия нейтральных атомов и молекул в обычном газе является короткодействующим. Частицы оказывают заметное влияние друг на друга лишь при непосредственном сближении на расстояния порядка диаметра молекул a. Среднее расстояние между частицами при плотности газа n определяется как n–1/3 (см. ГАЗ). Условие идеальности газа имеет при этом вид: a << n–1/3. Кулоновский потенциал взаимодействия заряженных частиц в плазме оказывается дальнодействующим, т.е. заряженные частицы создают вокруг себя протяженные электрические поля, медленно убывающие с расстоянием. Энергия кулоновского взаимодействия двух частиц с зарядом e, находящихся на расстоянии R друг от друга, равна e2/R . Подставляя вместо R среднее расстояние b между частицами и полагая среднюю кинетическую энергию частиц равной kT, условие идеальности плазмы можно представить в виде: ![]() << kT. Для оценки отклонения плазмы от идеальности обычно вводят параметр неидеальности плазмы
<< kT. Для оценки отклонения плазмы от идеальности обычно вводят параметр неидеальности плазмы
Очевидно, плазма является идеальной, если g << 1.
Условию идеальности плазмы можно придать более наглядный смысл, если ввести представление о так называемой сфере Дебая. В объеме плазмы выделяется шар с радиусом, равным радиусу Дебая, и подсчитывается число частиц ND, содержащихся в этом шаре,
Сравнение с критерием (3) показывает, что условие идеальности плазмы сводится к требованию, чтобы в сфере Дебая оказывалось достаточное число частиц (ND >> 1).
Для рассмотренных выше условий термоядерной плазмы (ne = 1014 см–3 , T = 108K ) получается, что ND » 108. Для плазмы, образующейся в разряде молнии (ne = 5·1019, T = 104), величина ND » 0,1. Такая плазма оказывается слабо неидеальной.
Термодинамика плазмы.
Если плазма удовлетворяет условию идеальности, то в термодинамическом отношении она ведет себя как идеальный газ, это означает, что ее поведение подчиняется обычным газовым законам (см. ГАЗ). Поскольку плазма представляет собой смесь частиц различных сортов (включая ионы и электроны), применение закона Дальтона позволяет записать уравнение состояния идеальной плазмы, которое связывает давление плазмы ![]() с плотностями каждого из видов частиц в смеси, в виде
с плотностями каждого из видов частиц в смеси, в виде
(5) p = p1 + p2 + … = (n1 + n2 + …) kT
Здесь T – общая для всех компонентов смеси температура, соответствующая установлению полного термодинамического равновесия в плазме. Реальная плазма многих экспериментальных установок, как правило, не находится в состоянии теплового равновесия. Так, газоразрядная плазма разогревается за счет энергии, которая выделяется при прохождении электрического тока в газе и передается, в основном, легкому компоненту плазмы – электронам. При столкновении с тяжелыми частицами (ионами и атомами) электроны отдают лишь незначительную часть своей энергии. Если электронов в плазме достаточно, чтобы обеспечить интенсивный обмен энергией между ними, в плазме устанавливается квазиравновесие, соответствующее установлению электронной температуры, отличающейся от температуры ионов и атомов. (Te > T). Такая плазма называется неизотермической. В газосветных рекламных трубках или в лампах дневного света, например, температура электронов обычно составляет десятки тысяч кельвинов, между тем как ионная температура и температура нейтрального газа оказываются не выше 1000–2000 К. Для полностью ионизованной плазмы термоядерных установок уравнение состояния плазмы записывается в виде
(6) p = k(neTe + niTi)
При этом, в отличие от обычной газоразрядной плазмы, температура ионов может оказаться заметно выше электронной.
Столкновения частиц в плазме.
В обычном газе процессы взаимодействия (столкновения) частиц носят, в основном, упругий характер. Это означает, что при таких столкновениях остаются неизменными суммарный импульс и энергия каждой взаимодействующей пары частиц. Если газ или плазма не сильно разрежены, столкновения частиц достаточно быстро приводят к установлению известного максвелловского распределения частиц по скоростям (см. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ), которое соответствует состоянию теплового равновесия. Плазма отличается от газа гораздо большим разнообразием процессов столкновений частиц. В слабоионизованной плазме особую роль играют упругие взаимодействия электронов с нейтральными атомами или молекулами, такие процессы, как, например, перезарядка ионов на атомах. По мере повышения степени ионизации плазмы к обычным упругим короткодействующим взаимодействиям нейтральных атомов и молекул и электронов с нейтральными частицами добавляются дальнодействующие кулоновские взаимодействия заряженных частиц плазмы. При достаточно высоких температурах или при наличии электронов с высокой энергией, которую они приобретают, например, в электрическом поле газового разряда, многие столкновения носят неупругий характер. К ним относятся такие процессы, как переход атомов и молекул в возбужденное состояние, ионизация атомов, рекомбинация электронов и ионов с участием третьей частицы и др.
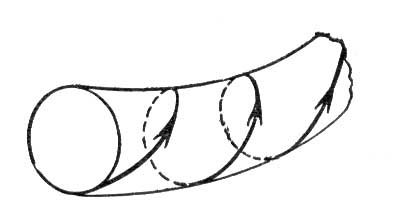
Особую роль в плазме играют кулоновские взаимодействия заряженных частиц. Если в нейтральном идеальном газе частицы большую часть времени находятся в свободном движении, резко меняя свою скорость лишь в моменты кратковременных столкновений, силы кулоновского притяжения или отталкивания между электронами и ионами сохраняют заметную величину даже при относительно большом удалении частиц друг от друга. Вместе с тем, это взаимодействие ограничено расстоянием порядка дебаевского радиуса, за пределами которого происходит экранирование взаимодействия выделенной заряженной частицы с другими заряженными частицами. Траекторию заряженных частиц уже нельзя представить в виде зигзагообразной линии, состоящей из коротких отрезков пути, как это делается при рассмотрении упругих столкновений в обычном газе. В плазме каждая заряженная частица все время находится в поле, создаваемом остальными электронами и ионами. Действие плазменного микрополя на частицы проявляется в плавном непрерывном изменении величины и направления скорости частицы (рис.1). Теоретический анализ показывает, что результирующий эффект слабых столкновений из-за их многочисленности оказывается при этом значительно большим, чем эффект, обусловленный редкими столкновениями, в результате которых происходит резкое изменение величины и направления скорости частицы.
При описании столкновений частиц важную роль играет так называемое сечение столкновений или сечение рассеяния. Для атомов, взаимодействующих как твердые упругие шарики, сечение s = 4p a2, где a – диаметр шарика. Можно показать, что в случае взаимодействий заряженных частиц кулоновское сечение столкновений состоит их двух множителей, учитывающих ближние и дальние взаимодействия. Ближнее взаимодействие отвечает крутому повороту в направлении движения частиц. Частицы сближаются до наименьшего расстояния между ними, если потенциальная энергия кулоновского взаимодействия сравнивается с кинетической энергией относительного движения частиц
где e1, e2 – заряды частиц, r – расстояние между ними, v – относительная скорость, m – приведенная масса (для электрона m равна массе электрона me). Для взаимодействия между электроном и однократно заряженным ионом расстояние ближнего взаимодействия b = rmin определяется как
Эффективное сечение взаимодействия есть площадь круга радиуса b, т.е. pb2. Однако направление движения частицы меняется и за счет дальних взаимодействий, приводящих к постепенному искривлению пути. Расчеты показывают, что полное сечение кулоновского рассеяния получается умножением сечения ближнего взаимодействия на так называемый кулоновский логарифм
(8) s = pb2s = pb2 ln L
Величина L, стоящая под знаком логарифма, равна отношению радиуса Дебая ![]() (формула (1)) к параметру ближнего взаимодействия b. Для обычной плазмы (например плазмы термоядерного синтеза) кулоновский логарифм меняется в пределах 10–20. Таким образом, дальние взаимодействия дают вклад в сечение рассеяния, больший на целый порядок величины, чем ближние.
(формула (1)) к параметру ближнего взаимодействия b. Для обычной плазмы (например плазмы термоядерного синтеза) кулоновский логарифм меняется в пределах 10–20. Таким образом, дальние взаимодействия дают вклад в сечение рассеяния, больший на целый порядок величины, чем ближние.
Средняя длина свободного пробега частиц между столкновениями в газе l определяется выражением.
Среднее время между столкновениями равно
где бvс = (8kT/pm)1/2 – средняя тепловая скорость частиц.
По аналогии с газом, можно ввести понятия средней длины свободного пробега и среднего времени между столкновениями и в случае кулоновских столкновений частиц в плазме, используя в качестве s выражение (8). Поскольку величина s в этом случае зависит от скорости частиц, для перехода к значениям, усредненным по максвелловскому распределению частиц по скоростям, можно приближенно использовать выражение для среднего квадрата скорости частиц бv2с = (3kT/me). В результате получается приближенная оценка для среднего времени электрон-ионных столкновений в плазме
что оказывается близким к точному значению. Средняя длина свободного пробега электронов в плазме между их столкновениями с ионами определяется как
Для электрон-электронных столкновений ![]() . Среднее время ион-ионных столкновений оказывается во много раз больше: tii = (2mi/me)1/2tei.
. Среднее время ион-ионных столкновений оказывается во много раз больше: tii = (2mi/me)1/2tei.
Таким образом, благодаря малой массе электрона в плазме устанавливается некоторая иерархия характерных времен столкновений. Анализ показывает, что приведенные выше времена соответствуют средним характерным временам передачи импульса частиц при их столкновениях. Как уже отмечалось ранее, при взаимодействии электрона с тяжелой частицей происходит очень малая (пропорциональная отношению их масс) передача энергии электрона. Благодаря этому характерное время передачи энергии ![]() оказывается в этой иерархии времен наименьшим:
оказывается в этой иерархии времен наименьшим:
tE = (mi/2me)tei.
Для условий термоядерной плазмы с ионами тяжелого изотопа водорода (дейтерия)
(ne = 1014 см–3, T = 108K, mD/me = 3,7·103) оценки дают
tei » 2·10–4c, tee » 3·10–4, tii » 10–2c, tE » 0,3c
Характерные средние длины свободного пробега для электронов и ионов при этих условиях оказываются близкими (~106 см), что во много раз превышает длины свободного пробега в газах при обычных условиях.
Среднее время обмена энергией между электронами и ионами может иметь при этом тот же порядок величины, что и обычное макроскопическое время, характерное для проводимых с плазмой экспериментов. Это означает, что в течение времени порядка величины tE , в плазме может поддерживаться устойчивая разность температур электронного и ионного компонентов плазмы.
Плазма в магнитном поле.
При высоких температурах и низких плотностях плазмы заряженные частицы большую часть времени проводят в свободном движении, слабо взаимодействуя друг с другом. Это позволяет во многих случаях рассматривать плазму как совокупность заряженных частиц, которые движутся почти независимо друг от друга во внешних электрических и магнитных полях.
Движение заряженной частицы с зарядом q во внешнем электрическом поле с напряженностью Е происходит под действием силы F = qE, что приводит к движению частицы с постоянным ускорением. Если заряженная частица движется со скоростью ![]() в магнитном поле, то магнитное поле действует на нее с силой Лоренца
в магнитном поле, то магнитное поле действует на нее с силой Лоренца
(13) F = qvB sin a,
где B – индукция магнитного поля в теслах (Tl) (в международной системе единиц СИ), a – угол между направлением линий магнитной индукции и направлением скорости частицы. При перемещении частицы параллельно линиям индукции (a = 0 или a = 180°) сила Лоренца равна нулю, т.е. магнитное поле не действует на движение частицы, и она сохраняет в этом направлении свою скорость. Наибольшая сила действует на заряженную частицу в перпендикулярном направлении (a = 90°), при этом сила Лоренца действует перпендикулярно как к направлению скорости частицы, так и направлению вектора магнитной индукции. Эта сила не совершает работу и поэтому может изменить лишь направление скорости, но не ее величину Можно показать, что траектория движения частицы представляет в этом случае окружность (рис.2). Радиус окружности легко найти, если записать для этого случая второй закон Ньютона, в соответствии с которым произведение массы на центростремительное ускорение равно силе, действующей на частицу,
(mv2/R) = qvB, откуда следует
Величина R называется ларморовским радиусом по имени английского физика Лармора, который еще в конце 19 в. изучал движение заряженных частиц в магнитном поле. Угловая скорость вращения частицы
wH = v/R определяется как
и носит название ларморовской (или циклотронной) вращения. Название это возникло потому, что именно с такой частотой обращаются заряженные частицы в специальных ускорителях – циклотронах.
Поскольку направление силы Лоренца зависит от знака заряда, электроны и положительные ионы вращаются в противоположные стороны, при этом ларморовский радиус однократно заряженных ионов в (M/m) раз больше радиуса вращения электронов (M – масса иона, m – масса электрона). Для ионов водорода (протонов), например, это отношение равно почти 2000.
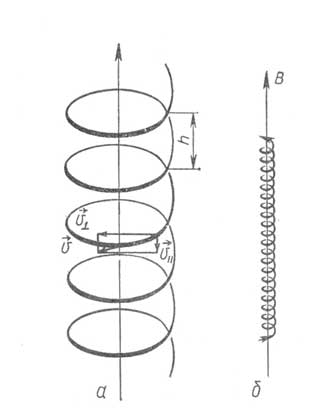
При равномерном движении заряженной частицы вдоль силовой линий магнитного поля и одновременном вращении вокруг нее траектория частицы представляет собой винтовую линию. Винтовые траектории иона и электрона изображены на рис.3.
В тех случаях, когда кроме магнитного поля на заряженную частицу действуют еще какие-нибудь поля (например, сила тяжести или электрическое поле) или когда магнитное поле неоднородно, характер движения частицы становится более сложным. Детальный анализ показывает, что в таких условиях центр ларморовского круга (его часто называют ведущим центром) начинает перемещаться в направлении, перпендикулярном магнитному полю. Такое движение ведущего центра называют дрейфом. Дрейфовое движение отличается от свободного движения заряженных частиц тем, что под действием постоянной силы оно происходит не равноускоренно, как это следует из второго закона Ньютона, а с постоянной скоростью. Из расчетов следует, что в случае однородного магнитного поля (такое поле получается, например, между плоскими полюсами большого электромагнита или внутри соленоида – равномерно намотанной длинной катушки с током) абсолютная величина скорости дрейфа определяется выражением
где F^ – составляющая силы, перпендикулярная силовым линиям магнитного поля. Такие силы, как сила тяжести и центробежная сила, которые в отсутствие магнитного поля действуют на все частицы одинаково (независимо от их заряда), заставляют электроны и ионы дрейфовать в противоположных направлениях, т.е. в этом случае возникает отличный от нуля дрейфовый электрический ток
В случае, когда наряду с однородным магнитным полем перпендикулярно его силовым линиям действует однородное электрическое поле, выражение для скорости дрейфа принимает вид:
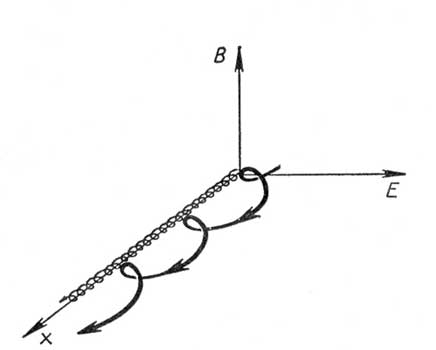
Сила электрического поля сама пропорциональна заряду частицы, поэтому в выражении (17) заряд сократился. Дрейф частиц в этом случае приводит лишь к движению всей плазмы, т.е. не возбуждает ток (рис.4). Дрейф, скорость которого определяется выражением (17), называется электрическим дрейфом.
Различные специфические виды дрейфа возникают в неоднородном магнитном поле. Так в результате искривления силовых линий (продольная неоднородность магнитного поля) на центр циклотронного круга действует центробежная сила, которая вызывает так называемый центробежный дрейф. Поперечная неоднородность поля (сгущение или разрежение силовых линий) приводит к тому, что циклотронный круг как бы выталкивается поперек поля с силой, пропорциональной изменению величины индукции магнитного поля на единицу длины. Эта сила вызывает так называемый градиентный дрейф.
Магнитное удержание плазмы.
Исследование особенностей поведения плазмы в магнитных полях вышло на первый план, когда встала проблема реализации управляемого термоядерного синтеза (УТС). Сущность проблемы заключается в том, чтобы осуществить на Земле те же реакции ядерного синтеза (превращение водорода в гелий), которые служат источниками энергии Солнца и других звезд. Сами эти реакции могут протекать лишь при сверхвысоких температурах (порядка сотен миллионов градусов), поэтому вещество в термоядерном реакторе представляет собой полностью ионизованную плазму. Очевидно, главная трудность состоит в том, чтобы изолировать эту высокотемпературную плазму от стенок реактора.
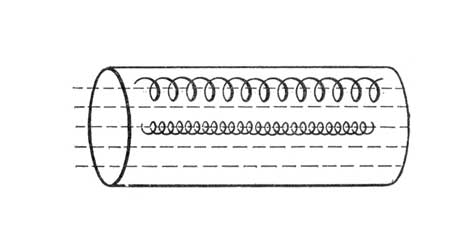
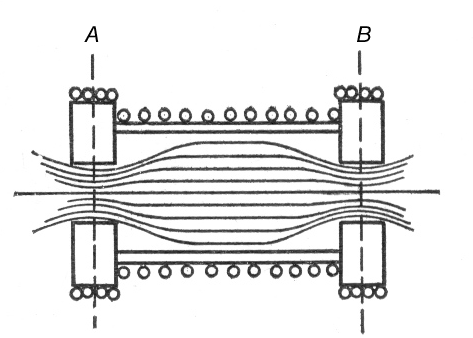
В 1950 советские физики И.Е.Тамм и А.Д.Сахаров и независимо от них ряд зарубежных ученых выдвинули идею магнитной термоизоляции плазмы. Эта идея может быть проиллюстрирована следующим простым примером. Если создать однородное магнитное поле внутри прямой трубы, заполненной плазмой, то заряженные частицы будут закручиваться вокруг силовых линий магнитного поля, перемещаясь только вдоль трубы (рис.5), чтобы избежать ухода частиц через концы трубы, можно соединить оба ее конца, т.е. согнуть трубу в «бублик». Труба такой формы представляет собой тор, а соответствующее устройство носит название тороидальной магнитной ловушки. Магнитное поле внутри тора создается с помощью намотанной на него проволочной катушки, по которой пропускается ток.
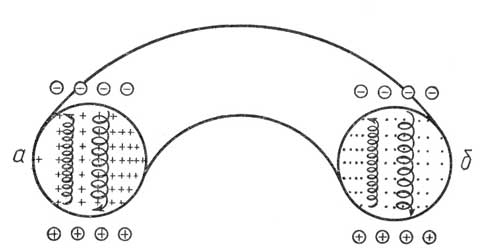
Однако, эта простая идея сразу наталкивается на ряд трудностей, которые связаны, в первую очередь, с дрейфовыми движениями плазмы. Поскольку силовые линии магнитного поля в тороидальной ловушке представляют собой окружности, можно ожидать центробежный дрейф частиц к стенкам ловушки. Кроме того, в силу принятой геометрии установки, витки с током располагаются на внутренней окружности тора ближе друг к другу, чем на внешней, поэтому индукция магнитного поля увеличивается по направлению от внешней стенки тора к внутренней, что очевидным образом приводит к градиентному дрейфу частиц к стенкам ловушки. Оба вида дрейфа частиц вызывают движение зарядов противоположного знака в разные стороны, в результате вверху образуется избыток отрицательных зарядов, а внизу – положительных. (рис.6). Это приводит к появлению электрического поля, которое перпендикулярно магнитному полю. Возникшее электрическое поле вызывает электрический дрейф частиц и плазма как целое устремляется к наружной стенке.
Идею магнитной термоизоляции плазмы в тороидальной ловушке можно спасти, если создать в ней магнитное поле специального типа, так чтобы линии магнитной индукции представляли собой не окружности, а винтовые линии, навивающиеся на тороидальную поверхность (рис.7). Такое магнитное поле можно создать либо с помощью специальной системы катушек, либо закручивая тор в фигуру, напоминающую цифру восемь («восьмерку»). Соответствующие устройства носят название стеллараторов (от слова «стеллар» – звездный). Другой способ, также позволяющий компенсировать дрейф плазмы в тороидальной ловушке, состоит в возбуждении вдоль тора электрического тока прямо по плазме. Систему с кольцевым током назвали токамак (от слов «токовая камера», «магнитные катушки»).
Существуют и другие идеи магнитного удержания плазмы. Одна из них заключается, например, в создании ловушек с магнитными «пробками» или так называемых «пробкотронов». В таких устройствах силовые линии продольного магнитного поля, сгущаются по направлению к торцам цилиндрической камеры, в которой находится плазма, напоминая своей формой горлышко бутылки (рис.8). Уходу заряженных частиц на стенки поперек продольного магнитного поля препятствует их закручивание вокруг силовых линий. Нарастание магнитного поля к торцам обеспечивает выталкивание циклотронных кружков в область более слабого поля, что и создает эффект магнитных «пробок». Магнитные «пробки» называют иногда магнитными зеркалами, от них, как от зеркала, отражаются заряженные частицы.
Диффузия плазмы поперек магнитного поля.
Предыдущий анализ поведения заряженных частиц в магнитном поле основывался на предположении об отсутствии столкновений частиц между собой. В действительности же частицы, конечно, взаимодействуют между собой, их столкновения приводят к тому, что они перескакивают с одной линии индукции на другую, т.е. перемещаются поперек силовых линии магнитного поля. Такое явление называют поперечной диффузией плазмы в магнитном поле. Анализ показывает, что скорость поперечной диффузии частиц уменьшается с увеличением магнитного поля (обратно пропорционально квадрату величины магнитной индукции B), а также с возрастанием температуры плазмы. Однако, на самом деле процесс диффузии в плазме оказывается более сложным.
Основную роль в поперечной диффузии плазмы играют столкновения электронов с ионами, при этом ионы, которые движутся вокруг силовых линий по окружностям большего радиуса, чем электроны, в результате столкновений «легче» переходят на другие силовые линии, т.е диффундируют поперек силовых линий быстрее, чем электроны. Из-за различной скорости диффузии частиц противоположного знака происходит разделение зарядов, которому препятствуют возникающие сильные электрические поля. Эти поля практически устраняют возникшую разницу в скоростях движения электронов и ионов, в результате чего наблюдается совместная диффузия разноименно заряженных частиц, которая называется амбиполярной диффузией. Такая диффузия поперек магнитного поля является также одной из важных причин ухода частиц на стенки в устройствах магнитного удержания плазмы.
Плазма как проводящая жидкость.
Если столкновения частиц в плазме играют значительную роль, рассмотрение ее на основе модели частиц, движущихся во внешних полях независимо друг от друга, становится не вполне оправданным. В этом случае более правильным является представление о плазме как сплошной среде, подобной жидкости. Отличие от жидкости состоит в сжимаемости плазмы, а также в том, что плазма является очень хорошим проводником электрического тока. Поскольку проводимость плазмы оказывается близкой к проводимости металлов, наличие токов в плазме приводит к сильному взаимодействию этих токов с магнитным полем. Движение плазмы, как проводящей жидкости, в электрическом и магнитном полях, изучается магнитной гидродинамикой.
В магнитной гидродинамике часто используют приближение идеально проводящей плазмы: это означает, что электрическое сопротивление плазмы считается очень малым (и, наоборот, проводимость плазмы – бесконечно большой). При движении плазмы относительно магнитного поля (или магнитного поля относительно плазмы) в плазме, в соответствии с законом электромагнитной индукции Фарадея, должна возникнуть ЭДС индукции. Но эта ЭДС вызывала бы в идеально проводящей плазме бесконечно большой ток, что невозможно. Отсюда следует, что магнитное поле не может перемещаться относительно такой плазмы: силовые линии поля оказываются как бы «вклеенными» или «вмороженными» в плазму, перемещаясь вместе с ней.
Понятие «вморожености» магнитного поля играет большую роль в физике плазмы, позволяя описать многие необычные явления, наблюдаемые особенно в космической плазме. Вместе с тем, если сопротивление плазмы не равно нулю, то магнитное поле может перемещаться относительно плазмы, т.е. происходит как бы «просачивание» или диффузия магнитного поля в плазму. Скорость такой диффузии тем больше, чем меньше проводимость плазмы.
Если рассмотреть неподвижный объем плазмы, окруженный внешним магнитным полем, то в случае идеально проводящей плазмы это поле не может проникнуть внутрь объема. Плазма как бы «выталкивает» магнитное поле за свои пределы. О таком свойстве плазмы говорят как о проявлении ее диамагнетизма. При конечной проводимости магнитное поле просачивается в плазму и первоначально резкая граница между внешним магнитным полем и полем в самой плазме начинает размываться.
Эти же явления можно просто объяснить, если ввести понятие о силах, действующих на плазму со стороны магнитного поля или об эквивалентной этим силам величине магнитного давления. Пусть проводник с током, расположен перпендикулярно силовым линиям магнитного поля. Согласно закону Ампера, на каждую единицу длины такого проводника со стороны магнитного поля с магнитной индукцией B действует сила равная IB , где I – сила тока в проводнике. В проводящей среде (плазме) можно выделить единичный элемент объема. Сила тока, протекающего перпендикулярно одной из граней этого объема, равна плотности тока в веществе j. Сила, действующая на единичный объем проводника в направлении, перпендикулярном силовым линиям магнитного поля, определяется тогда как F = j^B, где j^ – составляющая вектора плотности тока, направленная поперек магнитного поля. Примером может быть бесконечно длинный круговой цилиндр плазмы (плазменный шнур). Если плотность тока равна j, то легко убедиться, что на любую линию тока в плазменном цилиндре действует со стороны магнитного поля сила F, направленная к оси цилиндра, Совокупность этих сил стремится как бы сжать плазменный шнур. Полная сила, отнесенная к единице поверхности называется магнитным давлением. Величина этого давления определяется выражением
где m – магнитная проницаемость среды, m0 – магнитная постоянная (магнитная проницаемость вакуума). Пусть есть резкая граница между плазмой и вакуумом. В этом случае магнитное давление ![]() , действующее на поверхность плазмы извне, уравновешивается газокинетическим давлением плазмы p и давлением магнитного поля в самой плазме
, действующее на поверхность плазмы извне, уравновешивается газокинетическим давлением плазмы p и давлением магнитного поля в самой плазме
Из соотношения следует, что индукция магнитного поля B в плазме меньше индукции магнитного поля B0 вне плазмы, и это можно рассматривать как проявление диамагнетизма плазмы.
Магнитное давление играет, очевидно, роль некоторого поршня, сжимающего плазму. Для идеально проводящей среды (pm = 0) действие этого поршня обеспечивает равновесие между магнитным давлением, приложенным извне к плазме, и гидростатическим давлением внутри нее, т.е. удержание плазмы магнитным полем. Если проводимость плазмы конечна, то граница плазмы размывается, магнитный поршень оказывается «дырявым», спустя некоторое время магнитное поле полностью проникает в плазму и уже ничто не препятствует разлету плазмы под действием ее гидростатического давления.
Волны в плазме.
Если в обычном нейтральном газе в каком-то месте возникает разрежение или уплотнение среды, то оно распространяется внутри газа от точки к точке в виде так называемой звуковой волны. В плазме, помимо возмущения давления (или плотности) среды, возникают колебания за счет разделения зарядов (лэнгмюровские или плазменные колебания). Простейшим и важнейшим способом возбуждения плазменных колебаний является, например, возбуждение их пучком быстрых электронов, проходящим через плазму, который вызывает смещение электронов плазмы из положения равновесия. Под совместным действием сил давления и электрического поля плазменные колебания начинают распространяться в среде, возникают так называемые лэнгмюровские или плазменные волны.
Распространение периодических колебаний в среде характеризуется длиной волны l, которая связана с периодом колебаний T соотношением
l = vT, где v – фазовая скорость распространения волны. Наряду с длиной волны рассматривают волновое число k = 2p/l. Поскольку частота колебаний w и период T связаны условием wT = 2p, то
(19) w = kv
Направление распространения волны характеризуется волновым вектором, равным по модулю волновому числу. Если направление распространения волны совпадает с направлением колебаний, то волну называют продольной. Когда колебания происходят перпендикулярно направлению распространения волны, она называется поперечной. Звуковые и плазменные волны являются продольными. Примером поперечных волн являются электромагнитные волны, которые представляют собой распространение в среде периодических изменений напряженности электрического и магнитного полей. Электромагнитная волна распространяется в вакууме со скоростью света C.
Для обычных звуковых и электромагнитных волн, распространяющихся в нейтральном газе, скорость их распространения не зависит от частоты волны. Фазовая скорость звука в газе определяется выражением
Где p – давление, r – плотность, g = cp/cv – показатель адиабаты (cp и cv – удельные теплоемкости газа при постоянном давлении и при постоянном объеме соответственно)/
Для волн, распространяющихся в плазме, наоборот, характерно наличие этой зависимости, которая носит название закона дисперсии. Электронные плазменные волны распространяются, например, с фазовой скоростью
где w0, – частота электронных плазменных колебаний, ![]() – квадрат скорости электронного звука.
– квадрат скорости электронного звука.
Фазовая скорость электронных волн всегда больше скорости звуковых. Для больших длин волн фазовая скорость стремится к бесконечности – это значит, что весь объем плазмы колеблется с постоянной частотой w0.
Колебания ионов в плазме происходят с гораздо меньшей частотой из-за большой массы ионов по сравнению с электронами. Электроны, обладающие большей подвижностью, следуя за ионами, почти полностью компенсируют электрические поля, возникающие при таких колебаниях, поэтому распространение ионных волн происходит со скоростью ионного звука. Исследования показали, что ионно-звуковые волны в обычной равновесной плазме с температурой электронов Te, мало отличающейся от температуры ионов Ti, сильно затухают уже на расстояниях порядка длины волны. Однако практически незатухающие ионные волны существуют в сильно неизотермической плазме (Te>>Ti), при этом фазовая скорость волны определяется как v = (kTe/mi)1/2. Это соответствует так называемому ионному звуку с электронной температурой. В этом случае скорость ![]() заметно превышает тепловую скорость ионов vt ~ (kTi/mi)1/2.
заметно превышает тепловую скорость ионов vt ~ (kTi/mi)1/2.
Особый интерес представляет распространение электромагнитных волн в плазме. Закон дисперсии имеет в этом случае имеет вид
Распространение волны оказывается возможным только при условии, что частота волны w превышает электронную плазменную частоту w0. Если скорость электромагнитной волны в вакууме равна с (скорость света), то в веществе фазовая скорость распространения определяется формулой v = c/n, где n – показатель преломления среды. Из формул (19) и (21) следует
ри w < w0 показатель преломления становится мнимым, это и означает, что при таком условии волна в плазме не может распространяться. Если после прохождения какой-то среды электромагнитная волна попадает на границу плазмы, то она проникает лишь в тонкий поверхностный слой плазмы, так как при выполнении условия w < w0 колебания в электромагнитной волне являются «медленными». За период колебаний T заряженные частицы плазмы «успевают» распределиться таким образом, что возникающие в плазме поля препятствуют продвижению волны. В случае «быстрых» колебаний (w > w0) такое перераспределение не успевает произойти, и волна свободно распространяется по плазме.
В соответствии с формулой (2) электронная плазменная частота ![]() . Это позволяет для фиксированных значений ne находить предельное значение длины электромагнитной волны, выше которой она отражается от границы плазмы. Для оценки этой величины в случае прохождения электромагнитных волн в ионосфере Земли используется формула lпр = 2p(c/w0), где w0 определяется формулой (2). Максимальная концентрация электронов в ионосфере, согласно ракетным зондовым измерениям, равна 1012м–3 . Для плазменной частоты в этом случае получается значение w0 = 6·10–7с–1, а для длины волны lпр » 30 м. Следовательно, радиоволны с l > 30 м будут отражаться от ионосферы, а для дальней космической связи со спутниками и орбитальными станциями нужно использовать радиоволны со значительно меньшей длиной волны.
. Это позволяет для фиксированных значений ne находить предельное значение длины электромагнитной волны, выше которой она отражается от границы плазмы. Для оценки этой величины в случае прохождения электромагнитных волн в ионосфере Земли используется формула lпр = 2p(c/w0), где w0 определяется формулой (2). Максимальная концентрация электронов в ионосфере, согласно ракетным зондовым измерениям, равна 1012м–3 . Для плазменной частоты в этом случае получается значение w0 = 6·10–7с–1, а для длины волны lпр » 30 м. Следовательно, радиоволны с l > 30 м будут отражаться от ионосферы, а для дальней космической связи со спутниками и орбитальными станциями нужно использовать радиоволны со значительно меньшей длиной волны.
На использовании тех же теоретических выражений основывается важный метод диагностики плазмы – микроволновое зондирование. Плазму просвечивают направленным пучком электромагнитных волн. Если волна проходит через плазму и обнаруживается приемником, помещенным с другой стороны, то концентрация плазмы ниже предельной. «Запирание» сигнала означает, что концентрация плазмы выше предельной. Так, для обычно используемых в этом случае волн с длиной l = 3 см предельная электронная плотность составляет 1012 см–3 .
Картина распространения волн в плазме существенно усложняется при наличии внешнего магнитного поля. Только в том частном случае, когда направление электрических колебаний в волне происходит вдоль магнитного поля, электромагнитная волна в плазме ведет себя также как и в отсутствие магнитного поля. Наличие магнитного поля приводит к возможности распространения волн совершенно другого характера, чем в случае обычных электромагнитных волн. Такие волны возникают в том случае, когда направление электрических колебаний перпендикулярно внешнему магнитному полю. Если частота колебаний электрического поля мала по сравнению с циклотронными частотами в плазме, то плазма ведет себя просто как проводящая жидкость, и поведение ее описывается уравнениями магнитной гидродинамики. В этой области частот параллельно магнитному полю распространяются магнитогидродинамические волны, а перпендикулярно ему – магнито-звуковые. Физическую природу этих волн можно наглядно представить, воспользовавшись понятием вмороженного магнитного поля.
В магнито-звуковой волне вещество вместе с вмороженным в него полем перемещается вдоль направления распространения волны. Механизм явления аналогичен обычному звуку, только вместе с колебаниями давления (плотности) самой плазмы вдоль того же направления возникают сгущения и разрежения силовых линий вмороженного магнитного поля. Скорость распространения волны может быть найдена по обычной формуле для скорости звука, в которой дополнительно учтено наличие магнитного давления. В результате скорость волны
(Показатель адиабаты для магнитного давления gm = 2). Если отношение газового давления к магнитному мало, то
Механизм распространения волн в направлении, параллельном магнитному полю, можно сравнить с распространением волны вдоль колеблющейся струны. Скорость движения вещества здесь перпендикулярна направлению распространения. Силовые линии магнитного поля играют роль как бы упругих нитей (струн), и механизм колебаний здесь состоит в «изгибании» магнитных силовых линий вместе с «приклеенной» к ним плазмой. Несмотря на различие в механизмах явления (по сравнению с предыдущим случаем), скорость распространения магнитогидродинамических волн при низких частотах в точности равна скорости магнитного звука VA (24). Магнитогидродинамические волны были открыты шведским астрофизиком Альфвеном в 1943 и в его честь носят имя альфвеновских волн.
Владимир Жданов
Франк-Каменецкий Д.А. Плазма – четвертое состояние вещества. М., Атомиздат, 1963
Арцимович Л.А. Элементарная физика плазмы. М., Атомиздат, 1969
Смирнов Б.М. Введение в физику плазмы. М., Наука, 1975
Милантьев В.П., Темко С.В. Физика плазмы. М., Просвещение, 1983
Чен Ф. Введение в физику плазмы. М., Мир, 1987
Ответь на вопросы викторины «Физика»