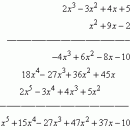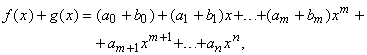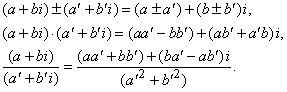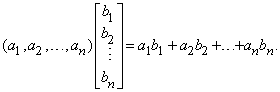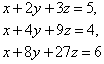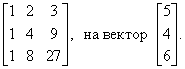АЛГЕБРА АБСТРАКТНАЯ
АЛГЕБРА АБСТРАКТНАЯ (общая алгебра), раздел современной математики, выросший из исследования уравнений и теории чисел. Свою теперешнюю форму абстрактная алгебра начала приобретать лишь в двадцатом веке. Занимается главным образом изучением систем, элементы которых можно сочетать по различным правилам, получая в результате новые элементы, вне зависимости от конкретной природы самих элементов. В последние десятилетия абстрактная алгебра все глубже проникает в различные разделы математики, становясь неоценимым средством исследования в столь различных ее областях, как геометрия, топология, математический анализ и дифференциальные уравнения. Даже у социологов и аналитиков, работающих в сфере бизнеса, возникает необходимость в хотя бы поверхностном знакомстве с теорией матриц, являющейся частью абстрактной алгебры. Фактически в настоящее время сложилась такая ситуация, что наиболее важными являются не те достижения абстрактной алгебры, которые способствуют углублению наших знаний в самой этой области, а те, что предлагают новые средства исследования для других ветвей математики.
Абстрактная алгебра оказалась полезной не только в математике. Ее средства и методы используются всюду, где возникает потребность в организации больших объемов данных. Абстрактная алгебра нашла применение при решении широкого круга проблем – от проектирования электронных схем до составления суточных графиков работы нефтеперегонных заводов, позволяющих максимизировать прибыль. Кратко остановимся на некоторых основных алгебраических системах.
Группы.
Группой G называется множество, или набор, элементов a, b, ... (относительно их природы не делается никаких предположений), в котором задана операция, ставящая в соответствие каждой паре элементов a, b из G третий элемент, ab, называемый их произведением, причем
(i) (ab) c = a (bc), т.е. произведение элемента ab и еще одного элемента c из G равно произведению элементов a и bc;
(ii) для любой пары элементов a, b из G существуют элементы x и y из G, такие, что xa = b, ay = b.
(Такая операция обычно называется умножением.) Следует заметить, что условие (ii) означает возможность деления в группе. Действительно, в силу условий (i) и (ii) в G всегда существует такой элемент 1 (называемый единицей или единичным элементом), что 1a = a1 = a для всех элементов a группы G, и для каждого элемента a из G в G существует элемент 1/a, называемый его обратным, такой, что a (1/a) = (1/a) a = 1. Тогда мы можем записать x = b (1/a), y = (1/a) b. Различать элементы x и y необходимо, поскольку не предполагалось, что ab = ba. Следует ясно сознавать, что слова «умножение» и «деление» используются в теории групп просто для операции, ставящей в соответствие двум элементам a и b исходного множества третий элемент той же группы, для которого с тем же успехом можно было бы использовать символы a * b, a + b или a Щ b.
Таким образом, для того чтобы задать конкретную группу, нужно указать множество ее элементов, определить на нем операцию умножения и, наконец, проверить, что введенное умножение удовлетворяет условиям (i) и (ii). Приведем несколько примеров групп.
(A) Множество всех положительных и отрицательных целых чисел, включая нуль,..., -3, -2, -1, 0, 1, 2, 3,..., где в качестве произведения двух чисел берется их обычная сумма. Условие (i) – просто закон ассоциативности сложения a + (b + c) = (a + b) + c; что касается условия (ii), то можно положить x = y = b – a.
(B) Множество всех отличных от нуля рациональных чисел (дробей p/q, где p и q – положительные или отрицательные целые числа) с произведением, определенным, как обычно: (p/q)(pў/qў) = ppў/qqў. Условие (i), как и в предыдущем примере, – это одно из основных свойств чисел, а условие (ii) удовлетворяется, если для a = p/q, b = pў/qў положить x = y = b : a = pўq/qўp.
(C) Более абстрактным примером может служить так называемая циклическая группа порядка n: множество ее элементов составляют n символов a0, a1, a2,..., an – 1, а произведение определяется соотношением akal = ar, где r = k + l, если k + l < n; если же k + l і n, то r – остаток от деления числа k + l на n. Условия (i) и (ii) проверяются без труда, a0 играет роль единичного элемента, а 1/ak = an – k.
В этих трех примерах умножение коммутативно, т.е. ab = ba. Группы с таким умножением называются коммутативными или абелевыми в честь Н.Абеля (1802–1829).
(D) Пусть H – множество всех вращений плоскости вокруг некоторой неподвижной точки P, а также ее отражений относительно заданной прямой l, проходящей через P. Если a и b – два элемента из H, то под ab условимся понимать преобразование плоскости, получаемое при выполнении сначала преобразования b, а затем преобразования a. Взяв все возможные произведения элементов из H, мы получим группу G, называемую двумерной ортогональной группой. Слово «ортогональная» в названии группы указывает на то, что преобразования из G сохраняют прямые углы. Нетрудно видеть, что условие (i) выполняется; что же касается условия (ii), то если определить 1/a для любого элемента a из G как преобразование, которое уничтожает действие преобразования a, то x = (1/a) b, y = b (1/a) будут удовлетворять условию (ii). Эта группа неабелева. Действительно, пусть a – поворот на 45° вокруг точки P, а b – отражение относительно заданной прямой. Рассматривая, что произойдет с произвольно выбранной точкой, не лежащей на этой прямой, нетрудно убедиться, что ab № ba.
(E) Наш последний пример – так называемая симметрическая группа, Sn, n-й степени. Это множество всех подстановок на n символах 1, 2, 3,..., n. В данном случае подстановка – это замена каждого целого числа i от 1 до n другим числом, f(i), также заключенным между 1 и n, причем так, что f(i) № f(j), если i № j. Под fЧg здесь понимается подстановка, которая получается при выполнении сначала подстановки g, а затем подстановки f. Условия (i) и (ii) проверяются так же, как мы проверяли их в примере (D). При n > 2 группа Sn неабелева. Например, в S3, если f и g заданы соотношениями f (1) = 2, f (2) = 3, f(3) = 1, g(1) = 3, g(2) = 2, g(3) = 1, то (fg)(1) = f(g(1)) = f(3) = 1, но (gf) (1) = g(2) = 2; поэтому fg № gf.
Одна из основных задач теории групп – более явное описание структуры некоторых классов групп. Как показывают приведенные примеры, существует огромное количество самых разных типов групп: группы бывают конечные ((C) и (E)) и бесконечные ((A), (B) и (D)), абелевы и неабелевы, и можно указать еще множество других типов, отличающихся во многих важных отношениях. Таким образом, нужно доказывать утверждения типа: «если группа G удовлетворяет некоторым предположениям, она должна выглядеть таким-то и таким-то образом». Примером таких утверждений является следующая теорема: любая абелева группа, состоящая из конечного числа n элементов, где n – простое число, является циклической группой порядка n.
Теория групп находит применение почти во всех разделах математики, играя роль связующего звена между многими, на первый взгляд совсем разными, ее областями. Пример групп (D) показывает, что эта теория очень полезна при рассмотрении геометрических задач, но она оказывает неоценимую помощь и в чисто аналитических разделах математики. Все шире используют теорию групп в своей работе и физики-теоретики. Чтобы еще раз продемонстрировать, как используется теория групп в геометрии, отметим, что различные геометрии (евклидова, гиперболическая, эллиптическая и т.д.) на плоскости можно охарактеризовать их группами движений. Иначе говоря, эти группы различаются своей структурой, и все геометрические факты допускают переформулировку в виде чисто теоретико-групповых теорем. Группы имеют также очень важное значение в топологии – разделе геометрии, изучающем общие соотношения формы и пространства, не обращая внимания на метрические характеристики размера. Например, топологическая задача о том, сколькими способами одна резиновая сфера может быть обернута вокруг другой, сводится к вычислению некоторых групп – так называемых гомотопических групп.
Кольца.
Множество R элементов a, b, c, ... называется кольцом, если каждой паре элементов a, b из R поставлен в соответствие некоторый элемент из R, называемый их суммой и обозначаемый a + b, и еще один элемент из R, называемый их произведением и обозначаемый ab. Кроме того, должны выполняться следующие условия:
(1) a + (b + c) = (a + b) + c;
(2) a + b = b + a;
(3) для любых двух элементов a, b из R существует элемент x из R, такой, что a + x = b;
(4) (ab) c = a (bc);
(5) a (b + c) = ab + ac, (b + c) a = ba + ca.
Внимательный читатель заметит, что выполнение условий (1), (2) и (3) означает, что R – абелева группа по сложению. Единственный элемент x, такой, что a + x = a (существование которого может быть доказано), называется нулевым элементом кольца R и обозначается 0. Исходя из свойств (1)–(5), нетрудно доказать, что для каждого элемента a из кольца R справедливо равенство aЧ0 = 0Чa = 0. Однако есть кольца, в которых нулем может оказаться произведение ненулевых элементов, т.е. в таких кольцах существуют элементы a, b, ни один из которых не равен 0, но для которых ab = 0. Такие кольца называются кольцами с делителями нуля. (Мы встретимся с ними в разделах, посвященных полям и матрицам.) Многие тождества, известные из обычной алгебры, выполняются и в произвольных кольцах: все обычные тождества, содержащие только сложение и вычитание, а также тождества, не использующие коммутативность умножения или возможность деления, сохраняют силу и в произвольном кольце R. Например, тождество a [(b + c) + (e + f)] = (ae + ac) + (ab + af) остается верным в любом кольце R.
Примерами колец могут служить уже упоминавшееся множество всех целых чисел с обычными операциями сложения и умножения и множество всех многочленов f (x) = a0 + a1x +... + anxn, где ai – действительные числа, а x – переменная. Два многочлена являются одним и тем же элементом кольца в том и только в том случае, когда коэффициенты при одинаковых степенях переменной x равны. Сумма многочленов
определяется так:
а их произведение – так:
где cj = a0bj + a1bj – 1 +... + aj – 1b1 + ajb0. Проверка пяти условий из определения кольца – занятие утомительное, но не сопряженное с какими-либо реальными трудностями. Она опирается на тот факт, что эти условия выполняются для действительных чисел. В обоих примерах умножение коммутативно (т.е. ab = ba), и оба эти кольца не содержат делителей нуля. Пример некоммутативного кольца с делителями нуля мы приведем в заключительном разделе.
Как и в случае групп, хотелось бы описать кольца более полно. Эта проблема частично решена, и мы вернемся к ней чуть позже. Коммутативные кольца без делителей нуля типа приведенных выше встречаются в различных теоретико-числовых проблемах, и существует хорошо разработанная теория колец этого класса.
Самой знаменитой теоретико-числовой проблемой, немало способствовавшей развитию теории колец, по праву следует считать так называемую великую теорему Ферма: «Если n – натуральное число, большее двух, то не существует таких отличных от нуля целых чисел x, y, z, что xn + yn = zn». (На полях своего экземпляра Арифметики Диофанта П.Ферма сформулировал эту теорему, отметив, что нашел ее «поистине чудесное доказательство», но не привел его.) К настоящему времени эта теорема доказана, но не элементарными методами, которые могли быть доступны Ферма, а с помощью теории эллиптических кривых. Однако значительная часть теории колец возникла в результате попыток доказать теорему Ферма. В частности, эти попытки привели к введению понятия идеала. Подкольцо S кольца R (т.е. некоторое подмножество элементов кольца R, такое, что разность и произведение любых двух элементов из S суть снова элементы из S) называется идеалом кольца R, если для каждого элемента s из S и каждого элемента r из R оба произведения rs и sr принадлежат S. Поскольку подробное изложение теории идеалов увело бы нас далеко в сторону от цели статьи, упомянем лишь, что в коммутативных кольцах некоторые типы идеалов играют такую же роль, как простые числа в кольце целых чисел, и что такие геометрические объекты, как алгебраические кривые на плоскости, могут быть полностью описаны идеалами в кольце многочленов от двух переменных.
При проектировании электронных схем очень полезными оказываются кольца R, каждый элемент r которых удовлетворяет соотношению r2 = r. Вычисления в рамках таких «булевых колец» в точности соответствуют некоторым правилам проектирования схем, так что задача построения схемы, удовлетворяющей заданным условиям, сводится к более простой задаче упрощения соответствующего выражения в булевом кольце.
Поля.
Полем F называется коммутативное кольцо, в котором ненулевые элементы образуют абелеву группу по умножению. Это означает, что над элементами поля все четыре рациональные операции (сложение, вычитание, умножение и деление на ненулевые элементы) могут проводиться так же, как над обычными числами, и что для полей остаются в силе все правила элементарной алгебры. Приведем несколько примеров полей.
Множество всех действительных чисел с обычными операциями сложения, вычитания, умножения и деления.
Множество всех комплексных чисел (всех чисел вида a + bi, где a и b – действительные числа и i2 = –1) также дает пример поля. Четыре рациональные операции в этом случае определяются следующим образом:
Нетрудно проверить, что все условия из определения поля при таком задании операций на указанном множестве выполняются.
Еще один пример поля – множество всех чисел вида ![]() , где a, b – рациональные числа, с операциями сложения, вычитания, умножения и деления, очень похожими на операции, введенные на множестве комплексных чисел в предыдущем примере, с той разницей, что i заменяется на
, где a, b – рациональные числа, с операциями сложения, вычитания, умножения и деления, очень похожими на операции, введенные на множестве комплексных чисел в предыдущем примере, с той разницей, что i заменяется на ![]() , а равенство i2 = –1 – на равенство
, а равенство i2 = –1 – на равенство ![]() .
.
Более удивительный пример поля получается следующим образом. Любое целое число при делении на 3 дает один из остатков 0, 1, 2. Разделим множество всех целых чисел на три класса так, чтобы все числа, принадлежащие к одному классу, давали при делении на 3 один и тот же остаток. Обозначим эти классы через {0}, {1} и {2}. Тогда число 9 попадает в класс {0}, число 185 – в класс {2}, а число 73 – в класс {1}. Определим сложение и умножение двух классов следующим образом: из каждого класса выберем по одному представителю, произведем сложение или умножение представителей и в качестве результата возьмем класс, которому принадлежит соответственно сумма или произведение представителей (можно проверить, что полученный класс не зависит от выбора представителей и что класс {0} играет роль нулевого элемента). Например, {2} + {2} = {1}, {0} + {1} = {1}, {2}Ч{2} = {1} и {1}Ч{2} = {2}. Те же соображения остаются в силе, если вместо числа 3 мы выберем любое целое число m. Однако поле мы получим только в том случае, когда число m простое (т.е. делится только на себя и на 1). Причина этого очевидна: в поле всегда отсутствуют делители нуля, ибо если ab = 0, но при этом a № 0, то 0 = (1/a)(ab) = b, так как в поле всегда существует элемент 1/a, хотя его, разумеется, может не быть в кольце. Таким образом, в любом поле произведение ab может быть равно нулю только в том случае, когда a или b равно нулю. Если m = m1m2, где m1№ m, m2№ m, то {m1} № 0, {m2} № 0, но {m1m2} = 0 (так как m1m2 дает при делении на m остаток 0). Таким образом, мы можем ожидать, что получится поле – и всегда в действительности получаем поле – только в том случае, когда m – простое число (см. также ЧИСЕЛ ТЕОРИЯ).
Последний пример – поле всех рациональных функций одной переменной, т.е. множество всех отношений многочленов (a0 + a1x +... + anxn) ё (b0 + b1x +... + bmxm) при обычном определении операций сложения и умножения. Это поле имеет очевидную связь с упоминавшимся выше кольцом многочленов и получается из него взятием всех формальных отношений. Разумеется, аналогичным образом из кольца целых чисел получается поле всех рациональных чисел. Для всех коммутативных колец R без делителей нуля ситуация здесь общая. Мы всегда можем построить поле F формальных отношений элементов кольца R, в котором само R будет содержаться как множество всех элементов вида a ё 1.
В отличие от ситуации с группами и кольцами мы располагаем довольно полным описанием всех возможных полей. Этим описанием мы обязаны, главным образом, Э.Штейницу (1871–1928). Приведенные выше примеры иллюстрируют все возможные типы полей. Разумеется, и в теории полей осталось еще много нерешенных проблем, однако они значительно тоньше, чем простое описание.
Поля важную роль играют при исследовании алгебраических уравнений. Пусть
– уравнение относительно x с коэффициентами из некоторого поля F. Может случиться так, что ни один элемент из F при подстановке вместо x не обращает левую часть формулы (*) в нуль. Однако можно доказать, что всегда существует более широкое поле Fў, содержащее F, такое, что один из его элементов обращает левую часть (*) в нуль. Этот элемент называется корнем уравнения (*). Например, пусть F – поле рациональных чисел и x2 – 2 = 0 – уравнение, которое требуется решить. Тогда в F не существует корня этого уравнения, но поле из третьего примера содержит такой корень, а именно число ![]() , и содержит поле F как множество всех элементов вида
, и содержит поле F как множество всех элементов вида ![]() . Возвращаясь к общему случаю, заметим, что всегда можно найти еще более широкое поле FІ, которое содержит все корни уравнения (*) и является наименьшим из полей, обладающих этим свойством. Изучением взаимосвязи между F и FІ занимается теория Галуа, названная так в честь Э.Галуа (1811–1832). Лучше всего эта взаимосвязь выражается в терминах некоторых групп, что может служить ярким примером взаимопроникновения двух разделов алгебры. Галуа построил свою теорию в связи с исследованием следующей задачи. Давно было известно, что корни уравнения (*) первой, второй, третьей и четвертой степеней (т.е. корни уравнений a0 + a1x = 0, a0 + a1x + a2x2 = 0, a0 + a1x + a2x2 + a3x3 = 0, a0 + a1x + a2x2 + a3x3 + a4x4 = 0) могут быть явно выражены через коэффициенты ai; например, для уравнений второй степени корни имеют вид
. Возвращаясь к общему случаю, заметим, что всегда можно найти еще более широкое поле FІ, которое содержит все корни уравнения (*) и является наименьшим из полей, обладающих этим свойством. Изучением взаимосвязи между F и FІ занимается теория Галуа, названная так в честь Э.Галуа (1811–1832). Лучше всего эта взаимосвязь выражается в терминах некоторых групп, что может служить ярким примером взаимопроникновения двух разделов алгебры. Галуа построил свою теорию в связи с исследованием следующей задачи. Давно было известно, что корни уравнения (*) первой, второй, третьей и четвертой степеней (т.е. корни уравнений a0 + a1x = 0, a0 + a1x + a2x2 = 0, a0 + a1x + a2x2 + a3x3 = 0, a0 + a1x + a2x2 + a3x3 + a4x4 = 0) могут быть явно выражены через коэффициенты ai; например, для уравнений второй степени корни имеют вид
Естественно, что делались попытки вывести аналогичные формулы для корней уравнений пятой и более высоких степеней. Н.Абелю в 1824 удалось показать, что для общего (т.е. с буквенными коэффициентами) уравнения пятой и более высоких степеней такой формулы не существует, т.е. что общее уравнение степени n і 5 неразрешимо в радикалах. После этого встал вопрос об условиях, которым должны удовлетворять коэффициенты уравнения, чтобы оно было разрешимо в радикалах. Ответ на этот вопрос был найден Галуа. В частности, согласно теории Галуа, неразрешимость в радикалах общего уравнения степени n, n і 5, связана со строением группы Sn (определенной нами ранее).
Теория полей сыграла выдающуюся роль в доказательстве неразрешимости трех знаменитых проблем древности: удвоения куба, квадратуры круга и трисекции угла.
Наконец, упомянем о том, что для любого поля F всегда существует поле F0, которое содержит все корни всех уравнений вида (*) с коэффициентами из F при всех возможных n. Если F – поле действительных или комплексных чисел, то F0 – поле комплексных чисел (наш второй пример). Эту теорему часто называют основной теоремой алгебры. Она имеет иную, эквивалентную, формулировку: любой многочлен с комплексными коэффициентами имеет корень в поле комплексных чисел. Доказательства этой теоремы давали многие известные математики (включая Эйлера и Лапласа), но К.Гаусс (1777–1855) первым доказал ее совершенно строго, без предварительного предположения о существовании корней многочлена.
Векторы и матрицы.
Знакомые всем физические векторы, используемые для представления объектов, характеризуемых величиной и направлением (наглядно их изображают символами со стрелкой), можно рассматривать и на более абстрактном уровне. Такой подход позволяет понять более сложные операции над векторами, распространить векторную алгебру на случай n-мерного пространства и расширить область применения понятия «вектор».
Пусть F – поле. Строка (a1, a2,..., an) или столбец
из n элементов называется n-мерным вектором-строкой или n-мерным вектором-столбцом v. Два n-мерных вектора-строки v, vў равны в том и только в том случае, если равны все их соответствующие элементы. Векторы можно складывать и вычитать по правилу (a1,..., an) ± (b1,..., bn) = (a1± b1,..., an ± bn). Нетрудно проверить, что при таких определениях векторы образуют абелеву группу. Важное значение имеет еще одна операция над векторами: если v = (a1,..., an) – вектор, а a – элемент из F, то по определению av = (aa1, aa2,..., aan). Векторы допускают и более абстрактное определение, которое, как можно показать, эквивалентно приведенному выше и существенно увеличивает применимость векторов в различных областях науки.
Можно определить произведение двух векторов-строк, но гораздо полезнее следующее определение произведения n-мерного вектора-строки на n-мерный вектор-столбец:
Следует заметить, что такое произведение будет уже не вектором, а просто элементом из F.
Матрицей A размера n ґ n называется множество n-мерных векторов-строк, записанных один под другим (или n-мерных векторов-столбцов, записанных рядом). Например,
Две матрицы A и Aў равны в том и только в том случае, когда у них равны все элементы, стоящие на одинаковых местах. Сумма двух матриц размера n ґ n по определению получается сложением соответствующих векторов-строк, а произведение AAў определяется по следующему правилу: в качестве j-го элемента i-й строки берется произведение i-й строки матрицы A на j-й столбец матрицы Aў. Например, при n = 2 и
имеем
и
Нетрудно проверить, что при таких определениях множество матриц размера nґn образует кольцо. Это кольцо некоммутативно и имеет делители нуля, как показывает следующий пример:
так как нулевым элементом кольца матриц 2 ґ 2 служит матрица
Кольцо матриц размера n ґ n с элементами из некоммутативного поля (системы, обладающей всеми свойствами поля за исключением коммутативности умножения и называемой телом) допускает более абстрактное представление. Точнее говоря, справедлива теорема, которая утверждает, что любое кольцо, удовлетворяющее некоторым двум условиям, обязательно должно быть множеством матриц размера n ґ n над некоторым телом. Эту теорему можно даже несколько усилить и тем самым получить описание более широкого класса колец.
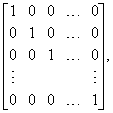
Для некоторых матриц A существуют обратные матрицы; это означает, что для матрицы A существует матрица Aў, такая, что AAў = AўA = I, где I – единичная матрица
которая обладает тем свойством, что для любой матрицы B справедливо соотношение IB = BI = B. Множество всех таких матриц размера n ґ n образует группу, и это обстоятельство имеет важное значение для изучения более абстрактных групп, поскольку большой их класс допускает матричное представление.
Векторы и матрицы находят все более широкое применение и вне математики. Они были изобретены в середине 19 в. в связи с изучением n-мерной геометрии. С тех пор их стали использовать везде, где приходится иметь дело с обработкой больших массивов данных. С использованием матриц решаются многие технические задачи, связанные с расчетом напряжений, деформаций, колебаний. Решение системы линейных уравнений с несколькими переменными по существу является задачей матричного исчисления. Например, систему уравнений
можно записать в виде
и затем, чтобы найти x, y, z, нужно умножить матрицу, обратную матрице
Матрицы используются и при решении систем дифференциальных уравнений, которые возникают в большинстве наук: такую систему можно заменить одним матричным дифференциальным уравнением.
Одно из главных применений матриц в общественных науках связано с построением моделей различных ситуаций. Например, экономическую ситуацию в стране часто моделируют с помощью матрицы с примерно 100 строками и столбцами. На основании операций над такой матрицей экономисты создают свои прогнозы. Пример использования матриц в деловом мире – линейное программирование, которое можно использовать при составлении производственных планов, схем распределения сырья и готовой продукции и в других сложных операциях. Не вдаваясь в подробности, можно сказать, что линейная программа состоит из очень большого числа утверждений о взаимосвязях между различными факторами, которые необходимо учесть перед тем, как принять окончательное решение. Эти утверждения сводятся в некоторую матрицу, операции над которой позволяют программисту решить, какая из нескольких имеющихся процедур оптимальна для решения рассматриваемой проблемы. Это позволяет найти процедуру, обеспечивающую максимальную прибыль или максимальную экономию времени.
Калужник Л.А. Введение в общую алгебру. М., 1973
Фрид Э. Элементарное введение в абстрактную алгебру. М., 1979
Общая алгебра (под ред. Л.А.Скорнякова), тт. 1–2. М., 1990
Ответь на вопросы викторины «Математика»