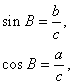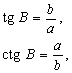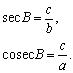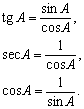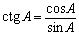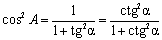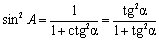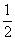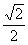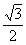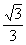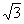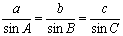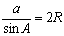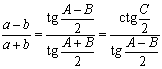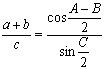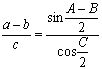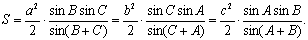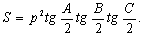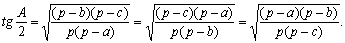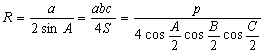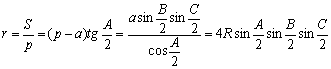ТРИГОНОМЕТРИЯ
ТРИГОНОМЕТРИЯ – (от греч. trigwnon – треугольник и metrew – измеряю) – математическая дисциплина, изучающая зависимости между углами и сторонами треугольников и тригонометрические функции.
Термин «тригонометрия» ввел в употребление в 1595 немецкий математик и богослов Варфоломей Питиск, автор учебника по тригонометрии и тригонометрических таблиц. К концу 16 в. большинство тригонометрических функций было уже известно, хотя само это понятия еще не существовало.
В тригонометрии выделяют три вида соотношений: 1) между самими тригонометрическими функциями; 2) между элементами плоского треугольника (тригонометрия на плоскости); 3) между элементами сферического треугольника, т.е. фигуры, высекаемой на сфере тремя плоскостями, проходящими через ее центр. Тригонометрия началась именно с наиболее сложной, сферической части. Она возникла прежде всего из практических нужд. Древние наблюдали за движением небесных светил. Ученые обрабатывали данные измерений, чтобы вести календарь и правильно определять время начала сева и сбора урожая, даты религиозных праздников. По звездам вычисляли местонахождение корабля в море или направление движения каравана в пустыне. Наблюдения за звездным небом с незапамятных времен вели и астрологи.
Естественно, все измерения, связанные с расположением светил на небосводе, – измерения косвенные. Прямые могли быть проведены только на поверхности Земли, но и здесь далеко не всегда удавалось непосредственно определить расстояние между какими-то пунктами и тогда вновь прибегали к косвенным измерениям. Например, вычисляли высоту дерева, сравнивая длину его тени с длиной тени от какого-нибудь шеста, высота которого была известна. Аналогичным образом вычисляли и размеры острова в море. Подобные задачи сводятся к анализу треугольника, в котором одни его элементы выражают через другие. Этим и занимается тригонометрия. А поскольку звезды и планеты представлялись древним точками на небесной сфере, то сначала стала развиваться именно сферическая тригонометрия. Ее считали разделом астрономии.
А начиналось все очень давно. Первые отрывочные сведения по тригонометрии сохранились на клинописных табличках Древнего Вавилона. Астрономы Междуречья научились предсказывать положение Земли и Солнца и именно от них к нам пришла система измерения углов в градусах, минутах и секундах, потому что у вавилонян была принята шестидесятеричная система счисления.
Однако первые по-настоящему важные достижения принадлежат древнегреческим ученым. Например, 12-я и 13-я теоремы второй книги Начал Евклида (конец 4–3 в. до н. э.) выражают по существу теорему косинусов. Во 2 в. до н.э. астроном Гиппарх из Никеи (180–125 до н.э.) составил таблицу для определения соотношений между элементами треугольников. Такие таблицы нужны потому, что значения тригонометрических функций нельзя вычислить по аргументам с помощью арифметических операций. Тригонометрические функции приходилось рассчитывать заранее и хранить в виде таблиц. Гиппарх подсчитал в круге заданного радиуса длины хорд, отвечающих всем углам от 0 до 180°, кратным 7,5°. По существу, это таблица синусов. Труды Гиппарха до нас не дошли, но многие сведения из них включены в Альмагест (II в.) – знаменитое сочинение в 13 книгах греческого астронома и математика Клавдия Птолемея (ум. ок.160 н. э.). Древние греки не знали синусов, косинусов и тангенсов, вместо таблиц этих величин они употребляли таблицы, позволявшие находить хорду окружности по стягиваемой дуге. В Альмагесте автор приводит таблицу длин хорд окружности радиуса в 60 единиц, вычисленных с шагом 0,5° с точностью до 1/3600 единицы, и объясняет, как эта таблица составлялась. Труд Птолемея несколько веков служил введением в тригонометрию для астрономов.
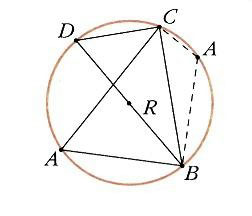
Чтобы понять, как ученые древности составляли тригонометрические таблицы, надо познакомиться с методом Птолемея. Метод основан на теореме – произведение диагоналей вписанного в окружность четырехугольника равно сумме произведений его противоположных сторон.
Пусть ABCD – вписанный четырехугольник, АD – диаметр окружности, а точка O – ее центр (рис. 1). Если известно, как вычислять хорды, стягивающие углы DOC = a и DОВ = b, т. е. сторону СD и диагональ B, то, по теореме Пифагора, из прямоугольных треугольников АDВ и АDС можно найти АВ и АС, а потом, по теореме Птолемея, – BC = (АС·ВD – АВ·СD) /АD, т.е. хорду, стягивающую угол ВОС = b – a. Некоторые хорды, например стороны квадрата, правильных шестиугольника и восьмиугольника, отвечающие углам 90, 60 и 45°, легко определить. Известна также сторона правильного пятиугольника, которая стягивает дугу в 72°. Приведенное выше правило позволяет вычислять хорды для разностей этих углов, например для 12° = 72° – 60°. Кроме того, можно находить хорды половинных углов, однако этого недостаточно, чтобы рассчитать, чему равна хорда дуги в 1°, – хотя бы потому, что все названные углы кратны 3°. Для хорды 1° Птолемей нашел оценку, показав, что она больше 2/3 хорды (3/2)° и меньше 4/3 хорды (3/4)° – двух чисел, совпадающих с достаточной для его таблиц точностью.
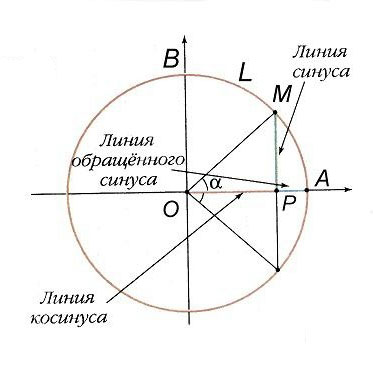
Если греки по углам вычисляли хорды, то индийские астрономы в сочинениях 4–5 вв. перешли к полухордам двойной дуги, т.е. в точности к линиям синуса (рис. 2). Они пользовались и линиями косинуса – вернее, не его самого, а «обращенного» синуса, получившего позднее в Европе название «синус-верзус», сейчас эта функция, равная 1 – cos a, уже не употребляется. Впоследствии тот же подход привел к определению тригонометрических функций через отношения сторон прямоугольного треугольника.
За единицу измерения отрезков MP, OP, PA принималась дуговая минута. Так, линия синуса дуги AB = 90° есть OB – радиус окружности; дуга AL, равная радиусу, содержит (округленно) 57°18' = 3438'.
Дошедшие до нас индийские таблицы синусов (древнейшая составлена в 4–5 веке н.э.) не столь точны, как птолемеевы; они составлены через 3°45' (т.е. через 1/24 часть дуги квадранта).
Термины «синус» и «косинус» пришли от индийцев, не обошлось и без любопытного недоразумения. Полухорду индийцы называли «ардхаджива» (в переводе с санскрита – «половина тетивы лука»), а потом сократили это слово до «джива». Мусульманские астрономы и математики, получившие знания по тригонометрии от индийцев, восприняли его как «джиба», а затем оно превратилось в «джайб», что на арабском языке означает «выпуклость», «пазуха». Наконец, в 7 в. «джайб» буквально перевели на латынь словом «sinus», которое не имело никакого отношения к обозначаемому им понятию. Санскритское «котиджива» – синус остатка (до 90°), а на латинском – sinus complementi, т.е. синус дополнения, в 17 в. сократилось до слова «косинус». Наименования «тангенс» и «секанс» (в переводе с латинского означающие «касательная» и «секущая») введены в 1583 немецким ученым Финком.
Большой вклад в развитие тригонометрии внесли арабские ученые, например, Аль-Баттани (ок. 900 н.э.). В 10 в. багдадский ученый Мухаммед из Буджана, известный под именем Абу-ль-Вефа (940–997), присоединил к линиям синусов и косинусов линии тангенсов, котангенсов, секансов и косекансов. Он дает им те же определения, которые содержатся и в наших учебниках. Абу-ль-Вефа устанавливает и основные соотношения между этими линиями.
Итак, к концу 10 в. ученые исламского мира уже оперировали, наряду с синусом и косинусом, четырьмя другими функциями – тангенсом, котангенсом, секансом и косекансом; открыли и доказали несколько важных теорем плоской и сферической тригонометрии; использовали окружность единичного радиуса (что позволило толковать тригонометрические функции в современном смысле); придумали полярный треугольник сферического треугольника. Арабские математики составили точные таблицы, например таблицы синусов и тангенсов с шагом в 1' и точностью до 1/700 000 000. Очень важной прикладной задачей была и такая: научиться определять направление на Мекку для пяти ежедневных молитв, где бы ни находился мусульманин.
Особенно большое влияние на развитие тригонометрии оказал Трактат о полном четырехстороннике астронома Насир-эд-Дин из Туса (1201–1274), известного так же под именем ат-Туси. Это было первое в мире сочинение, в котором тригонометрия трактовалась как самостоятельная область математики.
В 12 в. был переведен с арабского языка на латинский ряд астрономических работ, по ним впервые европейцы познакомились с тригонометрией.
Трактат Насир-эд-Дина произвел большое впечатление на немецкого астронома и математика Иоганна Мюллера (1436–1476). Современники больше знали его под именем Региомонтана (так переводится на латинский название его родного города Кенигсберга, ныне – Калининграда). Региомонтан составил обширные таблицы синусов (через 1 минуту с точностью до седьмой значащей цифры). Он впервые отступил от шестидесятиричного деления радиуса и за единицу измерения линии синуса принял одну десятимиллионную часть радиуса. Таким образом, синусы выражались целыми числами, а не шестидесятиричными дробями. До введения десятичных дробей оставался только один шаг, но он потребовал более 100 лет. Труд Региомонтана О треугольниках всех родов пять книг сыграл в европейской математике ту же роль, что и сочинение Насир-эд-Дина в науке мусульманских стран.
За таблицами Региомонтана последовал ряд других, еще более подробных. Друг Коперника Ретик (1514–1576) вместе с несколькими помощниками в течение 30 лет работал над таблицами, законченными и изданными в1596 его учеником Отто. Углы шли через 10'', а радиус делился на 1 000 000 000 000 000 частей, так что синусы имели 15 верных цифр.
Дальнейшее развитие тригонометрии шло по пути накопления и систематизации формул, уточнения основных понятий, становления терминологии и обозначений. Многие европейские математики работали в области тригонометрии. Среди них такие великие ученые, как Николай Коперник (1473–1543), Тихо Браге (1546–1601) и Иоганн Кеплер (1571–1630). Франсуа Виет (1540–1603) дополнил и систематизировал различные случаи решения плоских и сферических треугольников, открыл «плоскую» теорему косинусов и формулы для тригонометрических функций от кратных углов. Исаак Ньютон (1643–1727) разложил эти функции в ряды и открыл путь для их использования в математическом анализе. Леонард Эйлер (1707–1783) ввел и само понятие функции, и принятую в наши дни символику. Величины sin x, cos x и т.д. он рассматривал как функции числа x – радианной меры соответствующего угла. Эйлер давал числу x всевозможные значения: положительные, отрицательные и даже комплексные. Он также обнаружил связь между тригонометрическими функциями и экспонентой комплексного аргумента, что позволило превратить многочисленные и зачастую весьма замысловатые тригонометрические формулы в простые следствия из правил сложения и умножения комплексных чисел. Он же ввел и обратные тригонометрические функции.
К концу 18 в. тригонометрия как наука уже сложилась. Тригонометрические функции нашли применение в математическом анализе, физике, химии, технике – везде, где приходится иметь дело с периодическими процессами и колебаниями – будь то акустика, оптика или качание маятника.
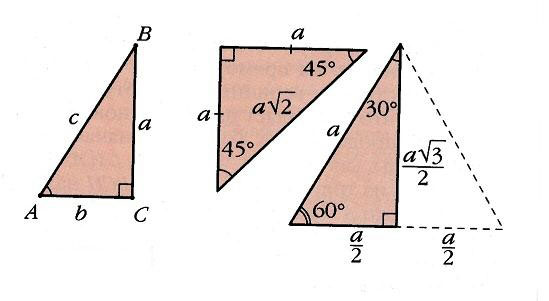
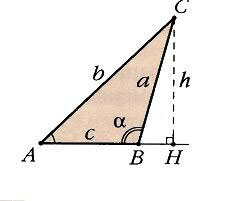
Решение любых треугольников, в конечном счете, сводится к решению прямоугольных треугольников (т.е. таких, у которых один из углов – прямой). Поскольку все прямоугольные треугольники с заданным острым углом подобны друг другу, отношения их соответственных сторон одинаковы. Например, в прямоугольном треугольнике ABC отношение двух его сторон, например, катета а к гипотенузе с, зависит от величины одного из острых углов, например А. Отношения различных пар сторон прямоугольного треугольника и называются тригонометрическими функциями его острого угла. Всего таких отношений в треугольнике шесть, и им отвечают шесть тригонометрических функций (обозначения сторон и углов треугольника на рис. 3).
Синус 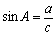 (отношение противолежащего катета к гипотенузе),
(отношение противолежащего катета к гипотенузе),
косинус 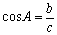 (отношение прилежащего катета к гипотенузе),
(отношение прилежащего катета к гипотенузе),
тангенс 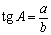 (отношение противолежащего катета к прилежащему),
(отношение противолежащего катета к прилежащему),
котангенс 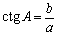 (отношение прилежащего катета к противолежащему),
(отношение прилежащего катета к противолежащему),
секанс sec A = 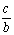 (отношение гипотенузы к прилежащему катету),
(отношение гипотенузы к прилежащему катету),
косеканс cosec A = 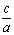 (отношение гипотенузы к противолежащему катету).
(отношение гипотенузы к противолежащему катету).
По отношению к углу B («дополнительному» углу по отношению к А) формулы меняются соответственно:
Так как А + В = 90°, то
sin A = cos B = cos (90° – A),
A = ctg B = ctg (90° – A).
Из определений вытекает несколько равенств, связывающих тригонометрические функции одного и того же угла между собой:
С учетом теоремы Пифагора a2 + b2 = c2 можно выразить все шесть функций через какую-нибудь одну.Например, синус и косинус связаны основным тригонометрическим тождеством
sin2A + cos2A = 1.
Некоторые соотношения между функциями:
tg A ctg A = 1,
Эти формулы справедливы и для тригонометрических функций любого угла, но ими надо пользоваться осторожно, поскольку правые и левые части могут иметь разные области определения.
Есть только два прямоугольных треугольника, у которых и углы «хорошие» (выражаются целым или рациональным числом градусов), и хотя бы одно из отношений сторон рационально. Это равнобедренный треугольник (с углами 45, 45 и 90°) и половина равностороннего треугольника (с углами 30, 60, 90°) – как раз те два случая, когда значения тригонометрических функций удается вычислить прямо по определению. Эти значения приведены в таблице
| n | 0 | 1 | 2 | 3 | 4 |
| Угол | 0 | 30° | 45° | 60° | 90° |
| sin |
0 |
1 |
|||
| cos |
1 |
0 |
|||
| tg |
0 |
1 |
– |
||
| ctg |
– |
1 |
0 |
 Для произвольного треугольника можно доказать теорему синусов:
Для произвольного треугольника можно доказать теорему синусов:
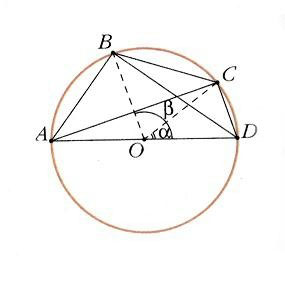
Отношения, входящие в теорему синусов, имеют простой геометрический смысл. Если описать окружность около треугольника ABC (рис. 4) и провести диаметр BD, то по теореме о вписанном угле РBCD = РA либо, если угол тупой, 180° – А. В любом случае a = BC = BD sin A = 2 R sin A или
где R – радиус описанной окружности треугольника АВС. Это «усиленная» теорема синусов, объясняющая, почему таблицы хорд древних были, по существу, таблицами синусов.
Доказывается и теорема косинусов
с2 = а2 + b2 – 2аb cos С.
позволяющая найти сторону треугольника по двум другим сторонам и углу между ними, а также углы по трем сторонам.
Есть и ряд других соотношений между элементами треугольника, например. теорема тангенсов:
называемая также формулой Региомонтана.
Формулы Мольвейде:
Из теорем синусов и косинусов можно вывести (с помощью тригонометрических тождеств) и другие формулы.
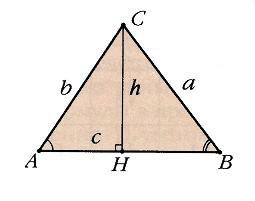
Поскольку площадь треугольника S = 1/2 aha = 1/2 bhb = 1/2 chc . Или
= 1/2 ab sin C = 1/2 bc sin A = 1/2 ca sin B;
Но с учетом формулы Герона:
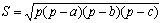 , где p – полупериметр треугольника,
, где p – полупериметр треугольника,
Для вычисления углов по заданным сторонам пользуются формулами:
Радиусы описанной и вписанной окружностей:
Можно вывести формулы сложения для синусов и косинусов
sin (a + b) = sin a cos b + cos a sin b.
sin (a – b) = sin a cos b – cos a sin b.
Именно эту формулу использовал Птолемей для составления своей таблицы хорд. (Теперь она называется теоремой Птолемея.) Аналогично можно написать формулы косинуса суммы и разности:
cos (a + b) = cos a cos b – sin a sin b,
cos (a – b) = cos a cos b + sin a sin b.
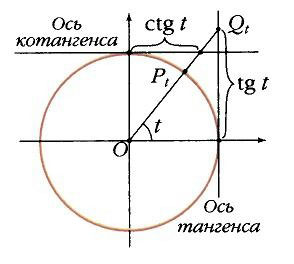
Общее определение тригонометрических функций
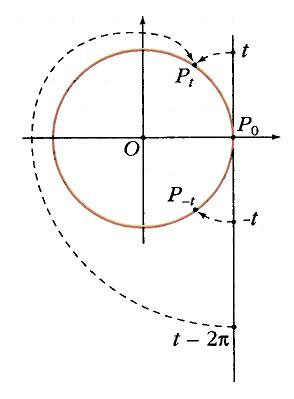
Пусть точка движется с единичной скоростью по единичной окружности с центром в начале координат О против часовой стрелки (рис. 5). В момент t = 0 точка минует P0 (1; 0). За время t точка проходит дугу длиной t и занимает положение Рt, а значит, угол, на который поворачивается луч, проведенный в эту точку из О, тоже равен t. Таким образом, мы сопоставляем каждому моменту времени, т.е. точке t действительной прямой, точку Рtединичной окружности.
Подобное отображение прямой на окружность иногда называют «намоткой». Если представить действительную ось в виде бесконечной нерастяжимой нити, приложить точку t = 0 к точке P0 окружности и начать наматывать оба конца нити на окружность, то каждая точка t попадет как раз в точку Рt. При этом:
1) точки оси, отстоящие друг от друга на целое число длин окружностей, т, е. на 2pk (k =±1, ± 2, …), попадают в одну и ту же точку окружности;
2) точки t и –t попадают в точки, симметричные относительно Ox;
3) при 0 Ј t Ј p угол P0OPtотложен в полуплоскость у і 0 и равен t (рис. 8).
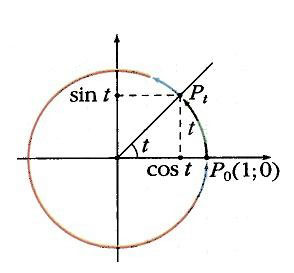
Три этих условия составляют формальное определение такого отображения – намотки. В силу условия 3 при 0 = t Ј p координаты точки р равны (cos t, sin t). Данное наблюдение и подсказывает определение: косинусом и синусом произвольного числа t называются соответственно абсцисса и ордината точки Рt.
Тангенс тоже можно определить через координаты. Проведем касательную к единичной окружности в точке (1; 0) (рис. 7). Она называется осью тангенсов. Точка Qt пересечения прямой OPt с осью тангенсов имеет координаты (1; sin t/cos t), и ее ордината, по определению, равна tg t. По абсолютной величине это длина отрезка касательной, проведенной из Qt к окружности. Таким образом, само название «тангенс» вполне оправдывается. Кстати, как и секанса: на рис. 9 sec t – отрезок OQt, являющийся, правда, не всей секущей, но ее частью. Наконец, котангенс можно определить как абсциссу точки пересечения OPt с осью котангенсов – касательной к единичной окружности в точке (0, 1): ctg t = cos t / sin t.
Теперь тригонометрические функции определены для всех чисел.
Марина Федосова
Колмогоров А.Н., Семенович А.Ф., Черкасов Р.С. Геометрия, М., 1981
Ответь на вопросы викторины «Математика»